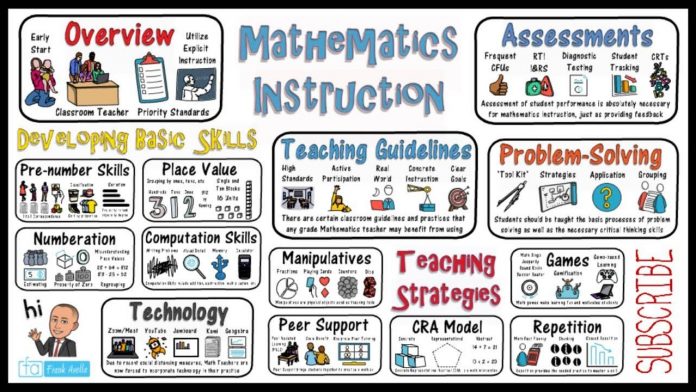
- 1. Use Formative Assessment to Guide Instruction
- 2. Employ Explicit Instruction for Key Concepts
- 3. Gamify Math Concepts to Boost Engagement
- 4. Mathematical Discourse with Structured Talk Moves
- 5. Apply Spaced Repetition and Interleaved Practice
- 6. Engage Students in Error Analysis to Build Conceptual Understanding
- 7. Use Manipulatives to Bridge Concrete and Abstract Thinking
- 8. Apply the Gradual Release of Responsibility Model (I Do, We Do, You Do)
- 9. Teach Problem-Solving with Polya’s Four-Step Process
- 10. Use Visual Representations to Enhance Comprehension
Do you find yourself re-explaining the same math concepts over and over, only for your students to struggle again the next day? Or maybe your class is a mix of abilities, and it’s hard to keep everyone on the same page? These are common challenges many teachers face when figuring out how to teach math in a way that truly sticks.
Math & ELA | PreK To Grade 5
Kids see fun.
You see real learning outcomes.
Watch your kids fall in love with math & reading through our scientifically designed curriculum.
Parents, try for free Teachers, use for free
In this guide, we’ll explore practical strategies that help students grasp math concepts better and make your lessons more effective and engaging, no matter where your students are starting from.
1. Use Formative Assessment to Guide Instruction
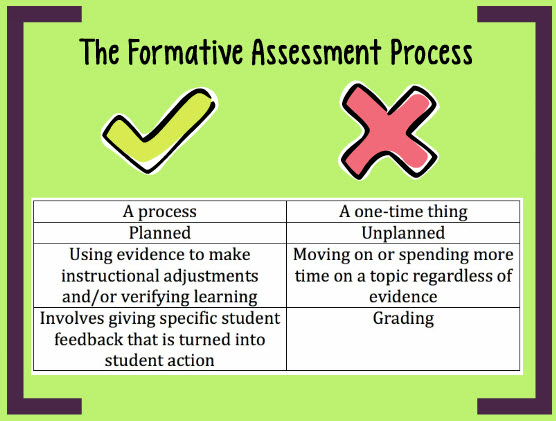
Formative assessment is an ongoing process where you check students’ understanding during the lesson, which is especially helpful when teaching elementary math. It helps you see if they’re following along or getting stuck, so you can adjust your teaching in real-time.
Why it works: Math concepts build on each other, so if students don’t grasp the basics, they’ll struggle with more complex ideas later. Formative assessments let you catch misconceptions early, helping prevent future confusion.
How do I implement this?
- Quick Quizzes or Exit Tickets: At the end of a lesson, use a short quiz, worksheet, or exit ticket with 2-3 key questions to see if students understood the day’s content. Worksheets can serve as structured exit tickets, offering a quick way to assess understanding and identify any areas that may need review in the next lesson. Here are over 6,000 math teaching practice worksheets to get you started:
Begin here
- Thumbs Up/Down: During class, ask students to signal with a thumbs up if they understand, or a thumbs down if they’re confused. This gives you a quick snapshot of where they stand.
- Mini-Whiteboards: Give each student a mini-whiteboard. Ask a problem, and have them write their answer and hold it up. This way, you can instantly see who’s getting it and who’s not.
- Grouping Students: Based on their responses, group students for targeted support. Those who understand can move to enrichment activities, while others can work on foundational skills with you.
2. Employ Explicit Instruction for Key Concepts
Explicit instruction involves teaching math concepts step-by-step, where the teacher models the process, guides students through examples, and gradually hands over responsibility for independent practice.
Why it works: Math can be overwhelming when students are given too much information at once. Explicit instruction breaks down complex skills into smaller, manageable steps. This helps students build a solid foundation and prevents them from feeling lost during lessons.
How do I implement this?
- Prepare in Advance: Effective explicit instruction requires thorough lesson planning. Before class, plan each step of the lesson, including objectives, examples, and possible student difficulties. This preparation allows you to stay organized and ensure a logical flow, so students can follow along without confusion. Without a clear plan, it becomes challenging to deliver structured instruction and provide the necessary guidance.
The best way to teach math, save time and ensure you’re fully prepared, is using these free expert-created, ready-to-use lesson plans. These plans are designed by experienced teachers and are structured to support explicit instruction. They help you stay organized, provide step-by-step guidance, and ensure that key concepts are covered comprehensively. This way, you can focus more on delivering engaging lessons without worrying about planning from scratch.
Begin here
- Step-by-Step Modeling: Begin by clearly explaining the objective of the lesson. For example, if you’re teaching long division, start by walking through the process on the board, talking through each step aloud. Show them exactly how to approach the problem.
- Think-Alouds: As you work through a problem, verbalize your thinking. Say things like, “First, I divide… then I bring down…” This gives students a clear sense of the logic and decision-making behind each step.
- Guided Practice: After modeling, have students try similar problems with your support. You can solve a problem together as a class or in small groups. For example, you might solve the first part of the equation and ask them to complete the next steps.
3. Gamify Math Concepts to Boost Engagement

Gamification involves turning math lessons into games or incorporating game-like elements, such as points, levels, or rewards, to make learning math more interactive and engaging for students.
Why it works: Gamifying math taps into students’ natural love for play and competition, making learning more fun. It boosts motivation, keeps students engaged, and can even reduce math anxiety. Games provide immediate feedback, helping students quickly understand if they’re on the right track.
How do I implement this?
- Use Online Math Games:
Begin here
- SplashLearn offers a wide variety of games that break math concepts into manageable chunks. These games allow students to practice at their own pace. The engaging, colorful environment of the games takes the pressure off, encouraging students to focus on solving problems rather than worrying about getting things wrong.
- Reduces Math Anxiety Through Positive Reinforcement: One key way SplashLearn reduces math anxiety is by using positive reinforcement. In games, mistakes aren’t penalized—instead, students get encouraging feedback like “Let’s try again!” This helps students view errors as learning opportunities rather than failures, shifting their mindset to one of growth rather than perfection. The removal of traditional grading helps alleviate the pressure, allowing students to take on challenges without fear.
- Personalized Learning to Lower Stress: The games in SplashLearn are designed to adapt to each student’s level. If a student is struggling, the game automatically adjusts, offering simpler problems or additional practice in a supportive way. This prevents students from feeling overwhelmed by material that’s too difficult, keeping the experience enjoyable while helping them improve step by step.
- Game Progress and Rewards for Confidence Building: As students advance in the games, they earn rewards, badges, and unlock new levels. This progress builds confidence and provides a sense of accomplishment without the anxiety of traditional assessments.
- Math Board Games or Card Games: Create custom math board games with dice and flashcards. For example, students might roll dice to generate numbers and then use them to create equations that fit specific criteria, such as “make the largest product.”
- Leveling Up: Introduce a “level-up” system in class, where students earn points or badges for completing math tasks, mastering concepts, or helping their peers. For instance, a student might earn a badge for mastering fractions or for consistently improving their quiz scores.
- Math Escape Rooms: Create a math “escape room” where students must solve a series of math problems to unlock clues and “escape” within a certain time limit. For example, solving each problem could reveal the next clue, such as a combination to a lock or the next math challenge.
Related Reading: Best Game-Based Learning Platforms for Kids
4. Mathematical Discourse with Structured Talk Moves
Mathematical discourse involves encouraging students to talk about their thinking and explain how they solve problems, which is a key strategy when considering how to teach math effectively. Structured “talk moves” guide these discussions, helping students clarify and deepen their understanding through conversation.
Why it works: When students explain their reasoning, they process math at a deeper level. Engaging in math conversations also helps clear up misconceptions, as students articulate their thoughts and listen to others’ perspectives.
How do I implement this?
- Revoicing: When a student gives an answer, restate it in your own words and ask if you’ve understood correctly. For example, “So, you’re saying you multiplied by 4 because you saw a pattern?” This gives the student a chance to clarify their thinking.
- Ask for Elaboration: Encourage students to expand on their answers by prompting them with questions like, “Can you explain why you chose that method?” or “How did you know to divide here?”
- Peer Explanation: Have students explain another classmate’s thinking. For instance, “Can someone repeat what Jenna just said, but in your own words?” This reinforces listening skills and encourages deeper understanding.
- Multiple Strategies Discussion: After solving a problem, ask students if anyone solved it in a different way. For example, after finding the answer to a multiplication problem, ask, “Did anyone use a different strategy, like breaking the numbers apart?”
5. Apply Spaced Repetition and Interleaved Practice
Spaced repetition involves revisiting math concepts over time to reinforce learning. Interleaved practice mixes different types of problems in a single session, instead of focusing on just one skill at a time.
Why it works: Students often forget math concepts if they aren’t reviewed regularly. Spaced repetition helps move information into long-term memory by revisiting material at intervals. Interleaving different types of problems in one session improves problem-solving flexibility, as students learn to apply various strategies in different contexts.
How do I implement this?
- Spaced Repetition: Instead of teaching a topic once and moving on, bring it back in future lessons. For example, if you taught fractions two weeks ago, include a few fraction problems in today’s warm-up. Repeat this every few weeks to keep concepts fresh.
- Interleaved Practice: During practice sessions or homework, mix problems from different units. For example, instead of a worksheet only on multiplication, include problems on division, fractions, and geometry. This helps students see connections between concepts and strengthens their ability to switch between different strategies.
- Cumulative Reviews: Include a small section of review questions from past units in each quiz or test. For instance, if you’re covering decimals, add a few questions on place value or basic arithmetic from earlier in the year.
6. Engage Students in Error Analysis to Build Conceptual Understanding
Error analysis involves having students examine and correct mistakes in math problems. This approach helps them understand not only the right answer but also why errors happen and how to avoid them.
Why it works: When students analyze mistakes, they gain insight into common misconceptions and deepen their understanding of the math process. It also encourages critical thinking, as students must reflect on why something went wrong and how to fix it.
How do I implement this?
- Intentional Mistakes: Present students with problems that contain common errors, like incorrect order of operations or a misstep in factoring. Ask them to find the mistake, explain why it’s wrong, and correct it. For example, show a miscalculated long division problem and ask them to identify where the process broke down.
- Peer Review: Have students swap their work and check each other’s answers. Encourage them to find and explain any mistakes, rather than just marking them wrong. This helps students learn from one another and reinforces understanding.
- Class Discussions: Work through a problem that includes a mistake together as a class. Ask guiding questions like, “What did the student do wrong here? What should have been done instead?” This promotes collaborative problem-solving and exposes students to different thinking processes.
- Reflection Journals: After students correct their errors, ask them to write about why the mistake happened and how they can avoid it in the future. For example, they could write, “I forgot to distribute the negative sign, so next time I’ll double-check my signs.”
7. Use Manipulatives to Bridge Concrete and Abstract Thinking
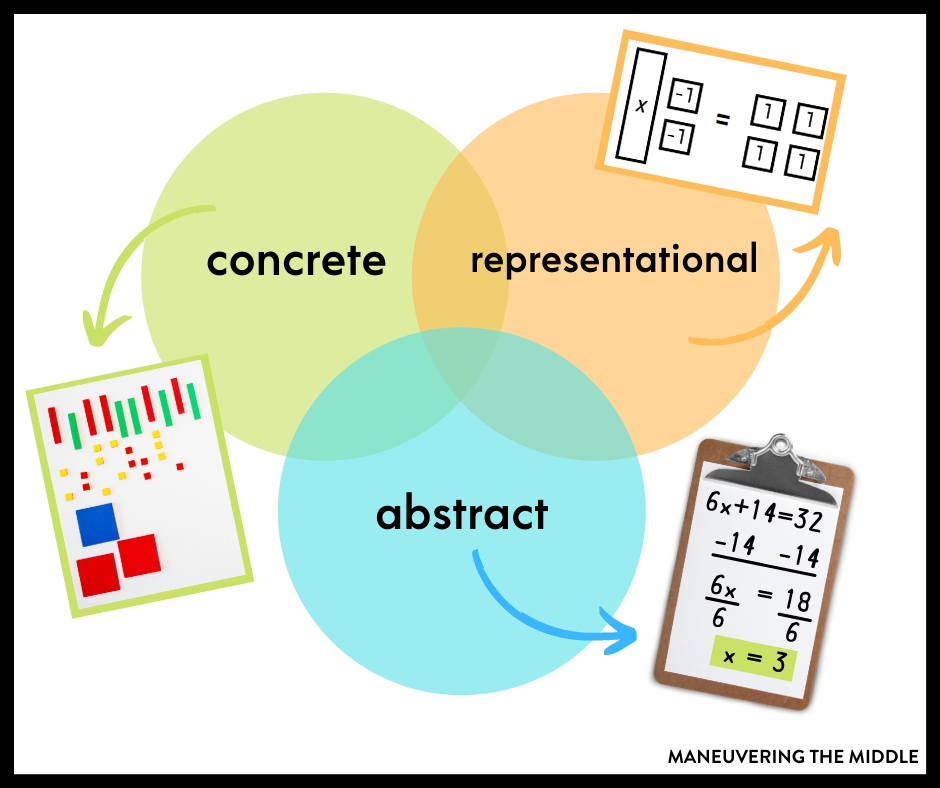
Manipulatives are physical tools, like base-10 blocks or fraction tiles, that help students visualize and understand abstract math concepts. They serve as a bridge between hands-on learning and more abstract thinking, like using symbols or equations.
Why it works: Many students struggle to grasp abstract math concepts when taught with just numbers or symbols. Manipulatives provide a concrete way to see and physically interact with math, making it easier for students to understand the underlying concepts before moving to abstract representations.
How do I implement this?
- Digital Resources: Interactive digital tools and virtual manipulatives feature engaging, educational elements that make learning math more intuitive and fun for students.
Here are some free resources that go beyond traditional methods by offering visual and hands-on learning experiences through user-friendly interfaces. They align perfectly with modern math instructional strategies, helping students explore and manipulate abstract concepts like fractions or number lines in a concrete and more interactive way. This approach builds stronger conceptual understanding.
Begin here
- Introduce New Concepts: When teaching something new, like place value or fractions, start with manipulatives. For example, use base-10 blocks to show how numbers are built or fraction bars to demonstrate adding fractions with different denominators.
- Transition Gradually: Once students are comfortable with the concept, slowly phase out the manipulatives and introduce more abstract tools like equations or diagrams. For instance, after students understand fractions using bars, move to solving fraction problems using numbers and symbols.
- Group Work: Let students use manipulatives in pairs or small groups to solve problems. For example, if you’re teaching algebra, you could use algebra tiles to visually represent equations, then have students balance and solve them together.
- Support Struggling Students: Manipulatives are especially helpful for students who need more support. If a student is struggling with subtraction, give them counters or number lines to help them visualize the process before asking them to solve it with numbers alone.
8. Apply the Gradual Release of Responsibility Model (I Do, We Do, You Do)
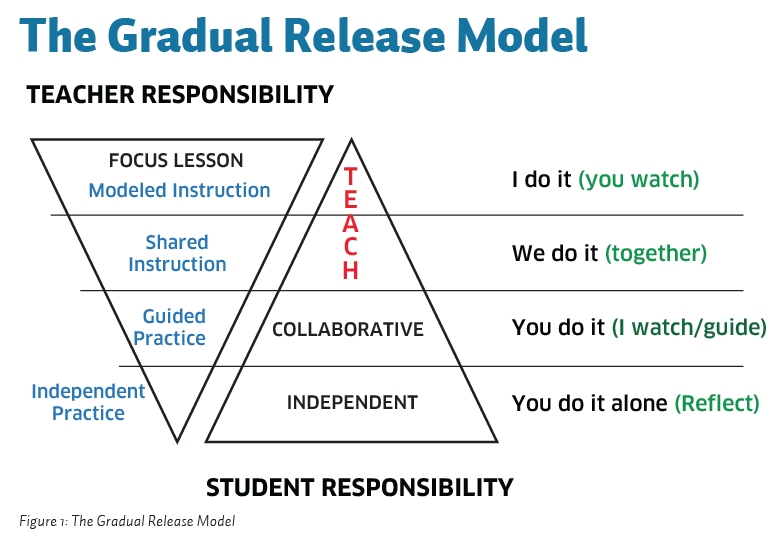
The Gradual Release of Responsibility (GRR) model involves shifting the learning process from teacher-led instruction to student independence through three stages: “I Do” (teacher models), “We Do” (guided practice), and “You Do” (independent work).
Why it works: This method ensures that students get the right amount of support when learning new concepts. Starting with teacher modeling builds confidence, and gradually reducing support helps students develop the skills to solve problems on their own.
How do I implement this?
- I Do (Teacher Models): Begin by clearly demonstrating the math concept or skill while thinking aloud. For example, if teaching how to solve an equation, work through each step slowly, explaining your reasoning at every point. Say things like, “First, I’m going to isolate the variable by subtracting 5 from both sides.”
- We Do (Guided Practice): Next, work through a few problems together with the class. Call on students to help solve the problem while guiding them through each step. For instance, ask, “What’s the next step after isolating the variable?” and provide support as needed. This collaborative phase allows students to practice with your help, reinforcing understanding.
- You Do (Independent Practice): Once students show they understand, let them solve problems independently. Circulate the room to provide help where needed but encourage students to try solving on their own first. For example, after practicing a few problems as a class, assign similar problems for students to tackle solo, and offer quick feedback.
- Check for Understanding: After the independent work, review common mistakes or misconceptions with the class. This is a great time to address any confusion and ensure students are confident moving forward.
9. Teach Problem-Solving with Polya’s Four-Step Process
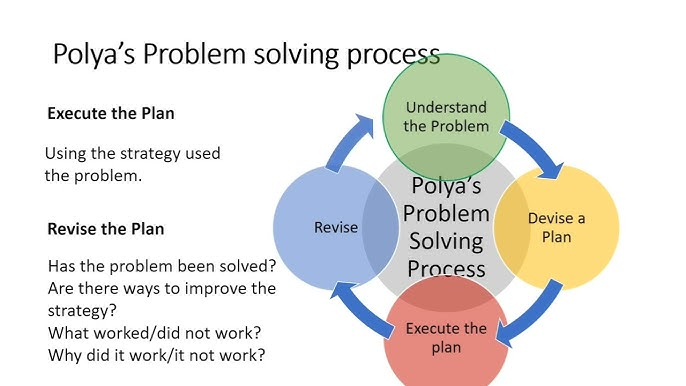
Polya’s Four-Step Process is a structured math teaching method for solving problems, which includes: 1) Understand the problem, 2) Devise a plan, 3) Carry out the plan, and 4) Review the solution.
Why it works: This step-by-step approach helps students tackle problems methodically. Instead of jumping straight into solving, it encourages students to think critically about what the problem is asking and how to approach it.
How do I implement this?
- Step 1: Understand the Problem: Teach students to start by reading the problem carefully. Encourage them to restate the problem in their own words or identify the key information. For example, in a word problem about distance and time, ask them, “What is the question asking us to find?”
- Step 2: Devise a Plan: Once they understand the problem, help students create a strategy. This might involve choosing the right formula, drawing a diagram, or breaking the problem into smaller steps. For instance, if they’re solving an area problem, their plan might involve identifying the shape and applying the area formula.
- Step 3: Carry Out the Plan: Have students implement their chosen strategy step by step. This is where they apply the math concepts they’ve learned. Remind them to work through the problem carefully and check their steps as they go along.
- Step 4: Review the Solution: After solving, encourage students to review their solution to see if it makes sense. Ask questions like, “Does the answer fit the context of the problem?” or “Did I follow all the steps correctly?” This reflection helps students catch mistakes and solidifies their understanding.
- Example: For a problem involving finding the perimeter of a rectangle, students would: 1) Identify the length and width, 2) Devise a plan to add the sides together, 3) Carry out the addition, and 4) Check to make sure the answer matches the dimensions.
10. Use Visual Representations to Enhance Comprehension
Visual representations, such as diagrams, graphs, and models, help students understand abstract math concepts by providing concrete visuals that make the ideas easier to grasp.
Why it works: Many students are visual learners, and abstract math concepts like fractions, geometry, or algebra can be hard to understand without a visual aid. Using visual tools makes math more accessible, helping students see the relationships between numbers and operations.
How do I implement this?
- Bar Models: For word problems, use bar models (also called tape diagrams) to break down the parts of the problem visually. For example, when teaching ratios, students can draw bars to represent different parts and see how they relate to each other.
- Number Lines: Use number lines to teach topics like addition, subtraction, fractions, and decimals. For example, when teaching negative numbers, students can visually see how numbers decrease as they move left on the number line.
- Graphs: For algebraic equations, show students how to plot the equation on a graph. This can help them understand the concept of slope and intercepts in a linear equation. For instance, have them graph y = 2x + 3 and see how the line represents solutions to the equation.
- Geometry Tools: Use visual aids like protractors, rulers, and grid paper when teaching geometry. For example, when teaching area or perimeter, students can draw shapes to better understand the formula application.
- Fraction Circles or Bars: When teaching fractions, use visual tools like fraction circles or bars. This helps students physically see how fractions compare or combine. For instance, show how 1/4 and 2/4 add up by combining fraction bars.
Related Reading: How to Make Math Fun for Kids
Conclusion
Understanding how to teach math effectively involves breaking down concepts, engaging students, and constantly assessing their progress. By incorporating effective math teaching strategies like explicit instruction, formative assessments, and spaced repetition, teachers can help students build a strong foundation and reduce confusion. Remember, adjusting your approach based on student needs will make lessons more impactful and ensure lasting comprehension.
Related Reading: Best Math Tricks for Kids to Make Learning Super Fun
Frequently Asked Questions (FAQs)
What are some of the best strategies for teaching math for beginners?
Some of the best strategies for teaching math to beginners include explicit instruction, which breaks down concepts into simple steps, and using visual aids like number lines or manipulatives to help students understand abstract ideas. Formative assessments can also ensure students grasp the basics before moving on to more complex concepts.
What are the best approaches to teach math?
When considering approaches to teach math, you can use strategies like gamification to make learning fun, spaced repetition to reinforce learning over time, and error analysis to help students learn from mistakes. These approaches cater to different learning styles and help students build a strong foundation in math.
What is the easiest way to teach a child math?
The easiest way to teach a child math is to use hands-on activities and visual tools that make abstract concepts concrete. Incorporating games, puzzles, and real-world examples keeps them engaged. To understand how to teach math effectively, focus on breaking down problems into simple, manageable steps and ensuring frequent practice.