60 Degrees to Radians – Definition, Formula, Examples, Facts, FAQs

What Is 60 Degrees to Radians Conversion?

60 degrees to radians is $\pi 3$. 

Degrees and radians are the units used to measure angles. 

Degree: A degree (denoted by °) is the amount of rotation from the initial arm to the terminal arm. A complete turn around the center of a circle is $360^{\circ}$. If it is divided into 360 equal parts, each part represents 1 degree.

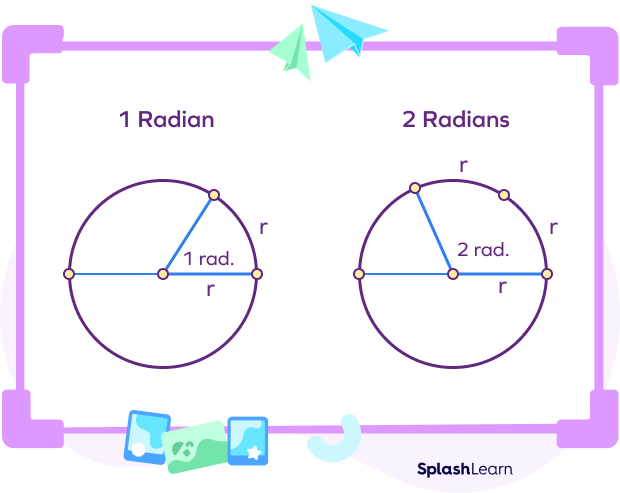
Radian: An angle of 1 radian is defined to be the angle, in the counterclockwise direction, which spans an arc whose length is equal to the radius of the circle. Thus, if arc length $= r$, then angle is 1 radian. It holds true for all circles.  

By the same logic, 2 radians is the central angle made by an arc whose length is $2 r$ (twice the length of the radius of the circle). If the arc-length equals the total circumference of the circle which is $2\pi r$, it represents an angle of $2\pi$ radians. Thus, a complete circle represents $2\pi$ radians. 

• $360^{\circ} = 2\pi$ radians
• $180^{\circ} = \pi$ radians
• $90^{\circ} = 2$ radians
• $60^{\circ} = 3$ radians
• $45^{\circ} = 4$ radians   
• $30^{\circ} = 6$ radians 

Degrees to Radians Formula

To convert an angle from degrees to radians, we multiply it by $180^{\circ}$.

We can use this formula to convert 60 degrees to radians.

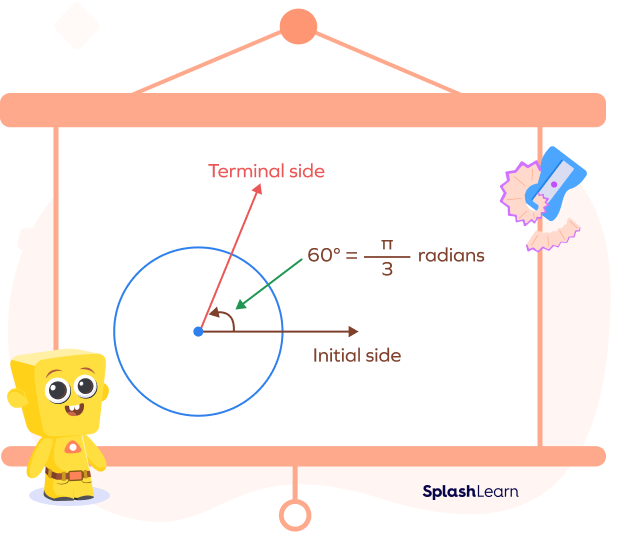
How to Convert 60 Degrees into Radians

We use the conversion formula to convert 60 degrees into radians.

Angle in radians $=$ Angle in degrees $\times\frac{\pi}{180^{\circ}}$

Here, angle in degrees $= 60^{\circ}$

On substituting this in the formula, we get

Angle in radians $= 60^{\circ} \times \frac{\pi}{180^{\circ}} = \frac{\pi}{3}$

Thus, the value of 60 degrees to radians is 3.

Note:

We can also approach this problem in a different way. We know that the angle at the center of a circle is 360 degrees. It is equivalent to 2π in radians. 

$360^{\circ} = 2\pi$

Dividing both sides by 6, we will get 

$\frac{360^{\circ}}{6} = \frac{2\pi}{6}$

$60^{\circ} = \frac{\pi}{3}$ 

Thus, the value of 60 degrees to radians in terms of pi is $\frac{\pi}{3}$.

Negative 60 Degrees to Radians

Negative angle is an angle generated in an clockwise direction from the initial arm. To convert a negative degree into a radian, we use the same method as we did for positive degrees. We will simply multiply the angle’s given value by $\frac{\pi}{180^{\circ}}$.

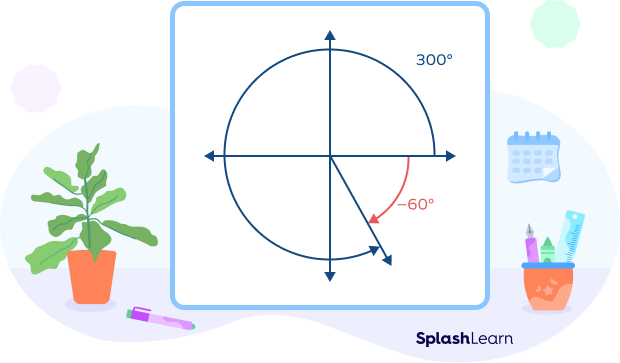
Let’s convert $-60^{\circ}$ into radians.

Radian $= (\frac{\pi}{180^{\circ}})$   (degrees)

Radian $= (\frac{\pi}{180^{\circ}}) \times (-60^{\circ})$

Angle in radian $= – \frac{\pi}{3}$

Facts about 60 Degrees to Radians

Conclusion

In this article, we learned about the angle in radians equivalent to 60 degrees. We discussed the conversion formula along with some examples. Let’s solve a few more examples and practice problems for better understanding.

Solved Examples on Degrees to Radians

1. Convert 60 degrees to radians.

Solution: 

To convert $60^{\circ}$ to radians, use the formula

Angle in radians $=$ Angle in degrees $\times (\frac{\pi}{180^{\circ}})$

Therefore, $60^{\circ} \times (\frac{\pi}{180^{\circ}}) = (\frac{\pi}{3})$  radians 

So, 60 degrees in radians is $(\frac{\pi}{3})$  radians.

2. Convert 90 degrees to radians.

Solution: 

Given: 90 degrees is the angle

Angle in radian $=$ Angle in degree $\times (\frac{\pi}{180^{\circ}})$

Angle in radian $= 90^{\circ} \times (\frac{\pi}{180^{\circ}})$

Angle in radian $= \frac{\pi}{2}$

Hence, 90 degrees is equal to $\frac{\pi}{2}$ in radians.

3. Convert 49 radians to degrees. 

Solution: 

Angle in Degrees $=$ Angle in Radians $\times \frac{\pi}{180^{\circ}}$

Angle in Degrees $= (\frac{4\pi}{9}) \times \frac{\pi}{180^{\circ}}$

Angle in Degrees $= 4 \times 20^{\circ}$

Angle in Degrees $= 80^{\circ}$

Hence, $\frac{4\pi}{9}$  radians are 80 degrees. 

4. Convert 200 degrees into radians.

Solution: 

By the formula, we know

Angle in radians $=$ Angle in degree $\times \frac{\pi}{180^{\circ}}$

Thus, 200 degrees in radians  $= 200 \times \frac{\pi}{180^{\circ}} = \frac{10\pi}{9}$ radians.

Hence, 200 degrees is equal to $\frac{10\pi}{9}$ in radians.

Practice Problems on Degrees to Radians

Frequently Asked Questions about Degrees to Radians