Definition of Decimal Fractions
The prerequisite for understanding decimal fractions is the understanding of normal fractions. You must know that a fraction comprises a numerator (top part) and a denominator (bottom part). The correct way of writing a fraction is –
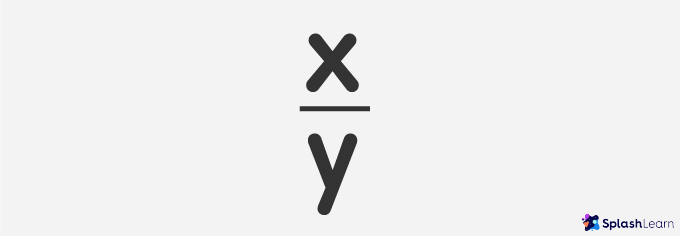
X is the numerator in this example, and y is the denominator.
Decimal fractions are the fractions in which the denominator (y in the image) must be 10 or a multiple of 10 like 100, 1000, 10000, and so on. The numerator can be any integer (between -infinity and +infinity). These decimal fractions are usually expressed in decimal numbers (numbers with a decimal point).
In algebra, a decimal fraction is a number having 10 or the powers of 10 like 10¹, 10², 10³, and so on in the denominator.
Recommended Games
Examples of Decimal Fractions
- 7/10000 is a decimal fraction written in the decimal form as 0.0007.
- 19/10 is a decimal fraction written in the decimal form as 1.9.
- 39/1000 is a decimal fraction written as 0.039.
Non Examples of Decimal Fractions
Other fractions with non-ten numbers in the denominator are not decimal fractions. They are:
- 37/8
- 2/1083
- 83/145
Reading Decimal Fractions
Let us consider a scenario where 1 is in the numerator. We will consider different denominators to understand how these terms are read with this numerator.
- 1/10 is read as one-tenth.
- 1/100 is read as one-hundredth.
- 1/1000 is read as one-thousandth.
When the value of the numerator is more than one, we add an ‘s’ to the name. So, for instance, 3/10 is read as three-tenths.
History of Decimal Fractions
The Chinese first developed and used decimal fractions at the end of the 4th century BC, which spread to the Middle East before reaching Europe.
Conversion to Decimal Fractions
1. Conversion from fractions to decimal fractions:
- Let us consider an example of a fraction, 3/2.
- The first step would be to consider the number that gives 10 or a multiple of 10 when multiplied by the denominator. In this case, 5 multiplied by 2 gives 10.
- Now multiply the numerator and denominator with the same number to get your decimal fraction. Here, 3 x 5/ 2 x 5 gives 15/10.
- Thus, the decimal fraction of 3/2 is 15/10.
2. Conversion from mixed numbers to decimal fractions:
- Convert the mixed fraction into a normal fraction.
- Follow the steps for converting fractions to decimal fractions.
3. Conversion from decimal numbers to decimal fractions:
- Write the original decimal number in the numerator and denominator form by placing 1 in the denominator: 4.3/1.
- For every space that you move the decimal point, add a zero next to the 1 in the denominator: 43/10 (As we can see one shift of decimal space, one 0 must be added to the denominator).
4.3/1
43.0/10
- Once the number in the numerator is non-decimal, you have got your decimal fraction: 4.3 = 43/10.
Real-Life Application of Decimal Fractions
Decimal fractions are used for understanding precise quantities instead of whole numbers. You will also use them for expressing percentages. For instance, 97% can be written as 97/100 for ease of calculation.
Here are some scenarios where you might encounter decimal fractions:
- Coins (They are a fraction of Rupees)
- Weighing products
- Measuring ingredients while cooking
Recommended Worksheets
Solved Examples on Decimal Fraction
Example 1
Convert 2 ½ into a decimal fraction.
= 2 ½
= 5/2
= 5 x 5 / 2 x 5
= 25 / 10
Example 2
Convert 5.4 into a decimal fraction.
= 5.4/1
= 54/10
Example 3
Convert 8 ⅕ into a decimal fraction.
= 8 ⅕
= 41/5
= 41 x 2 / 5 x 2
= 82/10
Conclusion
Decimal fractions encourage students to learn about precise quantities. This will help them understand weights like 3.2 kg and distances like 7.85 km. The first step towards a better understanding of decimal numbers is practicing decimal fraction problems every day. The idea of taking a pen and paper to solve sums is dull and uninteresting for students. They need entertaining ways to entice them towards practicing the sums.
SplashLearn makes the process of practicing decimal numbers fun and interactive for kids. With dozens of decimal fraction games, your child will never fall short of options to practice math. Instead, learning becomes engaging with interesting games that allure your kids towards solving sums.
Let’s do it!
Instead of teaching decimal fractions and handing out practice worksheets to your children, ask them to find and make decimal fractions of the decimals or fractions you say.
Practice Problems on Decimal Fraction
Decimal Fraction
Convert 6.34 into a decimal fraction.
Since there are two places after the decimal point, the decimal fraction of 6.34 would be 634/100.
Convert 4 ½ into a decimal fraction.
4 ½ can be written as 4.5 and since there is only one place after the decimal point, it’s decimal fraction would be 45/10.
Convert 8/5 into a decimal fraction.
Multiplying the numerator and the denominator by 2 we get, 8/5 = 16/10
Convert 5/4 into a decimal fraction.
Multiplying the numerator and the denominator by 25 we get, 5/4 = 125/100
Frequently Asked Questions on Decimal Fraction
What is a decimal fraction example?
A decimal fraction is a fraction with a power of 10 (10^1, 10^2, etc.) in the denominator. These numbers are written in decimal form for the convenience of solving mathematical sums. For example, 4/1000 is a decimal fraction, written in decimals as 0.004.
How do you write a decimal fraction?
A decimal fraction is written as any number in the numerator with 10 and multiples of 10 in the denominator.
What is a decimal fraction in the simplest form?
The simplest form of a decimal fraction is the basic in-divisible fraction obtained by dividing the numerator by the denominator. For example, the simplest form of the decimal fraction 4/10 is 2/5.
Can all percentages be expressed as decimal fractions? Give an example.
Yes. All percentages can be expressed as decimal fractions. For instance, 80% is written as 80/100 in the decimal fraction form. This can be further divided to get the simplest form 4/5 of the decimal form.
Where are decimal fractions used?
Decimal fractions are used for expressing the weight of people and products. It can also be used to determine discounts on the price of products and measure the ingredients of a recipe.




































