Volume of a Prism – Introduction
The definition of the volume of a prism can be simply given as the space occupied by the prism. A prism is a three-dimensional figure that has flat sides and two identical bases.
The bases of a prism are polygons, like a triangle, a square, a rectangle, or a hexagram. Prisms are often named after the polygons that form the base.
To find the volume, we need to know the prism’s base area and height.
Recommended Games
What Is the Volume of a Prism?
The volume of a prism can be defined as the space it occupies in cubic units. Cubic units measure the volume of a three-dimensional figure.
To find the volume, we multiply the base area with the height of the prism.
The base area is the surface area of the base. The height is the column connecting the two bases of the prism.
When we multiply the base with the height, the resulting volume will be measured in cubic units such as cubic inches, cubic yards, cubic feet, cubic centimeters, or cubic meters.
To find the volume, the base area and height are the only values we need to know.
What Is the Formula for the Volume of a Prism?
The volume of a prism formula is:
Volume $=$ base area $\times$ height
We can find the volume of any prism using this formula.
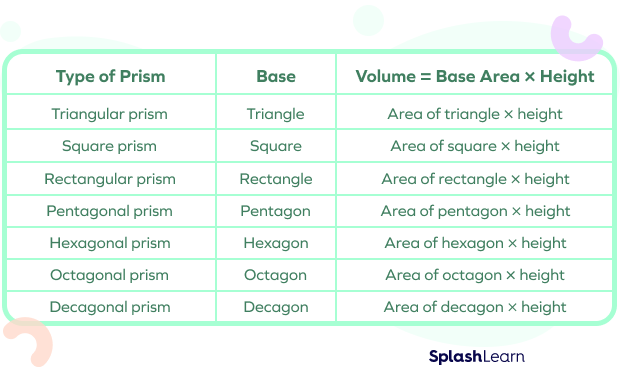
Formulas for different prisms are discussed in the following table.
Table of Formulas for Different Types of Prisms
How to Find the volume of a prism?
The formula to calculate the prism volume can be written as $\text{V} = b \times h$, where V is the volume, b is the base area, and h is the height of the prism.
Finding volume of a prism example:
Let us find the volume of a prism whose base area is 5 square inches and height is 10 inches.
Applying the formula:
$\text{V} = b \times h$
Volume $= 5 \times 10 = 50$ cubic inches.
Fun Facts!
- We can apply the volume of a prism equation to find the volume of different types of prisms.
- The volume depends on the shape of its base since that will determine the base area.
- The base area of a prism is measured in square units, square inches, or square meters since it represents a two-dimensional area, i.e., the surface area of the prism base.
- The height of a prism is measured in regular units like inches or meters. This is because it represents the length of the column that connects the bases.
Conclusion
Finding the volume of a prism is easy once you get the hang of the formula. Remember, it doesn’t matter what type of prism it is. As long as you know the height and the base area, you can find its volume!
Solved Examples
1. What is the base area of a prism if the volume of the prism is 150 cubic feet and the height of the prism is 10 feet?
Solution: Applying the formula:
$\text{V} = b \times h$
$150 = b \times 10$
$b = 150 / 10 = 15$ square feet
2. The base of a prism has a surface area of 277 square centimeters. The volume is 2770 cubic centimeters. Calculate the height.
Solution: Applying the formula:
$\text{V} = b \times h$
$2770 = 277 \times h$
$h = 2770 / 277 = 10$ centimeters
3. The height of a square prism is 11 yards. The volume is 99 cubic yards. What is the length of the side of the square at the base of the prism?
Solution: Volume = base area x height
Applying the formula:
$\text{V} = b \times h$
$99 = b \times 11$
$b = \frac{99}{11} = 9$ square yards
Since the base area is 9 square yards, this is the area of the square base of the prism. So, the side of the square will be the square root of $9 = 3$ yards.
4. The base of a prism has a surface area of 475 square centimeters. The volume is 3800 cubic centimeters. Calculate the height.
Solution: Applying the formula:
$\text{V} = b \times h$
$3800 = 475 \times h$
$h = \frac{3800}{475} = 8$ centimeters
5. The column of a prism has a length of 20 meters. The base of the prism has an area of 25 square meters. What is the volume of the prism?
Solution: Applying the formula:
$\text{V} = b \times h$
$\text{V} = 25 \times 20 = 500$ cubic meters
Practice Problems
Volume of a Prism - Definition With Examples
What is the base area of a prism if the volume of the prism is 300 cubic feet and the height of the prism is 6 feet?
$\text{V} = b \times h$
$300 = b \times 6$
$b = \frac{300}{6} = 50$ square feet
The base of a prism has a surface area of 25 square centimeters. Its volume is 125 cubic centimeters. Calculate the height.
$\text{V} = b \times h$
$125 = 25 \times h$
$h = \frac{125}{25} = 5$ centimeters
The base area of a prism is 123 square yards. The height is 9 yards. Find the volume.
Applying the formula, $\text{V} = b \times h$
$\text{V} = 123 \times 9$
$= 1107$ cubic yards
The base of a prism has a surface area of 12 square centimeters. The volume of the prism is 144 cubic centimeters. Calculate the height.
$\text{V} = b \times h$
$144 = 12 \times h$
$h = \frac{144}{12} = 12$ centimeters
The column of a prism has a length of 100 feet. The base of the prism has an area of 25 square feet. What is its volume?
$\text{V} = b \times h$
$\text{V} = 25 \times 100 = 2500$ cubic feet
Frequently Asked Questions
Irregular prisms have irregular polygons as their bases. This means the base shapes have different angles, and the sides are not equal in length. Though the base area will differ, the formula for finding volume will be the same, i.e., base area $\times$ height.
Is the volume of a prism affected by the number of faces it has?
No, the volume of a prism is not affected by the number of faces because its base area and height are not changed by the number of faces.
How does the volume differ between different types of prisms?
Different types of prisms have different bases of different shapes and sizes. Since the base area differs, the volume will differ accordingly.
How is volume related to the side of the base polygon in a regular prism?
The longer the side of the base polygon, the greater the base area and, therefore, the more the volume.
How do you calculate the volume of a right prism?
A right prism is a prism in which the angles between the base and the sides (lateral faces) of the prism are right angles, for example, a rectangular prism. The formula to find the volume is the same: V $= b \times h$.

























