What is a Polygon?
In geometry, a polygon can be defined as a flat or plane, two-dimensional closed shape bounded with straight sides. It does not have curved sides. The sides of a polygon are also called its edges. The points where two sides meet are the vertices (or corners) of a polygon.
Here are a few examples of polygons.
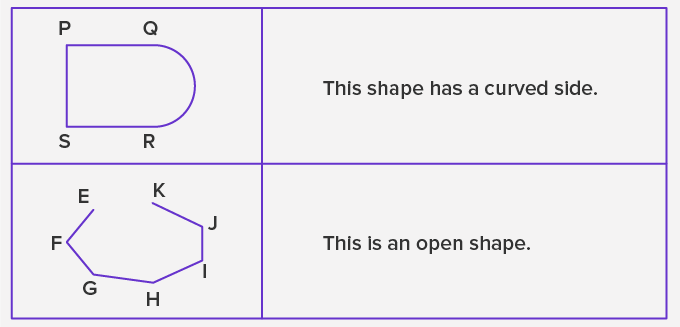
Here are a few non-examples of a polygon
Recommended Games
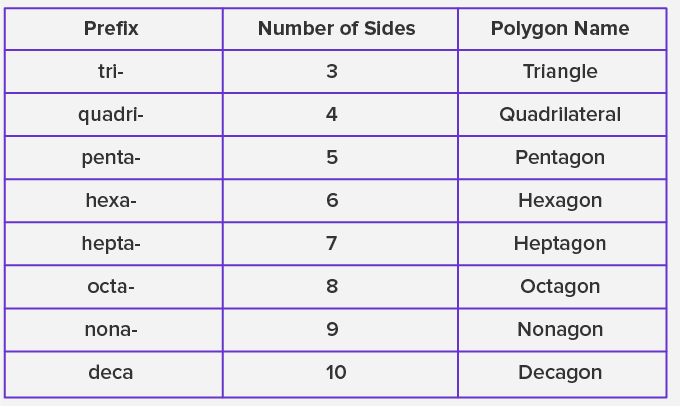
Polygon Chart
Polygons are named on the basis of the number of sides it has. Polygons are generally denoted by n-gon where n represents the number of sides it has, For example, a five-sided polygon is named as 5-gon, a ten-sided is named as 10-gon, and so on.
However, few polygons have some special names. The minimum number of sides a polygon can have is 3 because it needs a minimum of 3 sides to be a closed shape or else it will be open.
Even though polygons with sides greater than 10, also have special names, we generally denote them with n-gon as the names are complex and not easy to remember.
Types of Polygon
The polygons can be classified on the basis of the number of sides and angles it has:
- Classification on the basis of sides: Regular and Irregular Polygons:
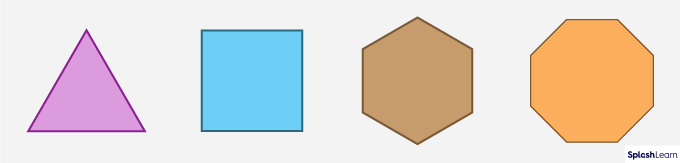
Regular Polygons – Polygons that have equal sides and angles are regular polygons.
For example, an equilateral triangle is a three-sided regular polygon. A square is a four-sided regular polygon. A Regular hexagon is a six-sided regular polygon.
Here are a few examples of regular polygons.
Irregular Polygons – Polygons with unequal sides and angles are irregular polygons.
Here are a few examples of irregular polygons.
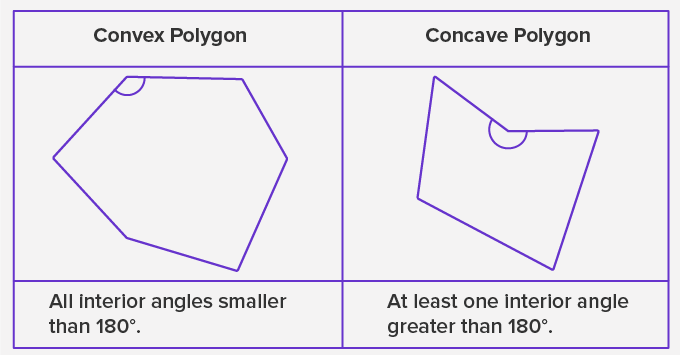
- Classification on the basis of angles: Convex and Concave Polygons:
Convex Polygons – A convex polygon is a polygon with all interior angles less than 180°.
In convex polygons, all diagonals are in the interior of the polygon.
(Diagonal is a line segment joining any two non-consecutive vertices of a polygon)
Here are a few examples of convex polygons.

Concave Polygons – A concave polygon is a polygon with at least one interior angle greater than 180°.
In concave polygons, not all diagonals are in the interior of the polygon.
Here are a few examples of concave polygons.
Difference between Convex and Concave Polygon
3. Simple and Complex Polygon:
Simple Polygon – A simple polygon has only one boundary. The sides of a simple polygon do not intersect.

Complex Polygon – Complex polygon is a polygon whose sides cross over each other one or more times.

Sum of Angles of a Polygon
1. Sum of the interior angles of a polygon:
Sum of the interior angles of a polygon with n sides = (n – 2) × 180°
For example: Consider the following polygon with 6 sides
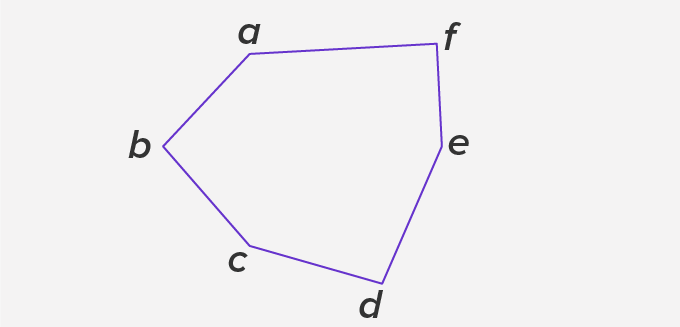
Here, ∠a + ∠b + ∠c + ∠d + ∠e + ∠f = (6 – 2) × 180° = 720° (n = 6 as given polygon has 6 sides)
2. Sum of the exterior angles of polygons
Sum of the exterior angles of polygons = 360°
The sum will always be equal to 360 degrees, irrespective of the number of sides it has.
For example: Consider the following polygon with 5 sides
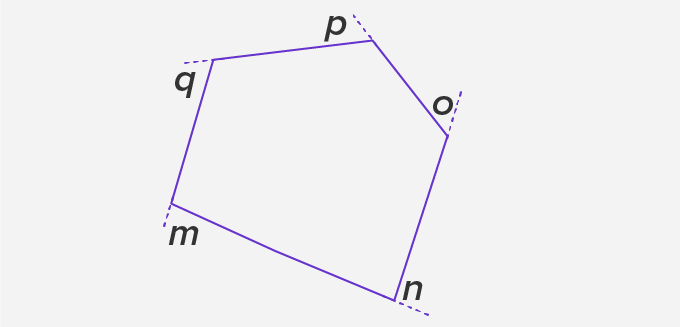
Here, ∠m + ∠n + ∠o + ∠p + ∠q = 360°
Angles in Regular Polygon
In a regular polygon, all its
- sides are equal
- interior angles are equal
- exterior angles are equal
Interior Angle:
Sum of the interior angles of a polygon with n sides = (n – 2) × 180°
So, each interior angles = (n – 2) × 180n
Exterior Angle:
Sum of the exterior angles of polygons = 360°
So, each exterior angle = 360°n
Sum of Interior Angle and Exterior Angle:
Whether the polygon is regular or irregular, at each vertex of the polygon sum of an interior angle and exterior angle is 180°.
Solved Examples on Polygon
Example 1: Fill in the blank.
- The name of the three sided regular polygon is ________________.
- A regular polygon is a polygon whose all _____________ are equal and all angles are equal.
- The sum of the exterior angles of a polygon is __________.
- A polygon is a simple closed figure formed by only _______________.
Solution:
- equilateral triangle
- sides
- 360°
- line segments
Example 2: Write the number of sides for a given polygon.
- Nonagon
- Triangle
- Pentagon
- Decagon
Solution:
- 9
- 3
- 5
- 10
Example 3: Find the measure of each exterior angle of a regular polygon of 20 sides.
Solution:
The polygon has 20 sides. So, n = 20.
Sum of the exterior angles of polygons = 360°
So, each exterior angle = 360°n = 360°20 = 18°
Example 4: The sum of the interior angles of a polygon is 1620°. How many sides does it have?
Solution:
Sum of the interior angles of a polygon with n sides = (n – 2) × 180°
1620° = (n – 2) × 180°
n – 2 = 1620180
n – 2 = 9
n = 9 + 2
n = 11
So, the given polygon has 11 sides.
Practice Problems on Polygon
Polygon
What is the sum of all the angles of a heptagon?
Heptagon has 7 sides. So, n = 7, Sum of the angles of a polygon = (n – 2) × 180° = (7 – 2) × 180° = 5 × 180° = 900°
What is the sum of the exterior angle of a pentagon?
The sum of exterior angles of a polygon will always be equal to 360 degrees, irrespective of the number of sides it has.
If three angles of a quadrilateral are each equal to 55°, the quadrilateral is of type:
Quadrilateral has 4 sides. So, n = 4 Sum of the angles of a polygon = (n – 2) × 180° = (4 – 2) × 180° = 2 × 180° = 360° 55° + 55° + 55° + fourth angle = 360° Measure of fourth angle = 360° - 165° = 195° So, the given quadrilateral is concave polygon as it has at least one interior angle greater than 180°.
Rhombus has all sides equal but it’s all angles are not equal.
Which of the following is not a regular polygon?
Frequently Asked Questions on Polygon
What is the diagonal of a polygon?
A diagonal of a polygon is a line segment connecting two non-consecutive vertices (corners).
What are the properties of regular polygons?
A Regular polygon has all sides of equal length and each angle also measures equal.
Is a circle a polygon?
Polygon is a closed shape made up of straight-line segments. The circle is a closed figure but it is made of a curve. So, a circle is not a polygon.
What is the minimum number of sides a polygon must-have?
A polygon must have a minimum of three sides.
Can a number of angles and the number of sides for a polygon be different?
No, polygons have the same number of sides and angles because they are closed figures with non-intersecting lines.


















