Quarter Circle

Quarter Circle – Introduction

In our everyday lives, we come across many shapes in the form of various objects, like a square table, a rectangular tray, a football in the shape of a circle, oval eggs, etc.

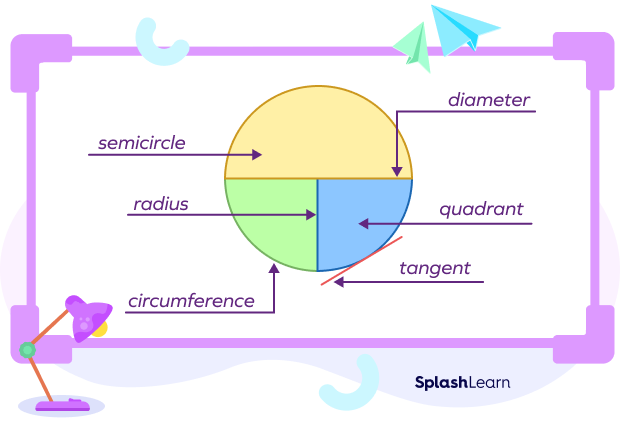
Have you ever observed the shape of a slice of pizza when divided into 4 equal parts? It looks like a triangle, but one of the sides is actually curvy. This shape is called a quarter circle.

What Is a Quarter Circle?

A quarter of anything means one-fourth of that object or thing. Thus, by a quarter of a circle, we mean one-fourth of the circle. We can also get a quarter circle by dividing a semicircle into two halves.

The following image shows division of a circle in quarters.

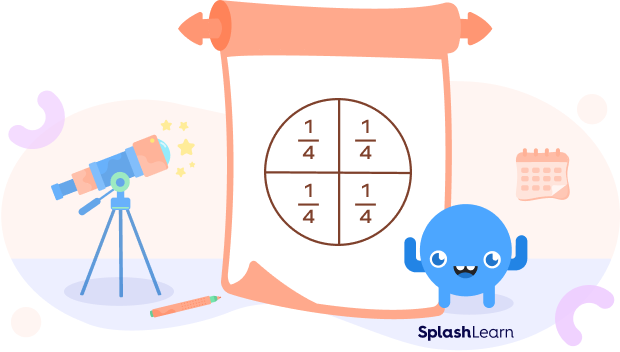
In mathematical terms, the area created by two perpendicular radii and one-fourth area of the circumference of a whole circle is called a quarter circle. It is also often referred to as a quadrant.

Area of a Quarter Circle

One-fourth area of a whole circle is known as the area of a quadrant or a quarter of a circle. 

Quarter circle formula for area can be given as:

Area of a quarter circle $=$ Area of circle $/ 4 = \frac{π\text{r}^2}{4}$

Note:

The value of $π = 22/7$ or, $3.14$

Perimeter of a Quarter Circle

The perimeter of a quarter circle consists of two radii and the circumference of a quarter circle (which is the one fourth part of the circumference of a circle). Hence, the formula for calculating it would be as follows:

Perimeter of a Quarter Circle $= \text{r} + \text{r} + (\frac{2π\text{r}}{4}) = 2\text{r} + (\frac{π\text{r}}{2})$

Solved Examples

Example 1: If the radius of a circle is 6 cm, what will be the area of a quarter of its circle?

Solution:

Area of a quadrant $= π\frac{\text{r}^2}{4}$

                                $= \frac{3.14 \times 6 \times 6}{4}$

                                $= \frac{113.04} {4}$

                                $= 28.26 \text{cm²}$

Example 2: If the diameter of a circle is 32 cm, what will be the area of a quarter circle?

Solution:

Diameter of the circle $= 32$ cm

So, radius of the circle $= \text{diameter}/2 = 32/2 = 16 \text{cm}$

Area of quadrant $= \frac{π\text{r}}{24} = \frac{3.14 \times 16 \times 16} {4} = 200.96 \text{cm²}$

Example 3: A circular park has a radius of 35 yards. One-quarter of the park has a playground for toddlers. Find the perimeter of the playground.

Solution:

The total radius of the park $(\text{r}) = 35$ yards

The perimeter of the quarter of the park $= 2\text{r} +$ $(\frac{π\text{r}}{2})$

$= 2 \times 35  + ( \frac{3.14 \times 35} {2})$

$= 70 + 54.95$

$= 124.95$ yards

Practice Problems

Frequently Asked Questions