Triangles – Definition, Properties, Types, FAQs, Examples

What are Triangles?

A triangle is a closed, 2-dimensional shape with 3 sides, 3 angles, and 3 vertices. A triangle is also a polygon. 

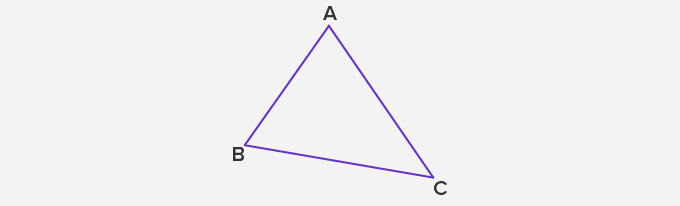
The above figure is a triangle denoted as △ABC.

Examples of Triangles

Some real-life examples of triangles include sandwiches, traffic signs, cloth hangers, and a rack in billiards.

Non-examples of Triangles

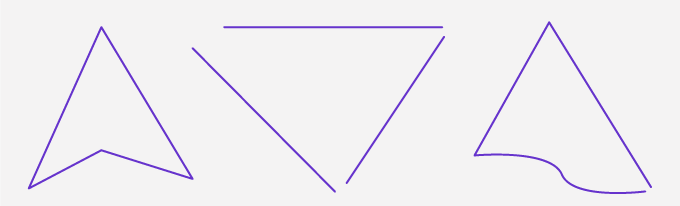
The above figures are non-examples of triangles. These shapes cannot be called triangles as –

• The first figure is four-sided.
• The second figure is an open shape.
• The third figure has a curved side.

Parts of a Triangle

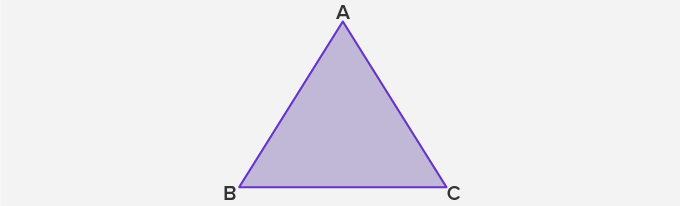
1. A triangle has 3 sides. In triangle ABC, the sides are AB, BC, and CA.
2. The angle formed by any two sides of a triangle is the angle of the triangle, denoted by the symbol ∠. A triangle has three angles.  The three angles of the triangle ABC are ∠ABC, ∠BCA, and ∠CAB. These angles are also called ∠B, ∠C, and ∠A, respectively.
3. The point of intersection of any two sides of a triangle is known as a vertex. A triangle has three vertices. In triangle ABC, the vertices are A, B, and C.

Properties of a Triangle

• The sum of all three interior angles of a triangle is always equal to 180⁰.
• The sum of the length of any two sides of a triangle is always greater than the length of the third side.
• The area of a triangle is equal to half of the product of its base and height.

Types of Triangles

Triangles can be classified based on the length of the sides or their angle measurements.

To classify triangles according to their angles, we measure each of their interior angles. Triangles can be classified by angles, as:

• Acute Triangle or Acute-angled Triangle
• Right Triangle or Right-angled Triangle
• Obtuse Triangle or Obtuse-angled Triangle

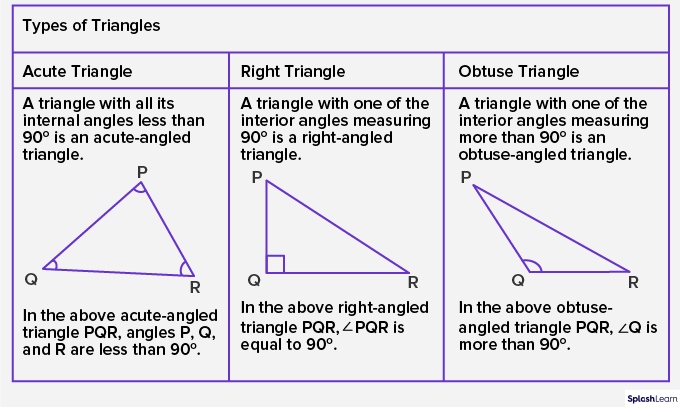
The types of triangles based on the length of the sides are –

• Scalene triangle
• Isosceles triangle
• Equilateral triangle

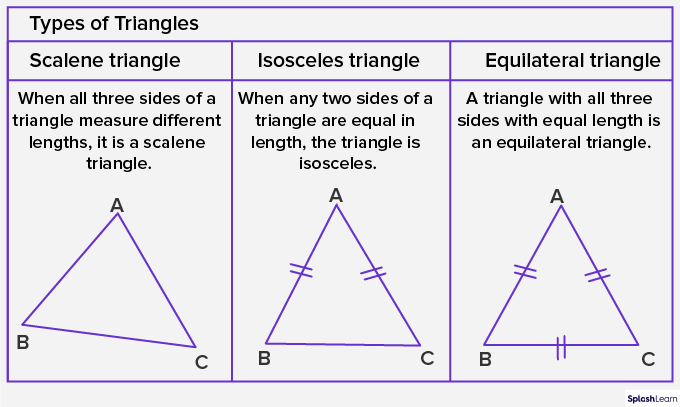
To classify triangles according to both angles and sides, we measure the interior angles and length of the sides of the triangle. Triangles classified based on both angles and sides are –

• Acute Equilateral Triangle
• Right Isosceles Triangle
• Obtuse Scalene Triangle

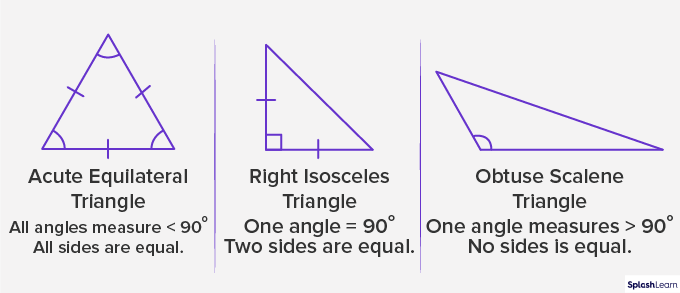
Area of a Triangle

The area of a triangle is the region that the triangle occupies in 2d space. The area of different triangles differs based on their size. If we know the base length and height of a triangle, we can determine its area. It is expressed in square units.

So, the Area of a triangle = ½ (Product of base and height of a triangle)

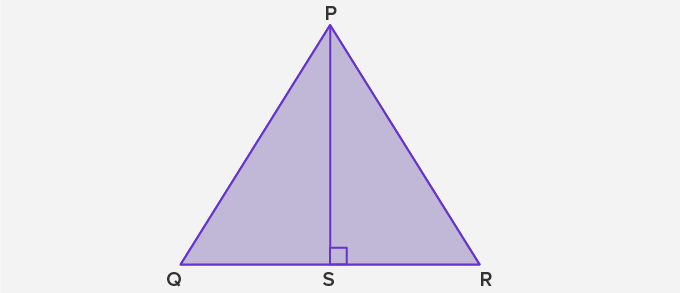
In the triangle PQR, PQ, QR, and RP are the sides. QR is the triangle’s base, and PS is the triangle’s height. PS is perpendicular from vertex P to the side QR. So, to find the area of △PQR, we use the following formula:

Area △PQR = ½ (Product of base and height of a triangle)

Or, Area △PQR = ½ (QR X PS)

The perimeter of a Triangle

The perimeter of a triangle is the sum of the length of all sides of the triangle.

So, the perimeter of the triangle = Sum of all three sides.

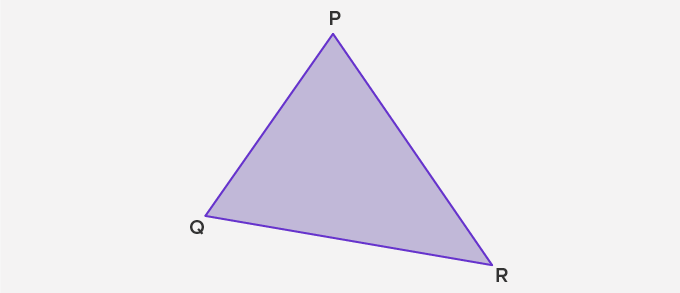
In triangle PQR, the perimeter will be the sum of the three sides, i.e., PQ, QR, and RP.

So, Perimeter of △PQR = PQ + QR + RP.

Solved Examples On Triangle

Q. Find the area of a triangle with a base equal to 10 cm and height equal to 8 cm.

Ans. For the given triangle, base = 10 cm and height = 8 cm

We know that,

Area of a triangle= ½ (Product of base and height of a triangle)

So, Area of the given triangle= ½ (10 x 8) = ½ (80) = 40 cm²

Q. Using the below figure, find the perimeter of the triangle ABC.

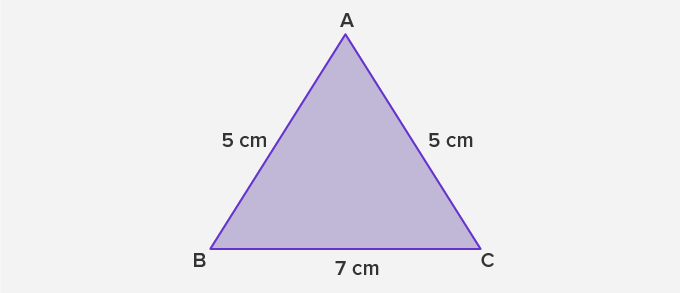
Ans. We know that, Perimeter of a triangle = (Sum of all sides of the triangle)

In the given figure, the lengths of sides of triangle ABC are

AB= 5 cm, CA= 5 cm, and BC= 7 cm.

So, Perimeter of △ABC= AB + BC + CA = 5 + 7 + 5 = 17 cm.

Q.  Identify if the given shape is a triangle or not and also give reasons.

B.

C.

Ans. A. The given figure is a triangle as it has three straight sides and is a closed figure.

B. The shape is not a triangle as it has four sides.

C. The shape is not a triangle as it is an open figure with three open sides.

Q. The perimeter of the triangle PQR is 16cm and the sides PQ and QR measure 4cm and 6cm. Find the length of the third side of the triangle.

Ans. We know that, Perimeter of a triangle = (Sum of all sides of the triangle)

So, the Perimeter of △PQR= PQ + QR + RP

16 = 4 + 6 + RP

RP= 16 – 10 = 6cm

So, the length of the third side is 6cm.

Q. Angles A and B of a triangle ABC measure 70⁰ and 60⁰, respectively. Find the third angle C.

Ans. We know that the sum of all angles of a triangle is 180⁰. 

So, ∠A + ∠B + ∠C = 180⁰

70⁰ + 60⁰ + ∠C = 180⁰

∠C = 180⁰ – 130⁰ = 50⁰

The third angle of the triangle measures 50⁰.

Q. Is it possible to form a triangle with sides measuring 2cm, 3cm, and 6cm?

Ans. To form a triangle, the sum of any two sides should always be greater than the third side.

For the given measurements, 3cm + 6cm = 9cm is greater than 2cm, 6cm + 2cm = 8cm is greater than 3cm, but 2cm + 3cm = 5cm is lesser than 6 cm. So, the given measures cannot form a triangle.

Q. If the area of a triangle is 20cm and the length of its base is 5cm, find the triangle’s height.

Ans. We know that, Area of a triangle= ½ x base x height

So, 20 = ½ x 5 x height

Height of the triangle= (20 x 2) / 5 = 8cm

Practice Problems On Triangle

Conclusion

Geometry is an important aspect of mathematics that requires in-depth learning. The concept of triangles is a fundamental topic in Geometry for young children. With interactive learning through detailed course material from SplashLearn, make your child learn about triangles, their types and properties, and practice with games and worksheets.