What is a Partial Product?
Partial means something that is incomplete or exists only in parts.
Suppose you take a pizza and cut it into slices. Each of the slices will be a partial part of the pizza.

So, what does partial product mean in math? When we say partial product, we mean breaking down large numbers into parts to find their product easily.
Let’s say you are asked to find the product of 2 and 4. You can easily say that it is 8. But if you are asked to find the product of 32 and 54, you may have to carry out some calculations. A partial product helps you multiply such numbers easily by breaking them into parts.
Let’s get familiar with partial products and how to multiply two numbers using this method.
Recommended Games
Partial Product Definition
A partial product is a product of two numbers obtained when we break the numbers into parts, multiply the parts separately and then add them together.
Partial product method is applied to multiply numbers larger than 10. In this method, we first break the numbers into parts and then multiply the parts. We add the multiplication results to find the final product.
Recommended Worksheets
Distributive Property of Multiplication
The distributive property of multiplication says that for three numbers a, b, and c, the sum of a and b, when multiplied by c, gives the same result as a and b individually multiplied by c, and then the products are added together to find the result.
So, $\text{a} \times (\text{b} + \text{c}) = \text{a} \times \text{b} + \text{a} \times \text{c}$
When we find the product of two numbers using partial products, we follow a similar process of breaking the numbers and then finding the product.

Product of Two Numbers Using the Partial Product Method
We will discuss partial product examples with two cases:
- One-digit number with a two-digit number
- Two-digit number with a two-digit number
Multiplication of a Two-Digit Number with an One-Digit Number
Using the partial products method, we can multiply a $1-$digit number with a $2-$digit number. Here, too, we apply the distributive property of multiplication.
We use the property $\text{a} \times (\text{b} + \text{c}) = \text{a} \times \text{b} + \text{a} \times \text{c}$
Suppose we have to find the product of 8 and 73.
We first expand 73 as $70 + 3$.
Now, we find the product as follows:
$8 \times (70 + 3) = 8 \times 70 + 8 \times 3 = 560 + 24 = 584$
Multiplication of a Two-Digit Number with a Two-Digit Number
When we look at the expression $(\text{a} + \text{b}) \times \text{c} = \text{a} \times \text{c} + \text{b} \times \text{c}$, we can use this to find the product of a $1-$digit number and a $2-$digit number. What if you have to find the product of two numbers with 2 digits each. What can we do?
Let’s take this expression itself
$(\text{a} + \text{b}) \times \text{c} = \text{a} \times \text{c} + \text{b} \times \text{c}$
Let’s replace “c” with $(\text{p} +\text{q})$
$(\text{a} + \text{b}) \times (\text{p} + \text{q}) = \text{a} \times (\text{p} + \text{q}) + \text{b} \times (\text{p} + \text{q})$
Now we can see that we can apply distributive property in $\text{a} \times (\text{p} + \text{q})$ and $\text{b} \times (\text{p} + \text{q})$ separately and add all of them to get the result.
$(a + b) \times (p + q) = (a \times p) + (a \times q) + (b \times p) + (b \times q)$

We can follow the given steps to multiply $2-$digit numbers using the partial product method:
Step 1: We take the numbers we want to multiply and expand or break them into parts based on their place value.
Let’s suppose we want to multiply 12 by 34. We first break each number into parts based on its place value.
So, $12 = 10 + 2$ and $34 = 30 + 4$
Step 2: We multiply each part of the expanded form of a number with each part of the expanded form of the other number. Here, each part maintains its place.
Just like we do it in the area model of multiplication, we break the numbers into smaller parts and multiply each part with each other.
Continuing with our example,
$12 \times 34 = (10 + 2) \times (30 + 4)$
We multiply the expanded parts of the number, as shown in the image:
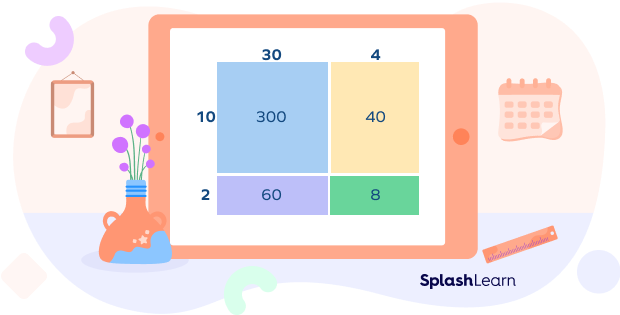
Step 3: We calculate the products of the parts and add them to find the final product of the multiplication problem.
So, $(10 \times 30) + (10 \times 4) + (2 \times 30) + (2 \times 4) = 300 + 40 + 60 + 8 = 408$
Fun Fact!
While the word “partial” indicates a part of something, it may not always do so. Partial is also used to indicate bias or favor of one side over another.
Conclusion
We learnt about the method of partial product to multiply two numbers easily along with definition, properties and fun facts. Learn and explore more at SplashLearn.
Solved Examples
1. Multiply 84 and 36 using the partial products multiplication method.
Solution: We have to multiply 84 and 36.
We expand 84 and 36.
$84 \times 36 = (80 + 4) \times (30 + 6)$
We multiply each part of the expanded form by 84, with each part of the expanded form of 36.
$= (80 \times 30) + (80 \times 6) + (4 \times 30) + (4 \times 6)$
We calculate the products and add them.
$= 2400 + 480 + 120 + 24 = 3024$
2. The size of a banner is $30 \times 40$ feet. The banner is increased in size by 3 feet in both length and width. What would be the area of the banner?
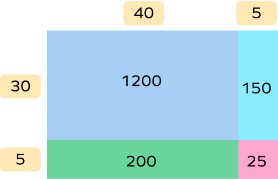
Area of the new banner $=$ Sum of partial products $= 1200 + 150 + 200 + 25 = 1575$
3. Find the missing numbers.
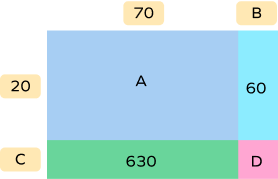
$\text{A} = 20 \times 70 = 1400$
$\text{B} = 60 \div 20 = 3$
$\text{C} = 630 \div 70 = 9$
$\text{D} = \text{C} \times \text{B} = 9 \times 3 = 27$
Practice Problems
Partial Product
Which of the following is the correct set of partial products for $15 \times 51$?
$15 \times 51 = (10 + 5) \times (50 + 1)$
$= (10 \times 50) + (10 \times 1) + (5 \times 50) + (5 \times 1)$
$= 500 + 10 + 250 + 5$
A carpet measures 11 feet $\times$ 13 feet. The carpet is increased by adding new fabric and now measures 4 feet longer and 2 feet wider. What is the area of the new carpet?
$13 \times 17 = (10 + 3) \times (10 + 7)$ $= (10 \times 10) + (10 \times 7) + (3 \times 10) + (3 \times 7)$ $= 100 + 70 + 30 + 21 = 221$ sq. feet
Find the missing numbers.
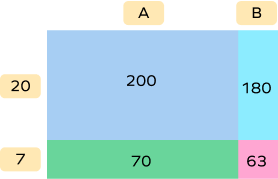
$\text{A} = 200 \div 20 = 10$
$\text{B} = 180 \div 20 = 9$
Frequently Asked Questions
Place value helps us understand each digit’s position in a number and expand them to break down numbers. Example: $27 = 20 + 7, 358 = 300 + 50 + 8$
Can we use the partial products method to multiply two algebraic expressions?
Yes. Let’s take an example:
$(2x + 3y) × (3x + 7y) = (2x \times 3x) + (2x \times 7y) + (3y \times 3x) + (3y \times 7y),$
where all the four individual products are the partial products.
Can we use the partial products method to find the product of three-digit and four-digit numbers?
Yes, the partial products method can be used to find the product of three-digit and four-digit numbers as well. We break the numbers according to place value and follow the same steps. Let’s take an example of multiplying 315 and 241:
$315 = 300 + 10 + 5$
$241 = 200 + 40 + 1$
Using the area model,
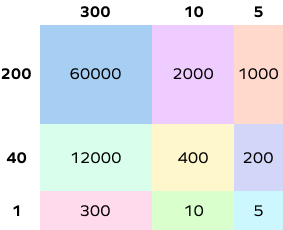
Product of $315$ and $241 =$ Sum of partial products
$315 \times 241 = 60000 + 12000 + 300 + 2000 + 400 + 10 + 1000 + 200 + 5 = 75,915$




































