What Is Two Point Form in Math?
Two point form in math is one of the important methods to find the equation of a line when coordinates of any two points on the line are known. The equation of a line is used to represent each and every point on the line, we can say that it is satisfied by each point on the line.
Let $A(x_1,\; y_1)$ and $B (x_2,\; y_2)$ be any two distinct points on the line l.
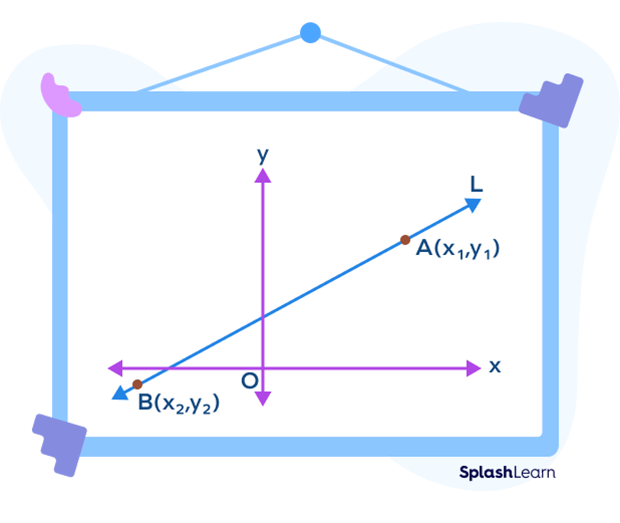
The two-point form is given by
$\frac{y\;-\;y_1}{x\;-\;x_1} = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$
Two Point Form: Definition
If $(x_1,\; y_1)$ and $(x_2,\; y_2)$ be the coordinates of any two distinct points on the line, then the equation of line in two-point form is
$\frac{y\;-\;y1}{x\;-\;x_1} = \frac{y2\;-\;y_1}{x_2\;-\;x_1}$
OR
$(y\;-\;y_2) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_2)$
Recommended Games
Two Point Form Formula
The two points formula of two point form of an equation is given as-
Let $(x_1,\; y_1)$ and $(x_1,\; y_1)$ be the two points such that the equation of line passing through these two points is given by the formula mentioned below-
$(y\;-\;y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
Here, $(x,\; y)$ is just an arbitrary point on the line.
Recommended Worksheets
Derivation of Two Point Form Formula
Let $M (x_1,\; y_1)$ and $N (x_2,\; y_2)$ be the two given points on the line L.
Let $P (x,\; y)$ be a random point on the line L.
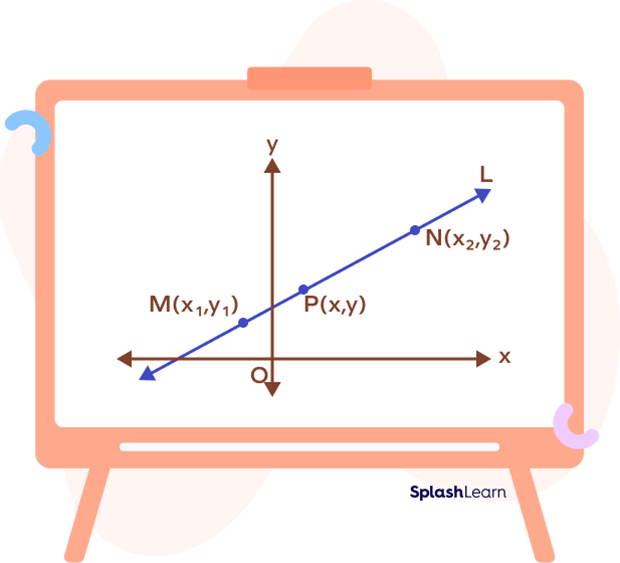
From the figure, we can observe that the three points $P_1,\; P_2$ and P lie on the same line. They are collinear.
Slope of line MP $=$ Slope of line NP
$\frac{y\;-\;y1}{x\;-\;x1} = \frac{y2\;-\;y1}{x2\;-\;x1}$
Or
$(y\;-\;y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
Equation of a Line in Two-Point Form
The equation of a line in the two-point form is given by
$(y\;-\;y1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
or
$(y\;-\;y_2) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_2)$
where
$(x,\; y)$: coordinates of any point on a line
$(x_1,\; y_1)$ and $(x_2,\; y_2)$: coordinates of two points on the line
How To Write Equation of a Line in Two Point Form
Let’s understand the steps to find the equation of a line using two-point form.
- Name the coordinates of the given two points as $(x_1,\; y_1)$ and $(x_2,\; y_2)$.
- Substitute the values in the Two-Point formula given by
$(y \;-\; y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
- Simplify.
Finding Equation of a Line Using Two Point Form
To write equation of a line in two-point form, simply substitute the coordinates of the given two points in the equation $(y\;-\;y_2) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_2)$.
Example: Find the equation of a line passing through the points $(1,\; 2)$ and $(3,\; 4)$.
Here, $(x_1,\; y_1) = (1,\; 2)$
$(x_2,\; y_2) = (3,\; 4)$
Substitute the values in $(y\;-\;y_2) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_2)$.
$(y\;-\;4) = \frac{4\;-\;2}{3\;-\;1} (x\;-\;3)$
$(y\;-\;4) = (x\;-\;3)$
$y = x + 1$
Deriving Two Point Form Using Point Slope Form
Let $A (x_1,\; y_1)$ and $B (x_2,\; y_2)$ be two given distinct points on a line as given below:
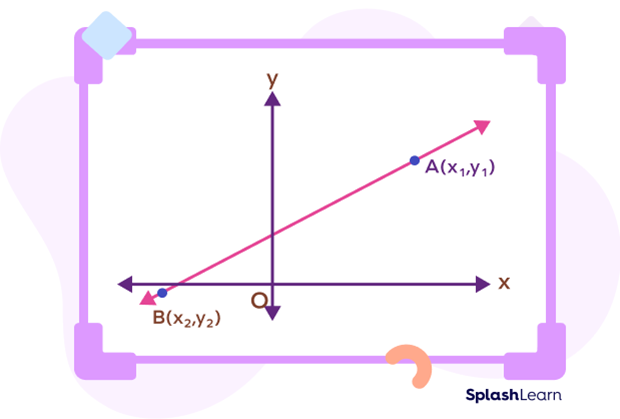
The two-point slope form of the straight line passing through these points is given by “m”:
$m = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$ __________(1)
The Point-Slope form equation of a line is given by:
$(y\;-\;y_1) = m (x\;-\;x_1)$
Substituting 1 in 2:
$(y\;-\;y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
Facts about Two Point Form!
- The two-point form of a line can also be written as given:
$\frac{y\;-\;y_1}{x\;-\;x_1} = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$
Or
$\frac{y\;-\;y_2}{x\;-\;x_2} = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$
- An exceptional case where the two-point form cannot be used is the equation of a vertical line passing through point (a, b) given by $x = a$. Slope of the vertical line is not defined.
Conclusion
In this article, we learned about two-point forms of a line. Let us now look at some examples and practice some problems to understand the concept better.
Solved Examples On Two Point Form
1. Find the equation of the line passing through the points:
$(\;-\;2,\; 3)$ and $(3,\; 5)$.
Solution:
The given points are:
$(x_1,\; y_1) = (2,\; 3)$ and $(x_2,\; y_2) = (3,\; 5)$
The equation of a straight line passing through the points $(x_1,\; y_1)$ and $(x_2,\; y_2)$ can be written using two-point form as:
$(y\;-\;y_2)= \frac{y_2\;-\;y_1}{x_2\;-\;x_1}(x\;-\;x_2)$
Substituting the values, we get:
$(y\;-\;3) = \frac{5\;-\;3}{3\;-\;(\;-\;2)}(x\;-\;2)$
$(y\;-\;3)= \frac{2}{5} (x\;-\;2)$
$5 (y\;-\;3) = 2 (x\;-\;2)$
$5y \;–\; 15 = 2x + 4$
$2x + 4 \;–\; 5y + 15 = 0$
$2x \;–\; 5y + 19 = 0$
Therefore, this is the required equation of a line passing through the given points.
2. What is the equation of a straight line passing through the points (3, 0) and (0, 3)?
Solution:
Let’s write the coordinates as
$(x_1,\; y_1) = (3,\; 0)$ and $(x_2,\; y_2) = (0, 3)$
The equation of a straight line passing through the points $(x_1,\; y_1)$ and $(x_2,\; y_2)$ can be written as:
$(y\;-\;y2) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_2)$
Substituting the values, we get
$(y\;-\;0) = \frac{3\;-\;0}{0\;-\;3} (x\;-\;3)$
$y = \frac{3\;-\;}{3} (x\;-\;3)$
$y =\;-\;1(x \;–\; 3)$
$y =\;-\;x + 3$
$x + y \;–\; 3 = 0$
Therefore, the equation of a line passing through the given points $(3,\; 0)$ and $(0,\; 3)$ is $x + y \;–\; 3 = 0$
3. Find the equation of a line with two points $(3,\; 5)$ and $(2,\; 3)$.
Solution:
Given : Two points on the straight line are $(3,\; 5)$ and $(2,\; 3)$.
The equation of a straight line passing through the points $(x_1,\; y_1)$ and $(x_2\;, y_2)$ can be written as:
$(y \;-\; y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
Substitute $(x_1,\; y_1) = (3,\; 5)$ and $(x_2,\; y_2) = (2,\; 3)$
$(y\;-\;5) = \frac{3\;-\;5}{2\;-\;3} (x\;-\;3)$
$(y\;-\;5) =\frac{\;-2}{\;-1} (x\;-\;3)$
$y\;-\;5 = 2(x\;-\;3)$
$y\;-\;5 = 2x\;-\;6$
$2x\;-\;y = 6\;-\;5$
$2x\;-\;y = 1$
$2x \;-\; y \;-\;1 = 0$
4. Find the equation of a straight line whose x-intercept is “a” and y-intercept is “b.”
Solution: The line passes through the points $(a,\; 0)$ and $(0,\; b)$.
Substituting the values $(x_1,\; y_1) = (a,\; 0)$ and $(x_2,\; y_2) = (0,\; b)$ in the two point form we get
$(y\;-\;y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
$(y\;-\;0) = \frac{b\;-\;0}{0\;-\;a} (x\;-\;a)$
$y = \frac{b}{-a} (x\;-\;a)$
$-ay = b(x \;-\; a)$
$-ay = bx \;-\; ba$
$bx + ay = ab$
Dividing both sides by ab, we get:
$\frac{bx + ay}{ab} = \frac{ab}{ab}$
$\frac{x}{a} + \frac{y}{a} = 1$
Thus, the equation of the given line is given as:
$\therefore \frac{x}{a} + \frac{y}{a} = 1$
This is also known as the intercept-form of a line.
5. Derive the y-intercept of the line with the coordinates given by: $A\; (3, \;-\;2)$ and B $(\;-\;1,\; 3)$ passing through it and also find the slope m of the line.
Solution:
Let the given points be:
$(x_1,\; y_1) = ( 3,\;-\;2)$
$(x_2,\; y_2) = (\;-\;1, 3)$
The equation of a straight line passing through the points $(x_1,\; y_1)$ and $(x_2,\; y_2)$ can be written as:
$(y \;-\; y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_1)$
$(y\;-\;(\;-\;2)) = \frac{3\;-\;(\;-\;2)}{\;-\;1\;-\;3} (x\;-\;(\;-\;1))$
$(y + 2) = \frac{5}{-\;4} (x + 1)$
Now, multiplying both sides by $-4$ gives us,
$\;-4 (y + 2) = 5 (x + 1)$
$\;-4y \;–\; 8 = 5x + 5$
$\;-4y = 5x +13$
$5x +4y +13 =0$
$y = \frac{-5}{4}x + \frac{13}{4}$
The line equation from two points is given above.
The final equation of the slope-intercept form is written as-
$y = mx + b$
Comparing our equation to the standard form, we will get y-intercept, b as $\frac{7}{4}$.
Further, the slope of the line (m) can be given as $\frac{-5}{4}$.
Practice Problems On Two Point Form
Two Point Form – Definition, Derivation, Formula, Examples
What is the equation of the line in the slope point form?
The equation of a straight line passing through the points $(x_1,\; y_1)$ and $(x_2,\; y_2)$ can be written using two-point form as $(y\;-\;y_1) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}(x\;-\;x_1)$
What is the equation of a straight line passing through the points (5, 0) and (0, 5)?
Substitute $(x_1,\; y_1) = (5,\; 0)$ and $(x_2,\; y_2) = (0,\; 5)$ in the two point form.
$(y\;-\;y_2) = \frac{y_2\;-\;y_1}{x_2\;-\;x_1} (x\;-\;x_2)$
Substituting the values, we get;
$(y\;-\;0) = \frac{5\;-\;0}{0\;-\;5} (x\;-\;5)$
$y = \frac{5}{-5} (x\;-\;5)$
$y = (\;-\;1)(x \;–\; 5)$
$y = \;-x + 5$
$x + y \;– 5 = 0$
Therefore, the equation of a line passing through the given points $(5,\; 0)$ and $(0,\; 5)$ is $x + y \;–\; 5 = 0$
What is the slope of a line passing through the points $(\;-5,\; 4)$ and $(3,\; -2)$.
The slope of a straight line passing through the points $(x_1,\; y_1)$ and $(x_2,\; y_2)$ can be written as:
Slope $= \frac{y_2\;-\;y_1}{x_2\;-\;x_1}$
Substitute $(x_1,\; y_1) = (\;-\;5,\; 4)$ and $(x_2,\; y_2) = (3,\; \;-\;2)$
Slope $= \frac{-2\;-\;4}{3 + 5} = \frac{-3}{4}$
What is the equation of a vertical line passing through the point $A (\;-3,\; \;-5)$?
The equation of a vertical line passing through the point $(a,\; b)$ is $x = a$.
The equation of a vertical line passing through the point $A\; (\;-3,\; -5)$ is $x = \;-3$.
Frequently Asked Questions On Two Point Form
How do you determine whether a point lies on a line?
Every point on a line satisfies its line equation. For example, to see whether (3, 6) lies on a line $y = 2x$, we substitute $x = 3$ and $y = 6$ in the given equation. Then we get: $6 = 2(3)$ or, $6 = 6$. The equation is satisfied and hence the point (3, 6) lies on the line $y = 2x$.
What is the point slope form?
The equation of line in point slope form is given by $y \;-\; y_1 = m (x \;-\; x_1)$.
What is the equation of x-axis?
The equation of x-axis is $y = 0$.
What is the equation of y-axis?
The equation of y-axis is x = 0.




































