What Is the Area of a Pentagon?
A pentagon is a polygon having five sides and 5 angles. The Greek word “penta” means “five” and “gon” means “angles.” The area of a pentagon is the region bounded by the five sides of the pentagon.
In the image below, we can see that the area of the pentagon is shaded in black color.
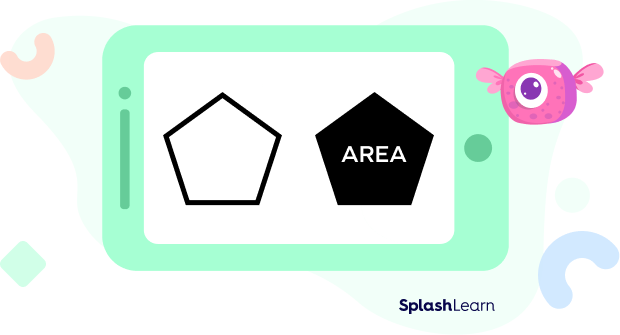
The area of a pentagon is the region that is enclosed within the five sides of a pentagon. There are many methods for calculating the area of a pentagon depending upon the dimensions that are known to us. The type of pentagon also plays a major role in calculating the area.
The area of a regular pentagon can be calculated with the help of a fixed formula, but if we have an irregular pentagon, then we need to break it down into multiple different polygons and sum up their areas to get the area of the pentagon.
The area of a pentagon is expressed in “square units,” like $cm^2,\; in^2,\; m^2,\; ft^2$, etc.
Recommended Games
Area of a Pentagon Formula
There are many methods and formulas to find the area of a pentagon and it varies according to the type of the pentagon. The most commonly used formula for the area of a pentagon is
$Area\; of\; a\; Pentagon = \frac{1}{2} \times Perimeter \times Apothem$
$= \frac{1}{2} \times p \times a$
“p” is the perimeter of the pentagon.
“a” is the apothem of the pentagon.
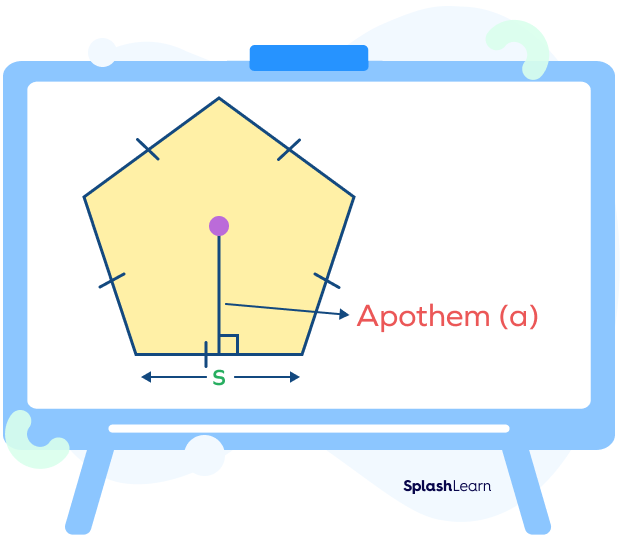
Note: An apothem of a regular polygon is a perpendicular drawn from the center to the midpoint of any of its sides.
Recommended Worksheets
How to Find the Area of a Pentagon
We can calculate the area of a pentagon using different methods and formulas, depending on the values that are given and also the type of pentagon.
- Area of Regular Pentagon
- Area of Pentagon with Apothem
- Area of Irregular Pentagon
Area of Regular Pentagon
A regular pentagon is a pentagon in which all the sides are equal and all angles are of equal measures. The area of a regular pentagon can be calculated only if the side length “s” is known to us.
The formula used to find the area of a regular pentagon is:
Area of regular pentagon$= \frac{1}{4}\sqrt{5 ( 5 + 2\sqrt{5} )}\;s^2$
“s” : the length of the side of the regular pentagon.
Example: Find the area of a regular pentagon whose side is 5 units.
Solution:
Area of regular pentagon $= \frac{1}{4}\sqrt{5( 5 + 2\sqrt{5})}\;s^2$
Given $s = 5$.
After substituting the value of $s = 5$, we get
$\frac{1}{4}\sqrt{5 ( 5 + 2\sqrt{5})}\;s^2 = \frac{1}{4}\sqrt{25 + 105)} \times 25 = 43.011$ square units.
Note:
The term $\frac{1}{4}\sqrt{5 ( 5 + 2\sqrt{5})}$ in the formula equals 1.7204774006.
To find an estimate, we can use $\frac{1}{4}\sqrt{5(5+2\sqrt{5})} \simeq 1.72$
We may not get accuracy till the last decimal point, but the answer will be very close to the actual result.
Thus, the formula can be written as:
Area of a regular pentagon with side “s” $= 1.72\; s^2$
Area of Pentagon with Apothem
If we know the side and apothem of a pentagon, the area of a pentagon can be calculated by the formula
Area of regular polygon$= \frac{1}{2} \times Perimeter\; of\; polygon\; \times Apothem$
Area of regular pentagon$= \frac{1}{2} \times p \times a$
where “p” is the perimeter of the pentagon and “a” is the apothem of the pentagon.
Example: Find the area of a regular pentagon whose side length is 12 units and the length of apothem is 3 units.
Solution:
$s = 12$ units and $a = 3$ units.
Perimeter of pentagon $= 5 \times side\; length\; = 5 \times 12 = 60$ units.
Area of the pentagon, $A = \frac{1}{2} \times p \times a$
Substitute $p = 60,\; a = 3$
$\Rightarrow A = \frac{1}{2} \times 60 \times 3$
$\Rightarrow A = 90$ square units
Therefore, the area of the pentagon is 90 square units.
Area of an Irregular Pentagon
If we have an irregular pentagon, we can calculate its area by dividing the pentagon into smaller polygons such as rectangles, triangles. We calculate the area of these polygons and add them together to get the area of the pentagon.
Example: Find the area of a given irregular pentagon.
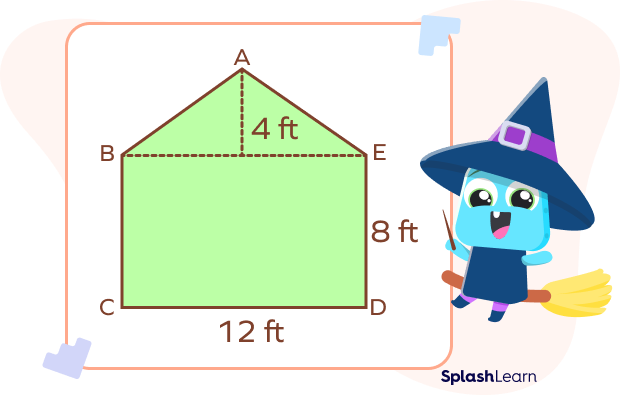
Solution: The given pentagon can be divided into a triangle and a rectangle.
Area of triangle $= \frac{1}{2} \times Base \times Height$
$= \frac{1}{2}\times 12 \times 4$
$= 24$ square feet
Area of rectangle $= Length\times Width$
$= 12 \times 8$
$= 96$ square feet
Area of given irregular pentagon $= Area\; of\; triangle + Area\; of\; rectangle$
$= 24 + 96$
$= 120$ square feet
Facts about Area of Pentagon
- The sum of all the interior angles of a regular pentagon is equal to $540^\circ$.
- In a regular pentagon, each interior angle is equal to 108° and each exterior angle is equal to $72^\circ$.
Conclusion
In this article, we learned how to find the area of a pentagon. We discussed three methods to find the area of the pentagon. Let us solve a few examples and practice problems for better understanding.
Solved Examples on Area of Pentagon
1. Find the area of the regular pentagon with side $= 8$ feet?
Solution:
We know that the formula to calculate the area of a regular pentagon is,
Area of regular pentagon $= \frac{1}{4} \sqrt{5 (5 + 2\sqrt{5})}\;s^2$
side $(s) = 8\; ft$
Putting the value in the above formula:
$Area = \frac{1}{4}\sqrt{5 (5 + 2\sqrt{5})}\;s^2$
$= \frac{1}{4} \times 64 \times 6.882$
$= 110.112\;ft^2$.
Therefore, the area of the pentagon of side 8 is $110.112\;ft^2$.
2. Calculate the area of a regular pentagon given that the length of the side of the pentagon is 10 feet and the length of the apothem is 7 feet.
Solution:
Given, $s = 10$ and $a = 7$ .
The formula to calculate the area of a pentagon with apothem is:
Area of pentagon $= \frac{1}{2} \times perimeter \times apothem$.
Let us calculate the perimeter of the pentagon.
Perimeter of the pentagon $= 5 \times side length = 5 \times 10 = 50$ feet
Now, let us put these values in the above formula.
Area of pentagon $= \frac{1}{2} \times p \times a$
$\Rightarrow A = \frac{1}{2} \times 50 \times 7$
$\Rightarrow A = 175\;feet^2$
Therefore, the area of the pentagon is 175 square feet.
3. Find the length of the apothem of the pentagon if the area of a pentagon is 600 square feet and side length is 12 feet.
Solution:
Area of pentagon $= 600$ units feet
$s = 12$ feet
Perimeter of pentagon$= p = 5 \times side\; length = 5 \times 12 = 60$ units
Using the formula for the area of a pentagon,
Area of pentagon $= \frac{1}{2} \times p \times a$
$\Rightarrow 600 = \frac{1}{2} \times 60 \times a$
$\Rightarrow a = \frac{600}{30}$
$\Rightarrow a = 20$ units
Therefore, the length of the apothem is 20 units.
4. Find the area of the given pentagon.
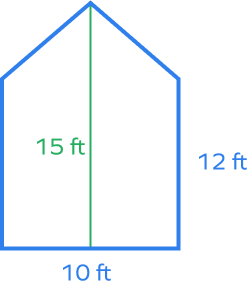
Solution:
Divide the pentagon into a rectangle and a triangle.
Area of triangle $= \frac{1}{2} Base \times Height = \frac{1}{2}\times10\times3 = 15$ square feet
Area of rectangle $= Length \times Width = 10\times12 = 120$ square feet
Area of given pentagon $= Area \;of \;triangle + Area\; of\; rectangle$
$= 15 + 120$
$= 135$ square feet
Practice Problems on Area of a Pentagon
Area of a Pentagon - Definition, Formula, Examples, FAQs
The area of a pentagon can be calculated using
Area of pentagon is given by $12 \times perimeter \times apothem$.
Perimeter of the pentagon $= 75$ feet
Length of the apothem $= 10$ feet
Find the area.
Here, $p = 75$ feet and $a = 10$ feet
Area of pentagon$= 12 \times perimeter \times apothem$
$\Rightarrow A = 12 \times 75 \times 10$
$Rightarrow A = 375\;feet^2$
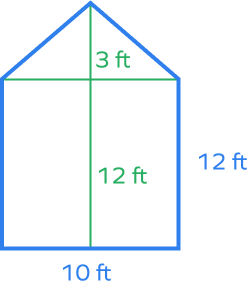
What is the area of the given irregular pentagon?
Height of the triangle $= 18\;in\;-\;12\;in = 6\;in$
Area of triangle $= \frac{1}{2}$ BaseHeight $= \frac{1}{2}\times10\times6 = 30$ square feet
Area of rectangle $= Length \times Width = 10\times12 = 120$ square feet
Area of given irregular pentagon $= Area\; of \;triangle + Area\; of\; rectangle$
$= 30 + 120$
$= 150$ square feet
Frequently Asked Questions on Area of a Pentagon
What are the different types of pentagon?
There are four types of pentagons:
- Concave Pentagon
- Convex Pentagon
- Regular Pentagon
- Irregular Pentagon
What is a concave pentagon?
A pentagon in which there is at least one angle which is more than 180° is known as a concave pentagon.
What is a convex pentagon?
A pentagon in which every angle is less than 180° is known as a convex pentagon.
What is the name of a polygon with 6 sides?
A polygon with six sides is known as a hexagon.