Cube Numbers – Definition, Examples, Facts, Practice Problems

What Are Cube Numbers?

We know that a “number squared” refers to the product of the number with itself. So, to find a square, we simply multiply the number with itself once.

What is a cubed number? A “number cubed” refers to the multiplication of the number with itself and again by itself, i.e., multiplication of the same number two times.

In other words, we can find the cube of a number by multiplying the square of a number by the number itself.

A cube number is obtained by raising a given number to the power of 3. 

Thus, for a given number n, the cube number is “n cubed” or “$n^3$.”

Cube Numbers Definition

A cube number is the result of the product of three identical numbers.

A cube number is the number raised to the power of 3. 

A cube number is the result of multiplication of a number with itself twice.

n cubed $=n^3=n\times n\times n$

Cube numbers of positive numbers are positive. 

Cube numbers of negative numbers are negative.

Examples of cube numbers:

$(-2{)}^3=(-2)\times (-2)\times (-2)=-8$

$6^3=6\times 6\times 6=216$

${10}^3=10\times 10\times 10=1000$

$(-10{)}^3=(-10)\times (-10)\times (-10)=-1000$

Why Are They Called Cube Numbers?

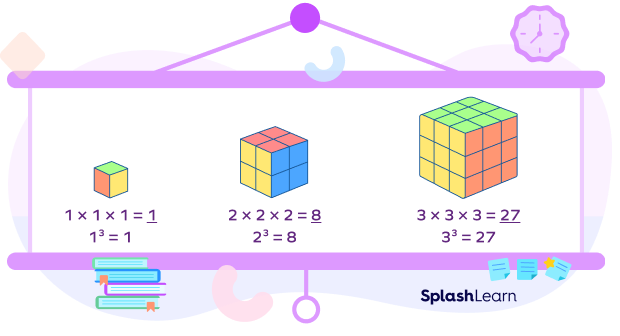
The best example of a cube number in geometry is the volume of a cube.

A cube is a three-dimensional shape or a geometric solid. All its sides are equal in length. 

The volume of a cube with side “s” is given by $s^3$ or “side cubed.”

Volume of a cube with side 1 unit $=1^3=1$

Volume of a cube with side 2 units $=2^3=8$

Volume of a cube with side 3 units $=3^3=27$

and so on.

Since a cube is a three-dimensional shape with the same length, width, and height of its sides, its volume can be calculated by “cubing” its length.

A cube with side-length 1 unit is called a unit cube. If “n” such unit cubes perfectly fit inside a given cube, then we say that the volume of a given cube is “n cubic units.”

List of Cube Numbers From 1 to 100

1	1	$1\times 1\times 1$	51	132651	$51\times 51\times 51$
2	8	$2\times 2\times 2$	52	140608	$52\times 52\times 52$
3	27	$3\times 3\times 3$	53	148877	$53\times 53\times 53$
4	64	$4\times 4\times 4$	54	157464	$54\times 54\times 54$
5	125	$5\times 5\times 5$	55	166375	$55\times 55\times 55$
6	216	$6\times 6\times 6$	56	175616	$56\times 56\times 56$
7	343	$7\times 7\times 7$	57	185193	$57\times 57\times 57$
8	512	$8\times 8\times 8$	58	195112	$58\times 58\times 58$
9	729	$9\times 9\times 9$	59	205379	$59\times 59\times 59$
10	1000	$10\times 10\times 10$	60	216000	$60\times 60\times 60$
11	1331	$11\times 11\times 11$	61	226981	$61\times 61\times 61$
12	1728	$12\times 12\times 12$	62	238328	$62\times 62\times 62$
13	2197	$13\times 13\times 13$	63	250047	$63\times 63\times 63$
14	2744	$14\times 14\times 14$	64	262144	$64\times 64\times 64$
15	3375	$15\times 15\times 15$	65	274625	$65\times 65\times 65$
16	4096	$16\times 16\times 16$	66	287496	$66\times 66\times 66$
17	4913	$17\times 17\times 17$	67	300763	$67\times 67\times 67$
18	5832	$18\times 18\times 18$	68	314432	$68\times 68\times 68$
19	6859	$19\times 19\times 19$	69	328509	$69\times 69\times 69$
20	8000	$20\times 20\times 20$	70	343000	$70\times 70\times 70$
21	9261	$21\times 21\times 21$	71	357911	$71\times 71\times 71$
22	10648	$22\times 22\times 22$	72	373248	$72\times 72\times 72$
23	12167	$23\times 23\times 23$	73	389017	$73\times 73\times 73$
24	13824	$24\times 24\times 24$	74	405224	$74\times 74\times 74$
25	15625	$25\times 25\times 25$	75	421875	$75\times 75\times 75$
26	17576	$26\times 26\times 26$	76	438976	$76\times 76\times 76$
27	19683	$27\times 27\times 27$	77	456533	$77\times 77\times 77$
28	21952	$28\times 28\times 28$	78	474552	$78\times 78\times 78$
29	24389	$29\times 29\times 29$	79	493039	$79\times 79\times 79$
30	27000	$30\times 30\times 30$	80	512000	$80\times 80\times 80$
31	29791	$31\times 31\times 31$	81	531441	$81\times 81\times 81$
32	32768	$32\times 32\times 32$	82	551368	$82\times 82\times 82$
33	35937	$33\times 33\times 33$	83	571787	$83\times 83\times 83$
34	39304	$34\times 34\times 34$	84	592704	$84\times 84\times 84$
35	42875	$35\times 35\times 35$	85	614125	$85\times 85\times 85$
36	46656	$36\times 36\times 36$	86	636056	$86\times 86\times 86$
37	50653	$37\times 37\times 37$	87	658503	$87\times 87\times 87$
38	54872	$38\times 38\times 38$	88	681472	$88\times 88\times 88$
39	59319	$39\times 39\times 39$	89	704969	$89\times 89\times 89$
40	64000	$40\times 40\times 40$	90	729000	$90\times 90\times 90$
41	68921	$41\times 41\times 41$	91	753571	$91\times 91\times 91$
42	74088	$42\times 42\times 42$	92	778688	$92\times 92\times 92$
43	79507	$43\times 43\times 43$	93	804357	$93\times 93\times 93$
44	85184	$44\times 44\times 44$	94	830584	$94\times 94\times 94$
45	91125	$45\times 45\times 45$	95	857375	$95\times 95\times 95$
46	97336	$46\times 46\times 46$	96	884736	$96\times 96\times 96$
47	103823	$47\times 47\times 47$	97	912673	$97\times 97\times 97$
48	110592	$48\times 48\times 48$	98	941192	$98\times 98\times 98$
49	117649	$49\times 49\times 49$	99	970299	$99\times 99\times 99$
50	125000	$50\times 50\times 50$	100	1000000	$100\times 100\times 100$

How to Cube Numbers

To cube numbers, simply multiply the square of a number by itself.

The standard form of a cube of any number “a” is “$a^3$,” which can be obtained using $a^3=a\times a\times a$. This applies to every number. 

For example, $3\times 3\times 3=27,8\times 8\times 8=512,10\times 10\times 10=1000$, etc.

Cube Numbers vs. Square Numbers

The cube numbers are the numbers obtained by raising a number to the power of 3, whereas a square is obtained by multiplying a number by itself.

Square of $n=n^2=n\times n$  …a number multiplied by itself once

Cube of $n=n^3=n\times n\times n$ …a number multiplied by itself twice

Let us consider an example. 

Multiply 4 by itself to get its square.

4 squared $=4^2=4\times 4=16$ …4 multiplied by itself once

Multiplying 42 by 4, we get

4 cubed $=4^3=4\times 4\times 4=64$ …4 multiplied by itself twice

Here, 64 is a cube number. 

Cube Numbers in Real Life

While cube numbers are excellent for assisting students in comprehending patterns and relationships between numbers, they also have practical applications. Let’s say we want to know the volume of a cubic object like a container; all we need to do is cube the value of one of its sides.

To determine the dimensions of gift boxes, size of ice cubes, etc., are a few of the many real-life uses for cube numbers.

Facts about Cube Numbers

Conclusion

In this article, we have learned about cube numbers, their visualization, list, and examples. Let’s solve a few examples and practice problems.

Solved Examples on Cube Numbers

1. Find out the cube of numbers $9,-15$, and 19.

Solution:

Cube of numbers 9, 15, and 19 calculated as

$9^3=9\times 9\times 9=929$

$(-15{)}^3=(-15)\times (-15)\times (-15)=3375$

${19}^3=19\times 19\times 19=6859$

2. Evaluate ${25}^3$.

Solution:

${25}^3=25\times 25\times 25$

      $=625\times 25$

      $=15625$

3. Write the cube number 64 and 125 as the sum of the consecutive odd numbers.

Solution:

64 and 125 as the sum of the consecutive odd numbers can be written as 

$64=1+3+5+7+9+11+13+15$

$125=21+23+25+27+29$.

4. If the side length of a cube is 12 units, find its volume.

Solution:

The volume of a cube can be calculated by “cubing” its side length.

The side length of a cube $=12$ units

$\therefore$ Volume $={12}^3=12\times 12\times 12$

 $=1728$ cubic units.

5. Explain why the number 512 is a cube number.

Solution:

The number 512 can be written as $512=8\times 8\times 8$.

Here, the result of multiplying the number 8 by itself and then by itself again is 512.

And a cube number is defined as the result of multiplying a number by itself and then by itself again. Thus, 512 is a cube number.

Practice Problems on Cube Numbers

Frequently Asked Questions on Cube Numbers