What Is the Segment Addition Postulate in Geometry?
The segment addition postulate states that if three points A, B, and C are collinear such that B lies between A and C, then the sum of the lengths of segment AB and segment BC is equal to the length of the entire segment AC.
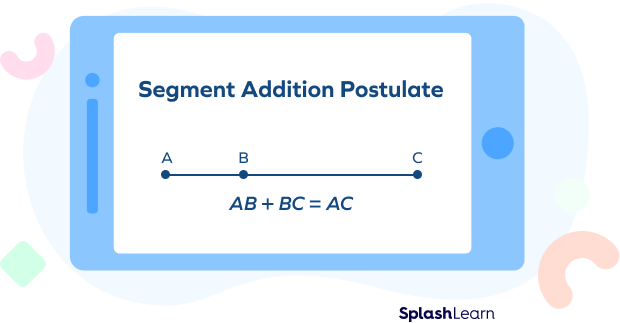
The segment addition postulate (segment addition theorem), in simple words, states that if we divide a line segment into smaller segments, the sum of lengths of the smaller segments will add up to the length of the original segment. It is applicable to the line segments.
The segment addition postulate is an important property of line segments that is used to check if three points are collinear or whether a point lies on a given segment or not.
Recommended Games
Segment Addition Postulate: Definition
The Segment Addition Postulate is a fundamental principle in geometry that states that if three points A, B, and C are collinear such that B lies somewhere on AC, then the sum of the lengths of the segments AB and BC is equal to the length of the entire segment AC.
Recommended Worksheets
Segment Addition Postulate: Formula
The formula for the segment addition postulate with respect to three collinear points A, B, C is given by
l(AB) + l(BC) = l(AC)
OR
AB + BC = AC
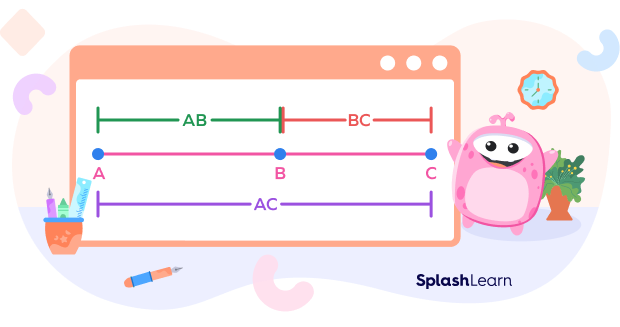
How to Use Segment Addition Postulate
Let’s understand the steps to use the segment addition postulate with the help of an example.
Example: Find the length of the line segment AB.
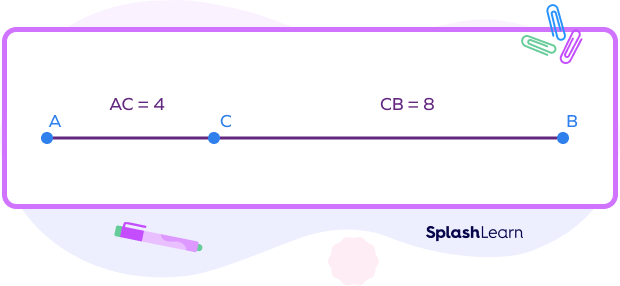
Step 1: Identify the collinear points and note down the given lengths of the line segments.
Here, C lies between A and B.
AC = 4
BC = 7
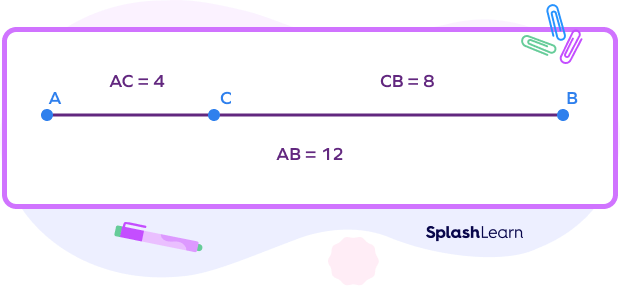
Step 2: Write the segment addition formula with respect to the given collinear points.
Here, AC + CB = AB
Step 3: Substitute the values and simplify.
AB = 4 + 8 = 12 units
How to Know if Three Points are Collinear
- If the point P lies between A and B, then AP + PB = AB.
- If AP + PB = AB, then P lies between A and B, and the points A, P, and B are collinear.
Facts about Segment Addition Postulate
- The segment addition postulate is not applicable to lines or rays.
- This postulate can identify the midpoint of the line segment. If AB + BC = AC and AB = BC, then B is the midpoint of AC.
Conclusion
In this article, we learned about the segment addition postulate, which is a fundamental property of line segments that helps us to identify collinear points. Let’s solve a few examples and MCQs for better understanding.
Solved Examples on Segment Addition Postulate
1. Does point B lie on segment AC if segment AB = 3 units, BC = 5 units, and AC = 6 units?
Solution:
AB = 3 units, BC = 5 units, and AC = 6 units
Let us calculate the sum of AB and BC.
l(AB) + l(BC) = 3 + 5 = 8 units
l(AC)=6 units
l(AB) + l(BC)$/neq$ l(AC)
Thus, B does not lie on the line segment AC.
2. In the given diagram, l(AC) = 28 units. Find x.

Solution:
B lies between the points A and C.
AB + BC = AC
2x + 3x + 3 = 28
5x + 3 = 28
5x = 25
x = 5
Thus, the value of x is 5.
3. The point R lies on the line segment PS, where PR = 5x, RS = (6x + 1) , and PS = 56 units. What will be the value of x, PR, RS and PS?
Solution:
As point S lies on the line segment PS, the equation will be:
PR+RS=PS
5x+6x+1=56
11x + 1 = 56
11x = 56 – 1
11x = 55
$x = \frac{55}{11}$
x =5
PR = 5$ \times$ 5 = 25 units
RS = 6(5) + 1=31 units
4. Find GH.
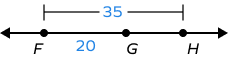
Solution:
G lies between F and H.
FH = 35 units
GF = 20 units
By segment addition postulate, FG + GH = FH
GH = FH – FG
GH = 35 – 20
GH = 15 units
Practice Problems on Segment Addition Postulate
Segment Addition Postulate: Definition, Formula, Examples, FAQs
What will be the value of ST if RS = 1 unit and RT = 13 units, and the point S lies on a line segment RT?
RS + ST = RT
1 + ST = 13
ST = 12
If the point Y bisects the line segment XZ, then
By the segment addition postulate, XY + YZ = XZ
Since Y is midpoint of XZ, we have XY = YZ
Thus, XZ = 2XY = 2YZ
The points IJKL are collinear: IJ = 9, JK = 11, and IL = 26. What is the length of KL?
IJ + JK + KL = IL
9 + 11 + KL = 26
KL = 6 units
What will be the value of x if Q lies on line segment PR such that PQ = 3x - 3, QR = 2x-1, and PR = 11?
$PQ + QR = PR$
$3x - 3 + 2x-1 = 11$
$5x = 11 + 4$
$x = 3$
Frequently Asked Questions about Segment Addition Postulate
How does the segment addition postulate differ from the angle addition postulate?
The Segment Addition Postulate deals with line segments and their lengths. The Angle Addition Postulate deals with the angles and their measures
Where is the segment addition postulate used in daily life?
It is used to find the measurement of walls, small objects with unknown parts of lengths and other similar items.
Can the Segment Addition Postulate be applied to non-collinear points?
No, the postulate specifically applies to collinear points. If the points are not on the same line, the postulate does not hold.
Which algebraic property is the segment addition postulate a part of?
The algebraic property of equality defines the segment addition of equality.
Is it possible to extend the segment addition postulate for more than three collinear points?
Yes, the postulate can be extended to include more than three collinear points. The sum of the lengths of the intermediate line segments would be equal to the length of the entire line segment.
AB + BC + CD = AD





































