What Is the Hypotenuse Leg Theorem?
Hypotenuse Leg Theorem (HL theorem) is used to prove the congruence of two right angled triangles. It is also known as the RHS (Right angle-Hypotenuse-Side) congruence rule.
In a right triangle, there is one right angle ($90^{\circ}$ angle) and two acute angles. The side opposite to the right angle is called hypotenuse. It is the longest side of the right triangle. The other two sides are called ‘legs’ of the right triangle.
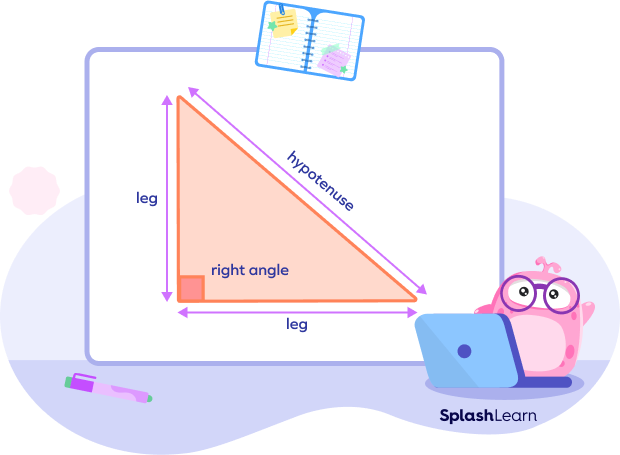
According to the HL theorem, if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of the other right triangle, then the two triangles are congruent.
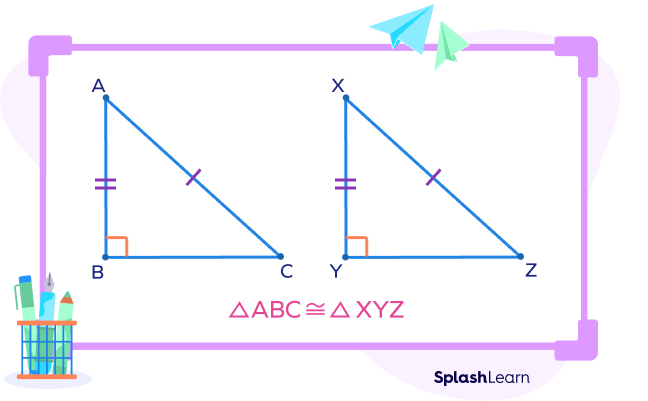
Hypotenuse Leg Theorem Statement
HL triangle congruence theorem: If the hypotenuse and one leg of one right triangle are congruent to the hypotenuse and leg of the other right triangle, then the two right triangles are said to be congruent.
In other words, two right triangles are congruent if the corresponding lengths of the hypotenuse and one leg are equal.
Hypotenuse Leg Theorem Proof
Given: In right triangles △ABC ≅△XYZ, AB = XY and AC = XZ
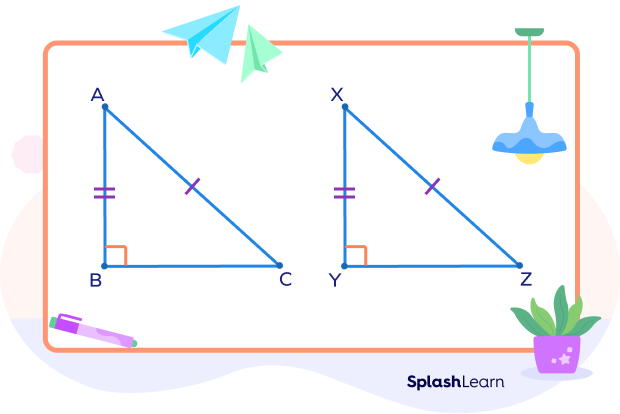
To prove: △ABC ≅△XYZ
Proof:
| Statement | Reason |
|---|---|
| AB2 + BC2 = AC2 | Pythagoras theorem |
| XY2 + YZ2 = XZ2 | Pythagoras theorem |
| XZ = AC …(1) | Given |
| AB2 + BC2 = XY2 + YZ2 …(2) | From (1) |
| AB = XY …(3) | Given |
| XY2 + BC2 = XY2 + YZ2 | From (2) and (3) |
| BC2 = YZ2 | Canceling out XY2 |
| BC = XY | Taking positive square root |
| △ABC ≅△XYZ | By SSS criterion |
Facts about Hypotenuse Leg Theorem
- HL theorem (Hypotenuse Leg Theorem or Hypotenuse Leg Congruence Theorem) is also known as the RHS (Right angle-Hypotenuse-Side) congruence rule.
- The LA Theorem (Leg- Acute angle Theorem): If the leg and an acute angle of one right triangle are both congruent to the corresponding leg and acute angle of another right triangle, the two triangles are congruent.
Conclusion
In this article, we learned about HL theorem or HL congruence criterion to prove congruence of two right triangles. We learned the statement and also proved the theorem. Let’s use the HL theorem to solve a few examples and practice problems.
Solved Examples on HL Theorem (Hypotenuse Leg Theorem)
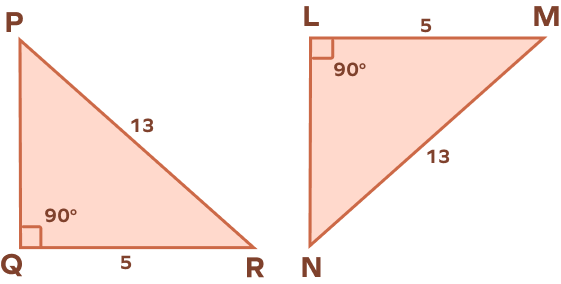
1. Is △PQR ≅ △NLM?
Solution:
To prove the congruence of right triangles, we will use the HL theorem.
In right triangles △PQR and △LMN, we have
∠Q = ∠L = 90°
PR = MN = 13 units
QR = LM = 5 units
By HL Theorem, one leg and hypotenuse of △PQR are congruent to one leg and hypotenuse of △LMN.
Thus, △PQR ≅ △NLM
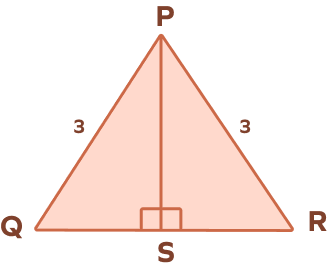
2. In the △PQR, if PS is the perpendicular bisector of the side QR, then prove that ∠QPS = ∠RPS.
Solution:
In △PQR, PS is the perpendicular bisector of QR.
$\Rightarrow$ QS = SR …(1)
In △PSQ and △PSR
∠PSQ = ∠PSR = 90°
PQ = PR = 3 units
QS = SR …from (1)
Thus, △PSQ ≅ △PSR …by HL Theorem
$\Rightarrow$ ∠QPS = ∠RPS …CPCTC (Corresponding parts of congruent triangles are congruent.)
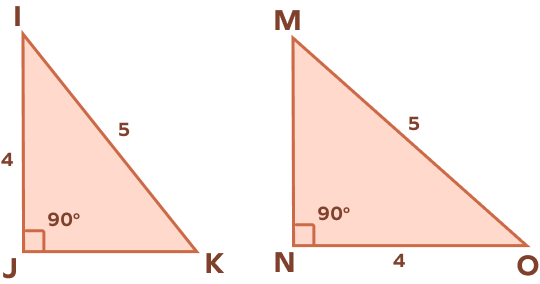
3. In the following figure, find the value of JK and MN.
Solution:
In △IJK and △ONM,
∠IJK = ∠ONM = 90°
IK = MO = 5 units
IJ = ON = 4 units
By HL Theorem,
△IJK ≅ △ONM
$\Rightarrow$KJ = MN (CPCTC)
KJ = MN = $\sqrt{5^{2}\;-\;4^{2}}$ (By Pythagoras theorem)
KJ = MN = $\sqrt{25 \;-\; 16}
KJ = MN = $\sqrt{9}$
KJ = MN = 3 units
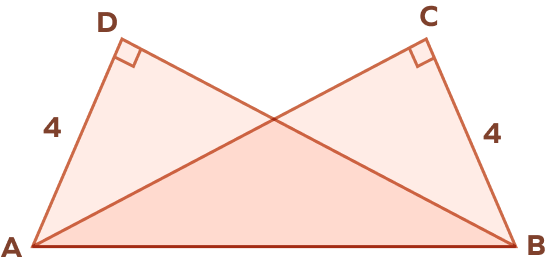
4. In the following figure, prove that △DAB ≅ △CBA.
Solution:
In △DAB and △CBA, we have
∠ADB = ∠ACB = 90°
AB = AB (common side)
AD = BC = 4 units
By HL Theorem,
△DAB ≅ △CBA
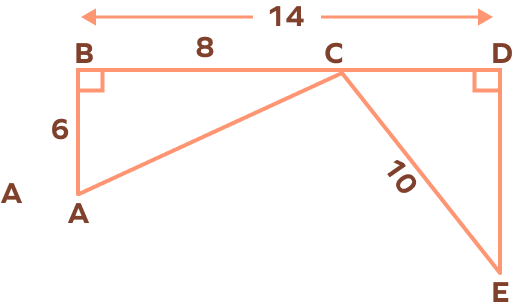
5. In the following figure, prove that △ABC ≅ △EDC.
Solution:
CD = BD – BC = 14 – 8 = 6 units
In △ABC, we have
$AC^{2} = AB^{2} + BC^{2}$
$AC^{2} = 6^{2} + 8^{2} = 36 + 64 = 100$
AC = 10 inches
In △ABC and △EDC,
∠ABC = ∠EDC = 90°
AC = CE = 10 units …hypotenuse
AB = CD = 6 units …leg
By HL Theorem,
△ABC ≅ △EDC
Practice Problems on HL Theorem (Hypotenuse Leg Theorem)
Hypotenuse Leg Theorem – Definition, Proof, Examples, FAQs
Which information is missing to prove △ABC ≅ △DEF by HL theorem?
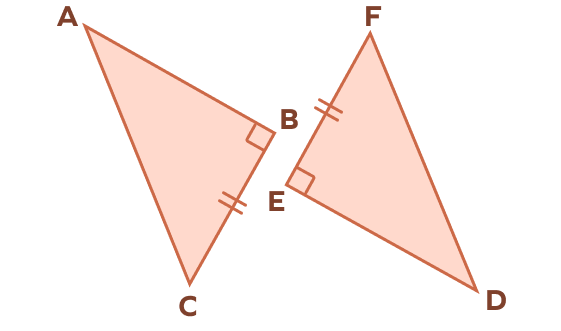
In the given right triangle, BC = EF are two congruent legs.
If the two hypotenuses are also equal, we can apply the HL theorem of congruence.
Missing information is AC = DF.
Which congruence theorem is used for proving △XYZ ≅ △UZY?
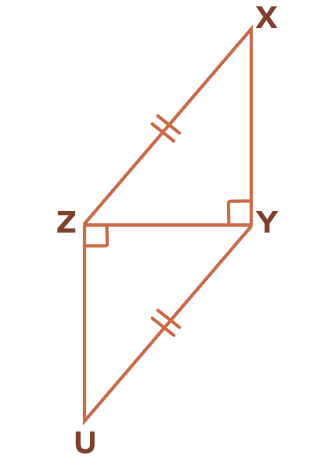
In △XYZ and △UZY
∠XYZ = ∠UZY = 90°
XZ = YU (given)
YZ = ZY (commons side)
By HL theorem,
△XYZ ≅ △UZY
Find the values of a and b that make △WXY ≅ △GFH
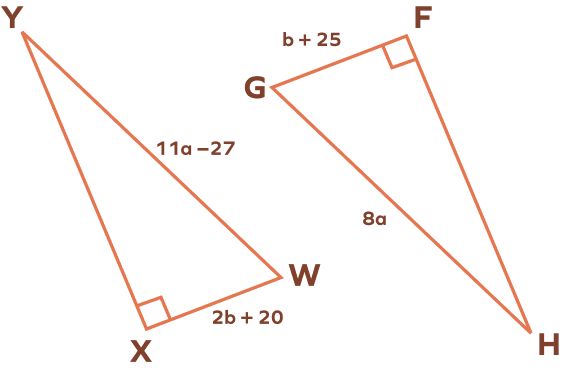
For △WXY ≅ △GFH, one leg should be congruent.
WX = GF
2b + 20 = b + 25
b = 5
Also, we need to have two congruent hypotenuses.
WY = GH
11a - 27 = 8a
3a = 27
a = 9
Frequently Asked Questions on HL Theorem (Hypotenuse Leg Theorem)
What is the Pythagorean Theorem?
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Hypotenuse² = Base² + Perpendicular².
What is the leg leg theorem (leg leg congruence)?
According to the leg-leg theorem, if the legs of one right triangle are congruent to the legs of another right triangle, then the triangles are said to be congruent.
What is the HL similarity theorem?
If the hypotenuse and one leg (H and L) of a right triangle is proportional to the hypotenuse and leg of the other right triangle, the triangles are said to be similar.
















