Like Fractions and Unlike Fractions: Definition, Examples, FAQs

What Are Like and Unlike Fractions?

If two or more fractions have the same denominator, they are called “like fractions.” For example, $\frac{2}{5},\frac{4}{5},\frac{1}{5},\frac{3}{5}$ are like fractions.

If two or more fractions have different denominators, they are called “unlike fractions.” For example, $\frac{2}{5},\frac{4}{3},\frac{1}{2},\frac{3}{7}$ are unlike fractions.

What Is a Fraction?

A fraction represents parts of a whole. A fraction has two parts. The number on the top of the line is called the numerator. It tells how many equal parts of the whole are taken.  The number below the line is called the denominator. It shows the total number of equal parts the whole is divided into or the total number of the same objects in a collection. 

Example 1: If a cake is divided into eight equal pieces, then each slice is “one-eighth” or “1 by 8” or $\frac{1}{8}$ of the whole. 

Example 2: There are a total of 5 children. 3 out of 5 are girls. So, the fraction of girls is 35.

What Are Like Fractions?

Like Fractions Definition: Like Fractions are the fractions that have the same denominator. Like fractions are fractions whose denominators are equal. 

In other words, in the like fractions, the number of equal parts the whole is divided into remains the same, which is represented by the common denominators.

Like Fractions Examples: In $\frac{3}{12},\frac{4}{12},\frac{11}{2}$, the denominator of each of the fractions is the same, 12. So, they are like fractions.

What Are Unlike Fractions?

Unlike Fractions Definition: Unlike Fractions are the fractions which have different denominators. Their denominators are not equal. 

So, how do you identify unlike fractions? Simply check their denominators!

Unlike Fractions Examples: In $\frac{3}{7},\frac{2}{5},\frac{3}{8}$, the denominator of each of the fractions is not the same so, they are like fractions. In other words, in unlike fractions, the number of equal parts the whole is divided into are different.

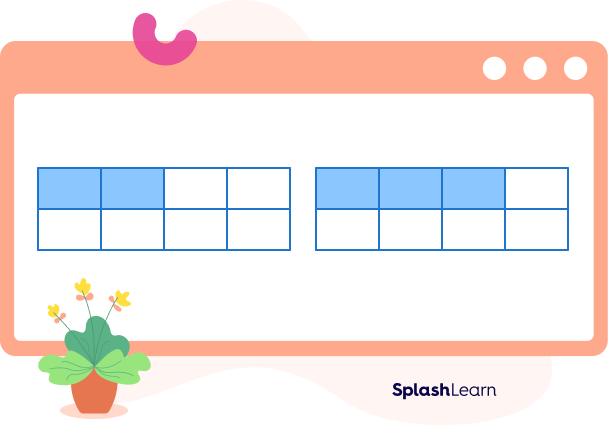
Comparing Like and Unlike Fractions

We can compare the fractions using different ways. To compare like fractions, simply compare their numerators.

Example: Let us compare like fractions $\frac{2}{8}$ and $\frac{3}{8}$. 

To compare like fractions, simply compare their numerators. 

$2<3$

Thus, $28<38$. 

Here’s another way.

To represent $\frac{2}{8},2$ parts are shaded out of 8 equal parts. 

To represent $\frac{3}{8},3$ parts are shaded out of 8 equal parts.

The shaded region for $\frac{2}{8}$ is less than the shaded region for $\frac{3}{8}$.

Thus, $\frac{2}{8}<\frac{3}{8}$.

Comparing like fractions is easy as we just have to compare their numerators, but for comparing unlike fractions, we have to convert unlike fractions to like fractions. 

While comparing two or more unlike fractions, there are two different cases. 

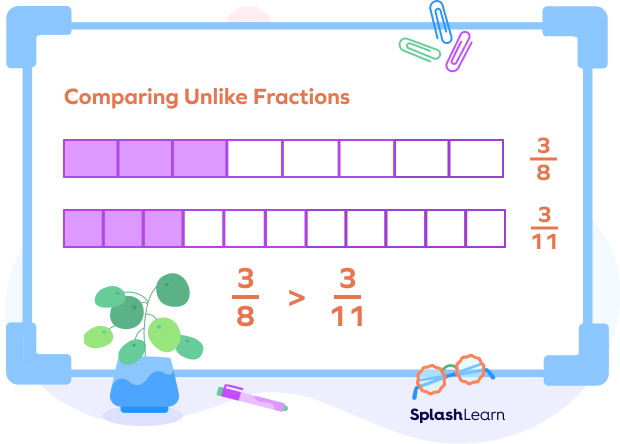
• Unlike Fractions with Same Numerators

In this case, the fraction with the greater denominator is the smallest and the fraction with a smaller denominator is the largest. 

Suppose we have to compare $\frac{3}{8}$ and $\frac{3}{11}$. 

Numerators are the same. $\frac{3}{11}$ has the greater denominator. 

Thus, $\frac{3}{11}<\frac{3}{8}$.

Since 3 shaded parts of 8 are bigger than the 3 shaded parts of 11, we can say that $\frac{3}{8}>\frac{3}{11}$. 

• Unlike Fractions with Different Numerators

In this case, we can use two methods:

1. Cross multiplication

To cross multiply fractions, we multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction. Finally compare the products to compare the fractions.

(Note that you can use this method to compare any two fractions, but it is convenient to use when comparing unlike fractions.)

Example:  $\frac{3}{7}$ and $\frac{1}{3}$

Cross multiplying, we get

$3\times 3>1\times 7$

$9>7$

Thus, $\frac{3}{7}>\frac{1}{3}$

2. Making Denominators Same (LCM method)

We first convert unlike fractions to like fractions by taking LCM of their denominators. Suppose we have to compare $\frac{3}{4}$ and $\frac{2}{5}$. The LCM of the denominators 4 and 5 is 20. 

$\frac{3\times 5}{4\times 5}=\frac{15}{20}$ and $\frac{2\times 4}{5\times 4}=\frac{8}{20}$

Here, $15>8$

$\frac{15}{20}>\frac{8}{20}$

So, $\frac{3}{4}>\frac{2}{5}$

Addition of Like and Unlike Fractions

We can simply add two or more like fractions by adding the numerators and keeping the denominators the same. 

Example: $\frac{2}{5}+\frac{8}{5}$

$\frac{2}{5}+\frac{8}{5}=\frac{2+8}{5}=\frac{10}{5}=2$

For adding two unlike fractions, we first convert them to like fractions by finding the LCM of the denominators and then adding them.

Example: $\frac{1}{5}+\frac{3}{7}$ 

LCM of 5 and 7 = 35

$\frac{1\times 7}{5\times 7}=\frac{7}{35}$ and $\frac{3\times 5}{7\times 5}=\frac{15}{35}$

$\frac{1}{5}+\frac{3}{7}=\frac{7}{35}+\frac{15}{35}=\frac{22}{35}$

Subtraction of Like Fractions and Unlike Fractions

We can simply subtract two or more like fractions by subtracting the numerators and keeping the denominators the same. 

Example: $\frac{8}{5}–\frac{2}{5}$

$\frac{8}{5}–\frac{2}{5}=\frac{8–2}{5}=\frac{6}{5}$

For subtracting two unlike fractions, we first convert them to like fractions by finding the LCM of the denominators and then subtract them.

Example: Subtract $\frac{1}{5}$ from $\frac{3}{7}$. 

LCM of 5 and 7 = 35

$\frac{1\times 7}{5\times 7}=\frac{7}{35}$ and $\frac{3\times 5}{7\times 5}=\frac{15}{35}$

$\frac{3}{7}–\frac{1}{5}=\frac{15}{35}–\frac{7}{35}=\frac{8}{35}$

Multiplication of Like and Unlike Fractions

For multiplying any two fractions (like or unlike fractions), we multiply the numerators separately and multiply the denominators separately, and then convert into the lowest term if needed. 

Example 1: $\frac{3}{5}\times \frac{2}{5}=\frac{3\times 2}{5\times 5}=\frac{6}{25}$

Example 2: $\frac{1}{7}\times \frac{14}{15}=\frac{1\times 14}{7\times 15}=\frac{2}{15}$

Division of Like Fractions and Unlike Fractions

To divide a fraction by another fraction, we multiply the first fraction by the reciprocal of the second fraction. 

Example 1: $\frac{3}{5}÷\frac{2}{5}=\frac{3}{5}\times \frac{5}{2}=\frac{3}{2}$

Example 2:  $\frac{5}{7}÷\frac{25}{14}=\frac{5}{7}\times \frac{14}{25}=\frac{2}{5}$

Conclusion

In this article, we learned about like and unlike fractions, their definitions, arithmetic operations on them, and how to compare them. Understanding the difference between these fractions is essential since we use these concepts in many higher grade topics. Let’s solidify our understanding by practicing examples and MCQs.

Solved Examples on Like and Unlike Fractions

1. Kim had $\frac{3}{8}$ of a pizza and Sherry had $\frac{4}{8}$ of the pizza. What fraction of the pizza did they have altogether?

Solution: Fraction of pizza that Kim ate $=\frac{3}{8}$

Fraction of pizza that Sherry ate $=\frac{3}{8}$

Fraction of pizza they had altogether $=\frac{3}{8}+\frac{4}{8}=\frac{3+4}{8}=78$

2. Compare $\frac{7}{18}$ and $\frac{5}{21}.

Solution: Using cross multiplication, we get

$7\times 21=147$

$5\times 18=90$

$147>90$

So, $\frac{7}{18}>\frac{5}{21}$. 

3. Multiply $\frac{5}{19}$ and $\frac{38}{35}$. 

Solution: 

$\frac{5}{19}\times \frac{38}{35}=\frac{5\times 38}{19\times 35}=\frac{2}{7}$

4. Divide the sum of $\frac{1}{7}$ and $\frac{4}{9}$ by $\frac{37}{21}$. 

Solution:

Let’s find $\frac{1}{7}+\frac{4}{9}$.

LCM of 7 and 9 = 63

$\frac{1\times 9}{7\times 9}=\frac{9}{63}$

$\frac{4\times 7}{9\times 7}=\frac{28}{63}$

$\frac{1}{7}+\frac{4}{9}=\frac{9}{63}+\frac{28}{63}=\frac{37}{63}$

$\frac{37}{63}÷\frac{37}{21}=\frac{37}{63}\times \frac{21}{27}=\frac{1}{3}$

5. Subtract $\frac{2}{9}$ from $\frac{4}{15}$. 

Solution: 

Let’s find $\frac{4}{15}–\frac{2}{9}$.

LCM of 15 and 9 = 45

$\frac{4\times 3}{15\times 3}=\frac{12}{45}$ and $\frac{2\times 5}{9\times 5}=\frac{10}{45}$

$\frac{4}{15}–\frac{2}{9}=\frac{12}{45}–\frac{10}{45}=\frac{2}{45}$

Practice Problems on Like and Unlike Fractions

Frequently Asked Questions on Like and Unlike Fractions