Absolute Value – Definition, Function, Symbol, Examples, Facts, FAQs

What Is the Absolute Value of a Number?

The absolute value of a number tells us how far a given number is from the origin on a number line. 

The absolute value only talks about distance, and not direction. We know that distance is a non-negative quantity. Thus, the absolute value of a number can never be negative.

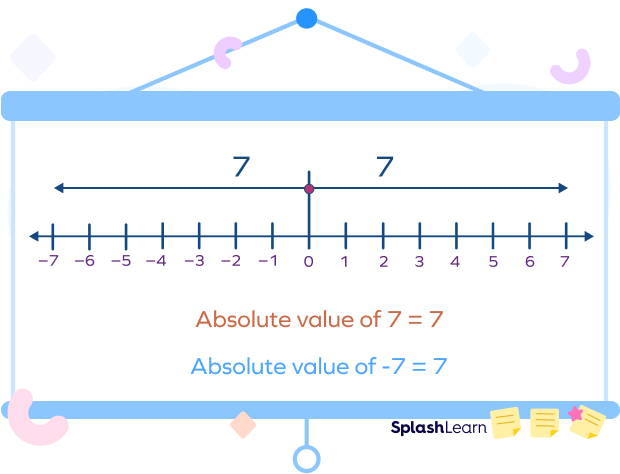
So, what does absolute value mean? Observe the diagram. Here, we can see that

7 is 7 units to the right of 0.

Thus, the absolute value of 7 is 7.

-7 is 7 units to the left of 0.

Thus, the absolute value of -7 is 7.

Absolute Value: Definition

Absolute value of a number can be defined as the distance of the number from the origin on a number line.

Absolute Value: Symbol

Absolute value of a number is represented by writing the number between two vertical bars. Note that the vertical bars are not to be confused with parentheses or brackets. 

The absolute value of x is represented by |x|, and we read it as “absolute value of x.” It is also read as “modulus of x.” Sometimes, the absolute value of a number n is also written using the notion “abs(n).”

In the previous example, we can write

 $|7| = | \;–\; 7| = 7$

How to Find the Absolute Value of a Number

The absolute value of a positive number is the number itself. The absolute value of a negative number is written as the numeric value ignoring the negative sign. The absolute value of 0 is 0.

Absolute Value of 0

The distance of the point zero from zero is 0 itself. Thus, the absolute value of 0 is 0.

Absolute Value Properties

Non negativity: Absolute value of a number is always non-negative.

$ | n | \ge 0$

Symmetry: The absolute value of a number equals the absolute value of its additive inverse. 

$| \;-\; x | = | x |$

Positive definiteness: Absolute value of a number is 0 only if the number is 0.

$| n | = 0$ if and only if $n = 0$

On the same lines, we can say that $| x \;–\; y | = 0 ↔ x = y$

Multiplicativity: The absolute value of the product of two numbers is the product of the absolute values of the individual numbers.

$|x\times y| = | \times | \times | y |$

Preservation of division (equivalent to multiplicativity): 

$|\frac{x}{y}| = |\frac{x}{y}| …y \neq 0$

Sub-additivity: The absolute value of the sum of two numbers is less than or equal to the addition of the absolute values of the individual numbers.

$|x + y| \le | x | + | y |$

Equivalent to sub-additivity: $| x \;–\; y | \ge | | x | \;–\; | y | |$

Triangle inequality (equivalent to subadditivity): $| x \;–\; y | \le | x \;–\; z | + | z \;–\; x |$

Idempotence: The absolute value of an absolute value of a number is simply the absolute value.

$| | x | | = | x |$

Absolute Value Inequalities

Let’s discuss two important absolute value inequalities.

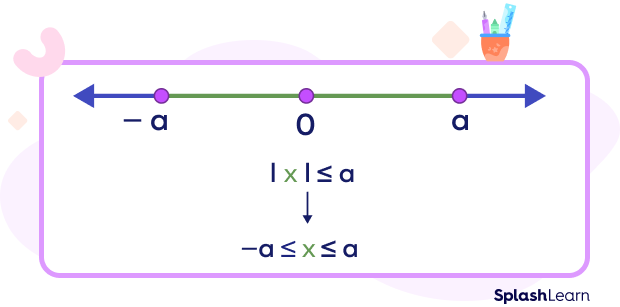
1. $| x | \le a  ⇔ \;−\; a \le x \le a$

This is often referred to as AND inequality.

Example: $|x \;−\; 5| \le 7 ⇔ \;−\;7 \le x \;−\; 5 \le 7$

      $⇔ \;−\; 2 \le x \le 12$

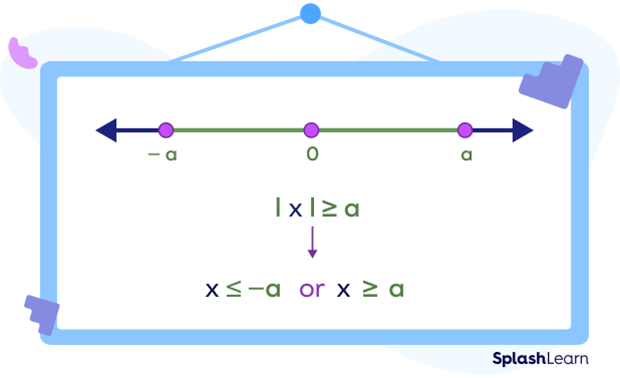
2. $| x | \ge a ⇔ x \le \;−\; a\; or\; x \ge a$

This is often referred to as OR inequality.

Example: $| x | \ge 3 ⇔ x \le \;−\;3$ or $x \ge 3$

Absolute Value of Real Numbers

The absolute value of a positive real number is the number itself. The absolute value of a negative real number is the number without a negative sign. The absolute value of 0 is 0.

Thus, for a real number x, the absolute value is given by: 

$| x | = x$ if $x \ge 0$

$| x | = \;–\; x$ if $x \lt 0$

Absolute Value on a Number Line

As mentioned earlier, the absolute value of a number tells us the distance of a number from zero on a number line. 

It is easy to understand the absolute value of integers (or any number) using the number line.

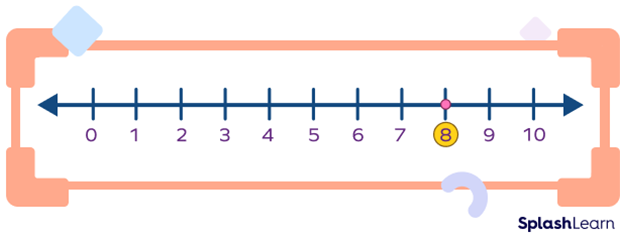
Example: The absolute value of 8 is 8.

$| 8 | = 8$.

Note that the absolute value of $\;–\; 8$ is also 8. 

$| \;–\; 8 | = 8$.

Absolute Value of a Number Examples

• $| 1 | = 1$
• $| \;-\;1| = 1$
• $| 3.5 | = 3.5$
• $| 0 | = 0$
• $| 7.9 | = 7.9$
• $| 5 \;–\; 3 | = | 2 | = 2$
• $| \;–\; 1 + 6 | = | 5 | = 5$
• $| \;–\; 6 \times 2| = | \;–\; 12 | = 12$

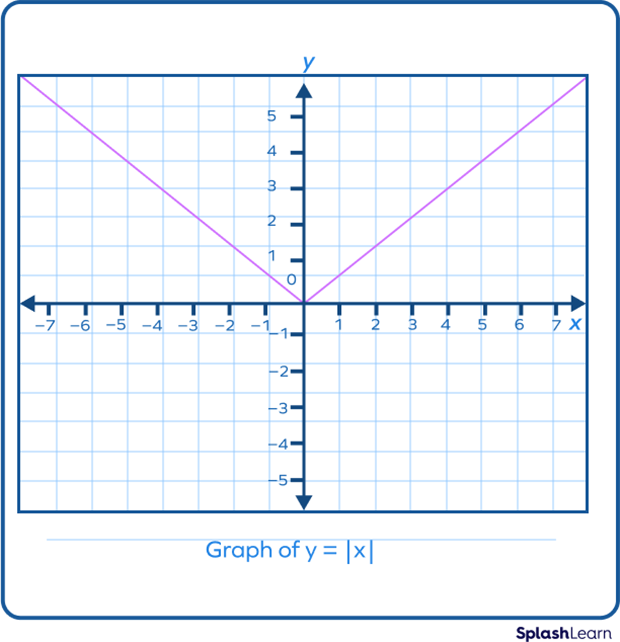
Absolute Value Function

The absolute value function can be given by f(x) = |x| such that:  

• $| x | = + x$  for $x \gt 0$
• $| x | = \;–\; x$  for  $x \lt 0$

Applications of Absolute Value

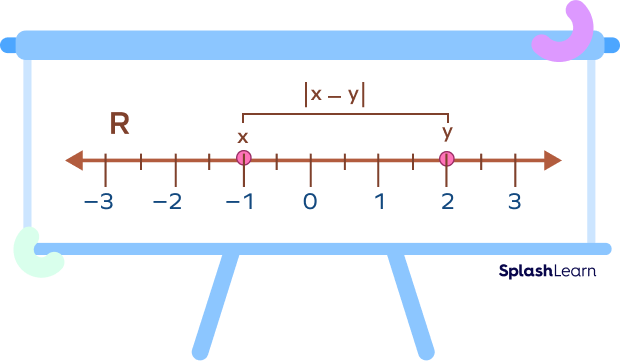
• To find the distance between two points.

The absolute value of the difference of two real numbers (absolute difference) is the distance between them.

• To identify and remove outliers in data analysis.
• To set tolerance in quality analysis.
• To determine the degree of variation in the data compared from a certain point.

Facts about Absolute Value

Conclusion

In this article, we learned about the absolute value of a number, its symbol, properties, absolute value function, and we also learned its applications. Let’s move ahead and solve a few examples and MCQs based on the concept of absolute value for practice.

Solved Examples on Absolute Value

1. What is the absolute value of  $\;–\;18$?

Solution: 

The absolute value of a negative number is written as the numeric value, ignoring the negative sign. 

The absolute value of $\;-\;18 = |\;-\;18| = 18$

2. Find the value of $-|\frac{\;-\;15}{22}|$.

Solution: 

First, focus on the absolute value part.

The absolute value of $\;-\;\frac{15}{22} = |\frac{-15}{22}| = |\frac{15}{22}|$

There’s a minus sign outside the absolute value. It will get tagged along with the answer.

$-|\frac{-15}{22}| = \frac{-15}{22}$

3. Find: $|-9| + |10|$.

Solution:

Here, 

|\;-\; 9 = 9|

$|10| = 10$

Thus, $|\;-\;9| + |10| = 9 + 10 = 19$

4. Find the absolute value.

$|5|, |\;-\;11|, |0|, |\;-\;7|, |\;-\;10|$

Solution: 

$|5| = 5$

$|\;-\;11| = 11$

$|0| = 0$

$|\;-\;7| = 7$

$|\;-\;10| = 10$

5. Simplify: $|x \;−\; 1| \le 2$

Solution:

$|x \;−\; 1| \le 2$

$\;−\;2 \le x \;−\; 1 \le 2$

$(\;−\;2 + 1) \le  x  \le (2 + 1)$

$\;−\; 1 \le  x  \le 3$

Practice Problems on Absolute Value

Frequently Asked Questions about Absolute Value