What is the column method?
When we arrange the numbers or shapes or objects one above the other, we refer to it as column method. In other words, the column method is a mathematical way of performing a calculation where the numbers to be added or subtracted or multiplied are set out above one another in columns.
For example:

We use the column method for three basic operations i.e.addition, subtraction and multiplication.
Recommended Games
Addition and Subtraction Column Method
Column method of addition and subtraction is the method in which the numbers are ‘carried’ and ‘borrowed’. It is set out like this: The calculation during addition and subtraction is done by ‘carrying’ and ‘borrowing’ numbers from column to column.
Recommended Worksheets
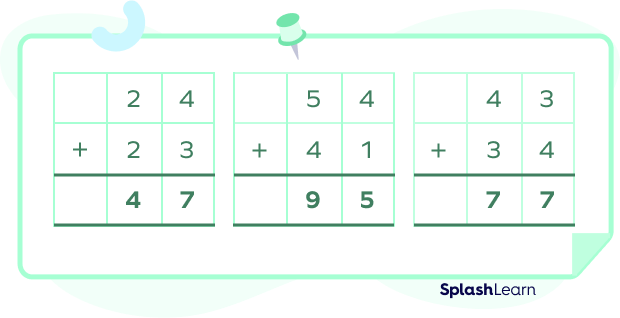
Column Method Addition
The column method of addition is also known as columnar addition. Column addition is a formal method of adding two or more numbers.
For example:
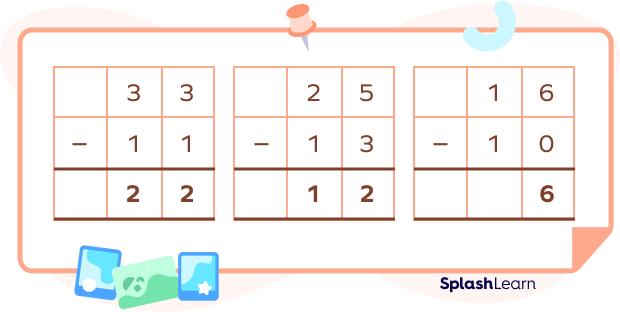
What is Column Subtraction?
The column subtraction is a way of finding the difference between two or more numbers by arranging them one above the other .
Column method Subtraction:
Why is Place Value Important in the Column Method?
The column method is the quickest way to add and subtract, but place value plays an important role in the column method.
Let’s look at the example below and use column addition.
- First, the numbers are lined up one above the other.
- Secondly, we add the ones and write the answer.
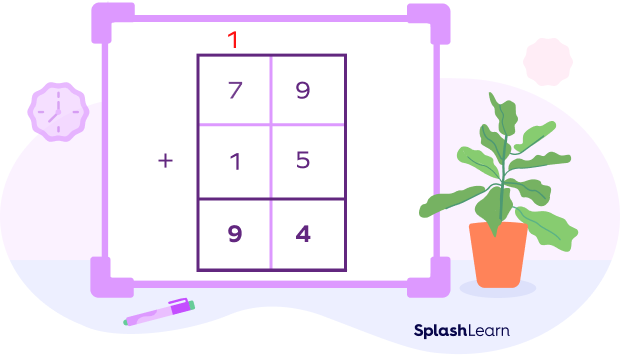
For example: Adding $9$ and $5$ gives an answer of $14$, but we write only the ones under the line – in this case, it’s the digit $4$.
- The third step is to regroup the tens under the tens column. In $14$, the digit $1$ is the value of the tens.
- Add the digits at the tens place. In our example, $8 + 1 = 9$, but we add 1 from under the line. So the answer for the tens is $9$.
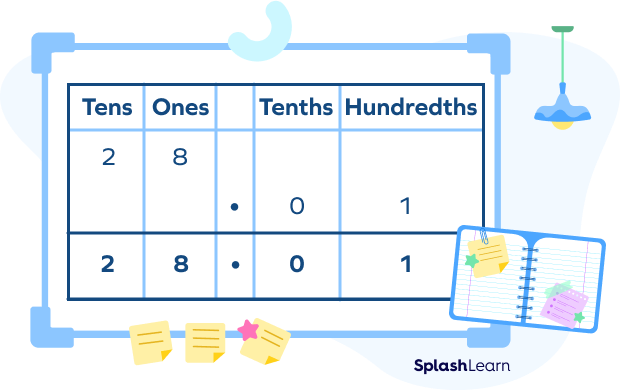
- When two numbers of different digits are added we can place them correctly using place value. For example: the decimal number $0.1$ and a number $28$.
The Expanded Column Method
The expanded method is the breaking down each of the numbers in your sum into the smaller, more manageable numbers that they are made up of. We basically break down the numbers in the expanded form.
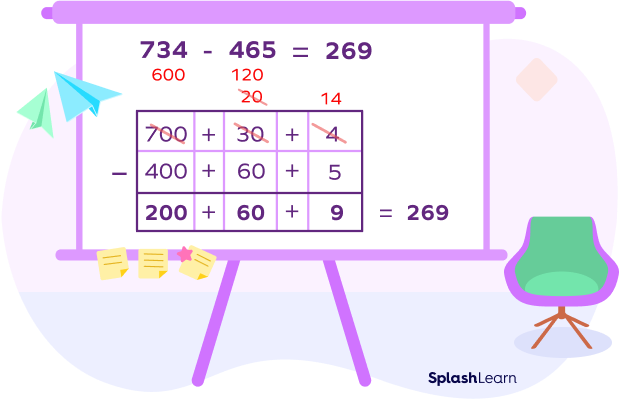
For example, the number $782$ can be broken down into: $700 + 80 + 2$
The expanded method is an addition sum is carried out in the following way:
Suppose, we have to add $47 + 134$
Firstly, we will expand $47 and 134$.
$47 = 40 and 7 and 134 = 100, 30 and 4$
Now we sort the numbers into hundreds, tens, and ones and add them in their groups.
- We will add the digits at ones place.
In this example, we add $7 + 4 = 11$. We keep 1 at the ones place and take another $1$ to the tens place.
- We will add the digits at tens place.
In this example, we add $30 + 40 + 10 = 80$
- We will add the digits at the hundreds place.
In this example, we add $100 + 0 = 200$
Now, we add all of our digits together, we get $100 + 80 + 1 = 181$
Another example is given below:

Let us take an example of an expanded column method of subtraction.
The Column Method for Subtraction without Borrowing
Sometimes we don’t have to borrow the digits from a column in subtraction.
For example: $76 – 42$
The first step is to sort your numbers into tens and ones:
Tens $→ 7 and 6$
Ones $→ 4 and 2$
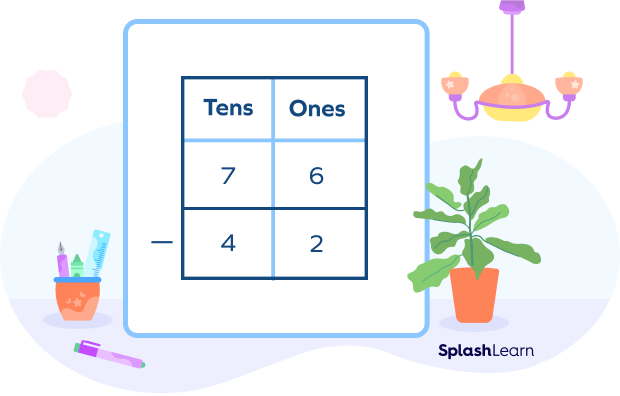
We should always place the biggest numbers in the top row of the columns.
Now you can subtract the numbers in each column:
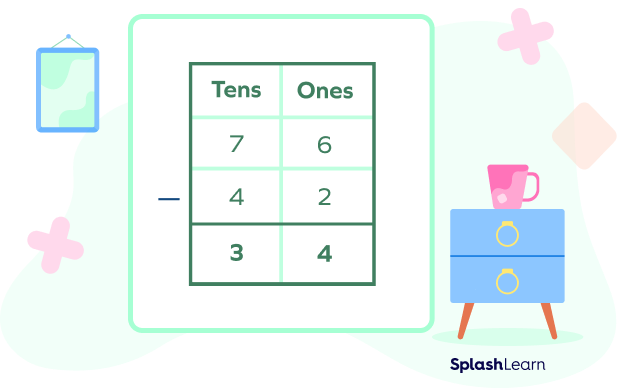
The answer to the sum is $76 – 42$ is $34$.
The Column Method for Addition without Borrowing
We use the column method for addition without borrowing or carrying any values between columns.
For example: $282 + 615$
On expanding, we get
Hundreds $→ 200$ and $600$
Tens $→ 80$ and $10$
Ones$→ 2$ and $5$
Now, put the values into their columns:
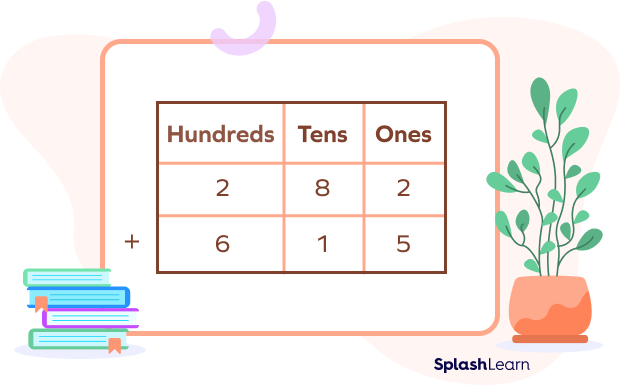
Next, we add up all of your values within their groups.
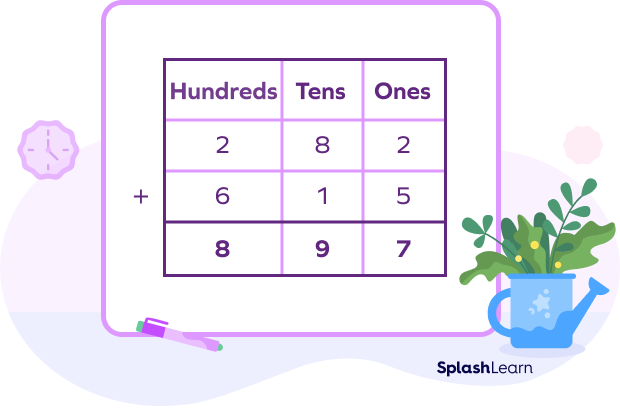
Therefore, the answer to the sum $262 + 615$ is $897$.
The Column Method of Multiplication
We also use the column method to multiply two numbers which involves writing one number underneath the other in a similar way to column addition and subtraction.
When we multiply two numbers using the column method multiplication, we use the following steps:
Suppose we are multiplying $96$ and $36$.
Step I: We multiply the multiplicand $(96)$ by the ones digit of multiplier $(6)$ i.e.,
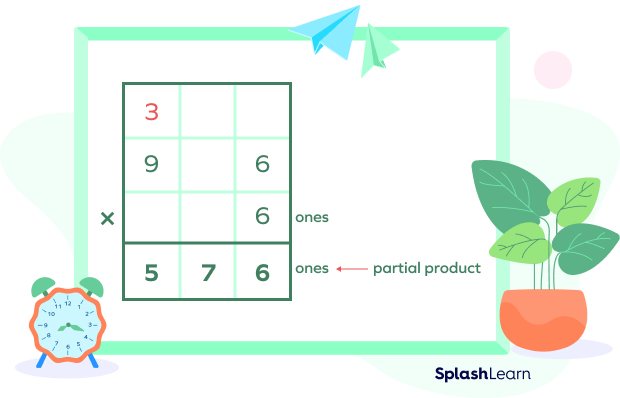
Step II: The next step is to multiply the multiplicand $(96)$ by the tens digit of multiplier $(3)$ i.e.,
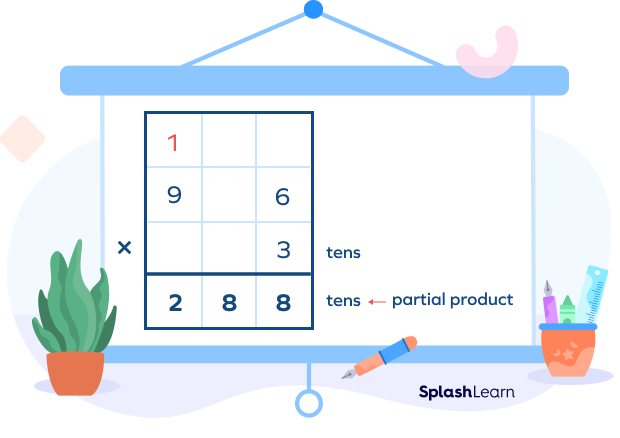
Step III: The next step is to add the partial products i.e.,
Partial product $1 (576 ones) +$ Partial product $2 (288 tens)$
$576 × 1 + 288 × 10$
$576 + 2880 = 3456$
It actually means:
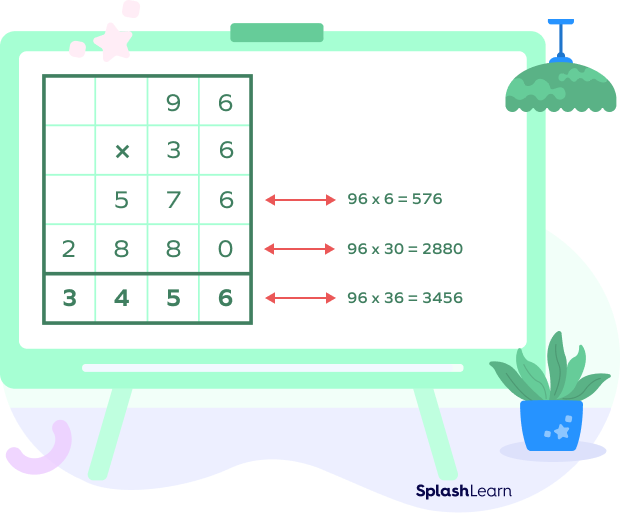
Now we shall apply the same method for multiplying a $3-$digit number by a $2-$digit number.
Example:
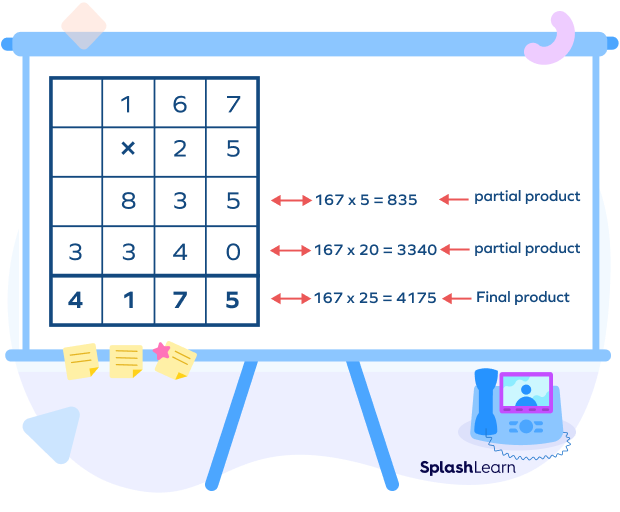
Let’s take another example. Find the product of $145$ times $12$ using the column method.
Step I:
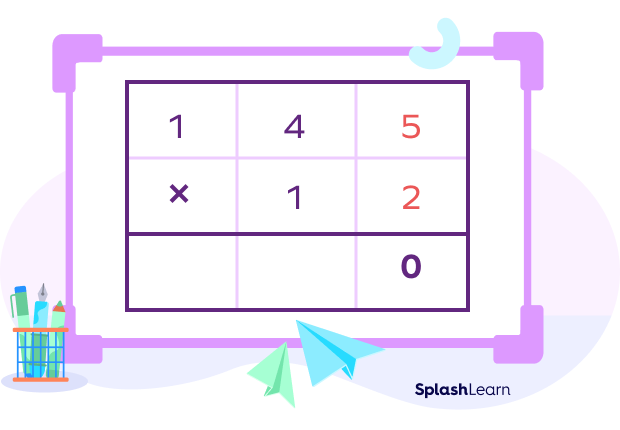
Step II:-
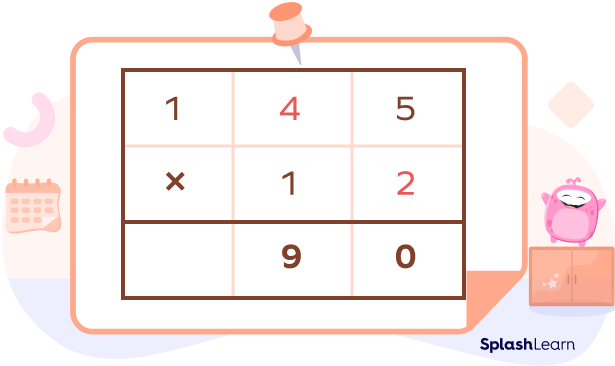
Step III:
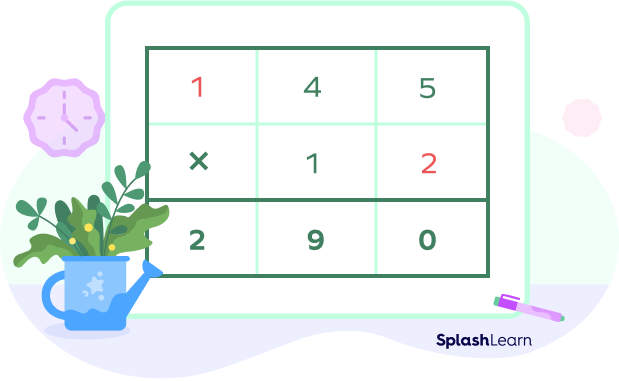
Step IV:
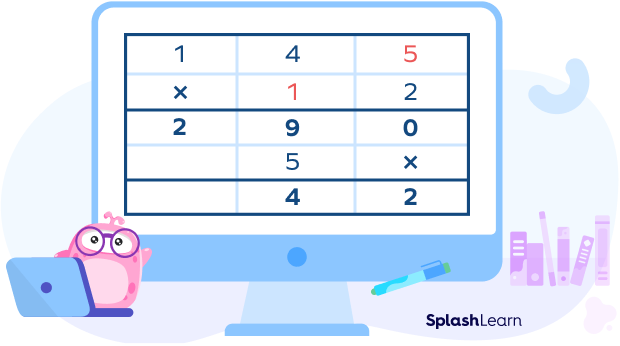
Step V:
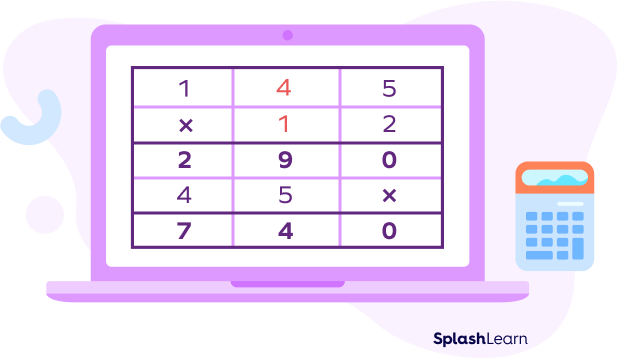
Step VI:
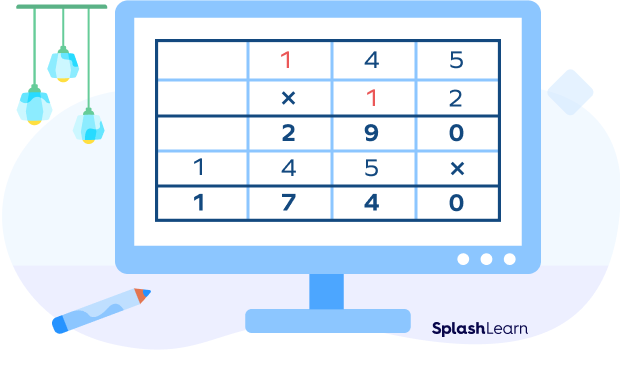
Solved Examples
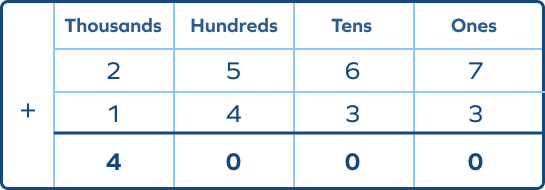
1. Find the error in the following.
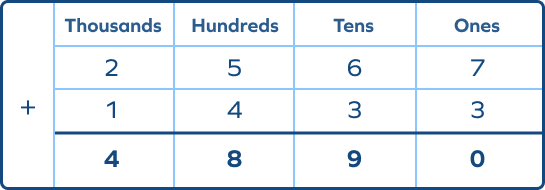
Answer: The error is that the tens and hundreds columns aren’t correctly added. The carryover digits weren’t added. The correct sum will be:
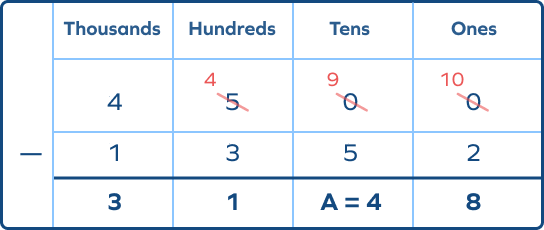
2. Find the value of ‘A’ in the following.
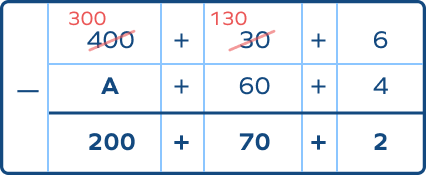
Solution: $300 – $A$ = 200$
$So, $A$ = 100$
3. The cost of 1 necklace is Rs $342$. What will be the cost of $23$ necklaces? If Sharon has Rs $8000$, how much money will be left after paying for the necklaces?
Answer: Cost of 1 necklace $=$ Rs $342$
Cost of $23$ necklaces $= 342 ✕ 23 =$ Rs $7866$
Cost of $23$ necklaces $= 6000 + 900 + 800 + 120 + 40 + 6 =$ Rs $7866$
Amount left $= 8000 – 7866$
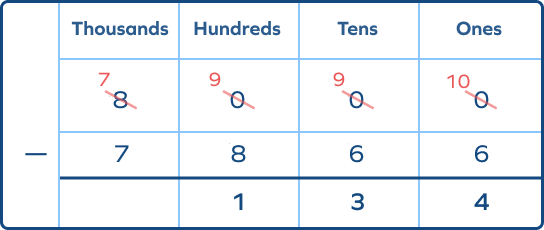
Amount left $=$ Rs $134$
Practice Problems
Column Method - Definition With Examples
If we use the column method to multiply 543 and 16, then what will come in one's place?
$6\times3 = 18$, so at ones place, we will get $8$.
What will replace A in the following?
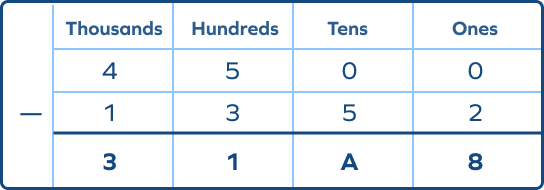
$4500 − 1352 = 3148$
So, at tens place, we get 4.
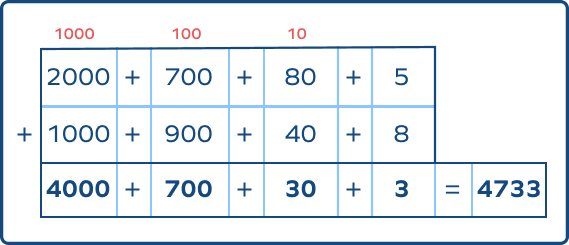
Add: 2785 and 1948
$2785 + 1948 = 4733$
Frequently Asked Questions
What is the difference between the column method and horizontal method?
The column method is the method of arranging the numbers one above the other and adding, subtracting or multiplying in the columns. On the other hand, the horizontal method is the way of arranging the numbers in a horizontal line then the terms are arranged to collect all the groups of like terms.
What is another name for the column method of addition?
The other name for column method of addition is columnar addition or vertical method of addition.
What is the column method division?
The column method division is a simple way of the traditional long division method. The lines are drawn in order to separate the digits of the divisor. Each place-value column is solved from left to right.































