What Are Prime Numbers?
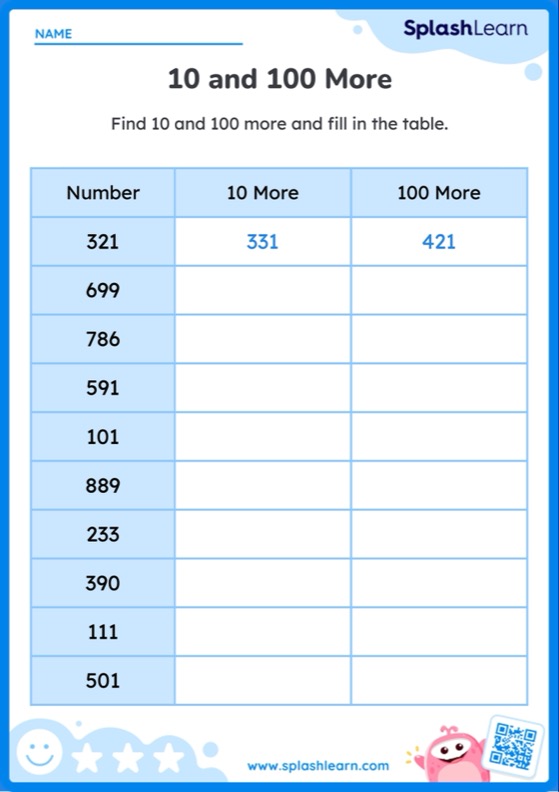
Prime numbers are numbers greater than 1. They only have two factors, 1 and the number itself. This means these numbers cannot be divided by any number other than 1 and the number itself without leaving a remainder.
Numbers that have more than 2 factors are known as composite numbers.
Examples and Non-examples of Prime Numbers
Difference Between Prime Number and Composite Number
The Sieve of Eratosthenes
In third century BCE, the Greek mathematician Eratosthenes found a very simple method of finding the prime numbers.
Follow the given steps to identify the prime numbers between 1 and 100.
Step 1: Make a hundred charts.
Step 2: Leave 1 as it is neither a prime number nor a composite number.
Step 3: Encircle 2 and cross out all its multiples as they are not prime.
Step 4: Encircle the next uncrossed number, which is 3, and cross out all its multiples. Ignore the previously crossed out numbers like 6, 12, 18, and so on.
Step 5: Continue the process of encircling the next uncrossed number and crossing out its multiples till all the numbers in the table are either encircled or crossed out, except 1.
So, from the table it is clear that 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 are the prime numbers.
There are 25 prime numbers between 1 and 100.
Terms Related to Prime Numbers
Co-Primes: Two numbers are said to be co-prime if they have only one common factor, that is, 1. It is not necessary for these numbers to be prime numbers. For example, 9 and 10 are co-primes. Let’s verify.
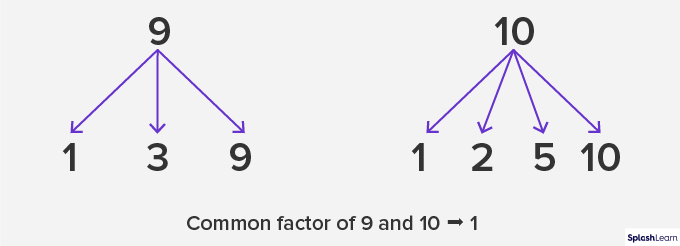
Note that pairs of any 2 prime numbers are always co-primes. This is because, out of their two factors, the common factor can only be 1. So, (3, 5), (11, 19) are some examples of co-primes.
Twin-Primes: A pair of prime numbers are known as twin primes if there is only one composite number between them. For example, (3, 5), (5, 7), (11, 13), (17, 19), etc.
List of Prime Numbers between 1 and 100
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
There are 25 prime numbers between 1 and 100.
List of Prime Numbers between 1 and 200
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
There are 46 prime numbers between 1 and 200.
List of Prime Numbers between 1 and 1,000
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
Some Facts about Prime Numbers
- 2 is the smallest prime number.
- 2 is the only prime number that is even.
- 2 and 3 are the only consecutive prime numbers.
- Except for 0 and 1, a whole number is either a prime number or a composite number.
- All odd numbers are not prime numbers. For example, 21, 39, etc.
- No prime number greater than 5 ends in a 5.
- Sieve of Eratosthenes is one of the earliest methods of finding prime numbers.
- Prime numbers get rarer as the number gets bigger.
- There is no largest prime number. The largest known prime number (as of September 2021) is $2^{82,589,933}$ − 1, a number that has 24,862,048 digits when written in base 10. By the time you read this, it may be even larger.
Solved Examples
Example 1: Classify the given numbers as prime numbers or composite numbers.
13, 48, 49, 23, 74, 80, 71, 59, 45, 47
Solution:
| Prime Numbers | Composite Numbers |
| 13, 23, 71, 59, 47 | 48, 49, 74, 80, 45 |
Example 2: Express 21 as the sum of two odd primes.
Solution:
21 = 19 + 2
Example 3: What prime numbers are there between 20 and 30?
Solution:
The prime numbers between 20 and 30 are 23 and 29.
Example 4: What is the greatest prime number between 80 and 90?
Solution:
The prime numbers between 80 and 90 are 83 and 89.
So, 89 is the greatest prime number between 80 and 90.
Practice Problems on Prime Numbers
Prime Numbers
Which of the following is not a prime number?
The factors of 81 are 1, 3, 9, 27, and 81. Rest of the numbers have only 2 factors— 1 and themselves.
What is the 10th prime number?
2, 3, 5, 7, 11, 13, 17, 19 and 23 are the first 9 prime numbers and 29 is the 10th prime number.
How many prime numbers between 40 and 50?
Prime numbers between 40 and 50 are 41, 43 and 47.
Which is the smallest odd prime number?
2 is the smallest even prime number. Next prime number is 3, so 3 is the smallest odd prime number.
Which of the following pairs of numbers are co-prime?
Co-prime numbers have only 1 as their common factor. Common factors of 7 and 14 are 1 and 7; Common factors of 15 and 27 are 1 and 3; Common factors of 25 and 35 are 1 and 5; Common factor of 8 and 55 is 1.
Frequently Asked Questions
Is one a prime number?
No, one is neither a prime number nor a composite number.
Can a prime number be negative?
No, prime numbers cannot be negative. Prime numbers belong to the set of natural numbers.
Why is 2 the only even prime number?
All even numbers larger than 2 are multiples of 2. So, 2 is the only even prime number.
What is the difference between a prime and a co-prime number?
A prime number has exactly two factors, 1 and the number itself. Co-prime numbers have only 1 as their common factor.
Which Is the largest known prime number?
The largest known prime number (as of September 2021) is 282,589,933 − 1, a number that has 24,862,048 digits. By the time you read this, it may be even larger than this.