What Are Alternate Exterior Angles?
When two lines (parallel lines) are cut by a transversal at two distinct lines, a pair of angles that are created on the alternate sides of a transversal and on the outer side (exterior side) of the two lines are called alternate exterior angles.
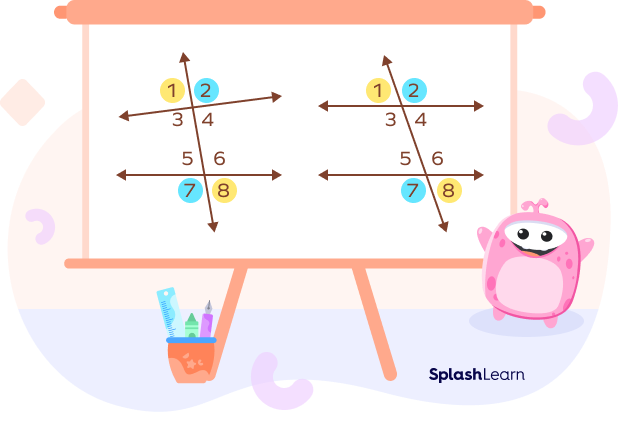
What do alternate exterior angles look like?
The diagram on the left side shows the alternate exterior angles formed by two non-parallel lines cut by transversal. The diagram on the right shows the alternate exterior angles formed by two parallel lines cut by transversal.
Recommended Games
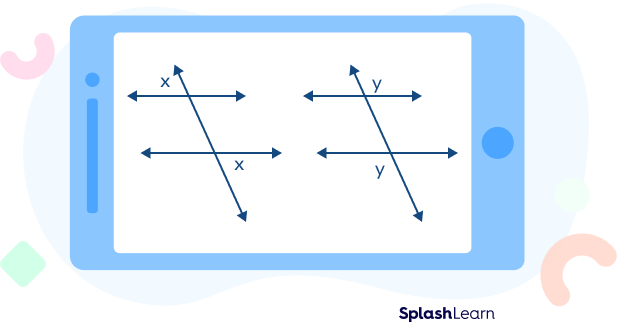
Alternate Exterior Angles: Definition
Definition of alternate exterior angles: A pair of angles formed on the alternate sides (opposite sides) of a transversal and on the exterior side of two lines cut by transversal are known as alternate exterior angles.
Recommended Worksheets
Alternate Exterior Angles Theorem
The alternate exterior angle theorem states that when two parallel lines are cut by a transversal, then the pair of alternate exterior angles formed are congruent.
Proof of Alternate Exterior Angles Theorem
Given: l || m and t is a transversal.
Alt tag: Parallel lines l and m cut by a transversal
To prove:
m∠1 = m∠8
m∠2 = m∠7
Proof:
| Statement | Reasoning |
|---|---|
| m∠1 = m∠4 | Vertically opposite angles |
| m∠4 = m∠8 | Corresponding angles formed by two parallel lines cut by a transversal are congruent. |
| m∠1 = m∠8 | by Transitive property |
Hence, proved.
Converse of Alternate Exterior Angles Theorem
The converse of alternate exterior angles theorem states that if the alternate exterior angles formed by two lines cut by a transversal are congruent, then the two lines are parallel to one another.
Facts about Alternate Exterior Angles
- Alternate exterior angles theorem is used to prove that two lines are parallel to each other.
- If the lines are not parallel, the alternate exterior angles are not congruent and do not have any relationship.
Conclusion
In this article, we learned about Alternate Exterior Angles. We discussed the definition, the alternate exterior angles theorem, converse, and the proof. Let’s solve a few examples and practice problems for better comprehension.
Solved Examples on Alternate Exterior Angles
Example 1: Find the value of x.
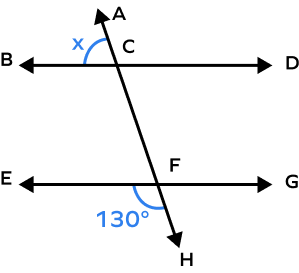
Solution:
m∠EFH = 130o
m∠ACB = x
Here, m∠EFH + m∠GFH = 180o …angles in a linear pair
Thus, 130 + m∠GFH = 180o
m∠GFH = 180o – 130o
m∠GFH = 50o
Now, m∠GFH = x …Alternate Exterior Angles Theorem
Thus, x = 50o
Example 2: If two alternate exterior angles formed by two lines and a transversal are (2x + 10) and (4x – 20), then what should the value of x be such that two lines are parallel?
Solution:
For two lines to be parallel, the alternate exterior angles should be equal to each other.
2x + 10 = 4x – 20
4x – 2x = 20 + 10
2x = 30
$x = \frac{30}{2}$
x = 15
Thus, the two lines will be parallel for x = 15.
Example 3: Find the value of y if the two parallel lines are cut by a transversal.
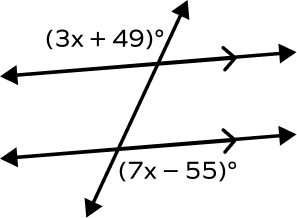
Solution:
The given angles (3y + 49) and (7y – 55) are alternate exterior angles.
By the alternate exterior angles theorem, we have
(3y + 49) = (7y – 55)
4y = 104
y=26
Practice Problems on Alternate Exterior Angles
Alternate Exterior Angles - Definition, Theorem, Examples, FAQs
Alternate exterior angles formed by two parallel lines cut by a transversal are
Alternate exterior angles are congruent when the two lines cut by a transversal are parallel.
Find m∠2.
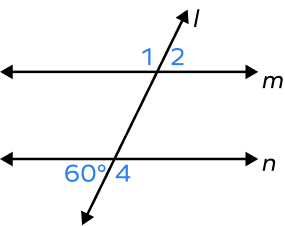
Alternate exterior angles formed by two parallel lines cut by a transversal are congruent.
The $60^{\circ}$ angle and ∠2 are alternate exterior angles formed by two parallel lines m and n cut by a transversal l are congruent.
Thus, m∠2 $= 60^{\circ}$
Alternate exterior angles lie on the ______of the transversal.
Alternate exterior angles lie on the opposite sides of the transversal.
Alternate exterior angles lie on the _____ of the parallel sides.
Alternate exterior angles lie on the outer side of the parallel sides.
Frequently Asked Questions about Alternate Exterior Angles
What are alternate interior angles?
Alternate interior angles are a pair of angles that are on opposite sides of a transversal line and inside the two intersected lines.
Is the alternate exterior angles theorem applicable when more than two parallel lines cut by a transversal?
Yes, we can extend the alternate exterior angles theorem to more than two parallel lines cut by a transversal.
Are alternate angles supplementary?
Alternate angles are not supplementary angles, but they will add up to 180 if the transversal is perpendicular to the parallel lines.
Are alternate exterior angles congruent?
Alternate exterior angles formed when two parallel lines are cut by a transversal are congruent.





























