What is the Angle Sum Property of a Triangle?
The “angle sum property of a triangle theorem” (also known as the “triangle sum theorem” or “angle sum theorem”) states that the sum of the three interior angles of any triangle is always $180^{\circ}$.
What is the angle sum theorem in geometry? In Euclidean geometry, any triangle whether it is a right triangle, an obtuse triangle, or an acute triangle all have interior angles that add up to 180 degrees.
Recommended Games
Angle Sum Property of a Triangle Theorem
The angle sum property of a triangle theorem states that the sum of all three internal angles of a triangle is $180^{\circ}$. It is also known as the angle sum theorem or triangle sum theorem.

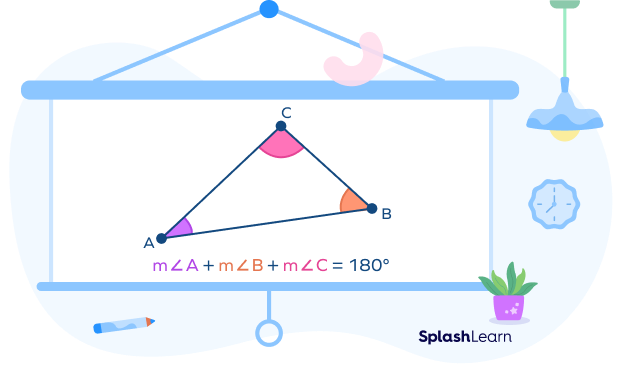
According to the angle sum theorem, in the above ABC,
$m\angle A + m\angle B + m\angle C = 180^{\circ}$
Example: In PQR, $\angle P = 60^{\circ}, \angle Q = 70^{\circ}$
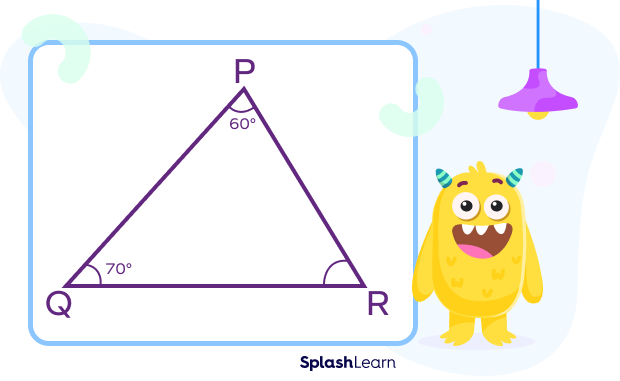
According to the angle sum theorem, in the above triangle PQR,
$m\angle P + m\angle Q + m\angle R = 180^{\circ}$
$60^{\circ} + 70^{\circ} + m\angle R = 180^{\circ}$
$130^{\circ} + m\angle R = 180^{\circ}$
$m\angle R = 50^{\circ}$
Recommended Worksheets
Triangle Sum Theorem Proof
In the figure given below, AB, BC, and CA represent three sides of triangle ABC. A, B, and C are the three vertices. $\angle A,\; \angle B,$ and $\angle C$ are the three interior angles of $\Delta ABC$.
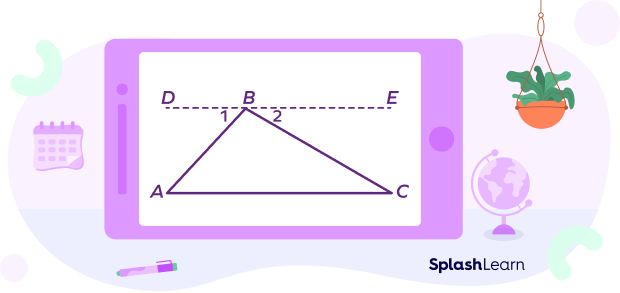
In ∆ABC, we have to prove that the sum of the angles $\angle A,\; \angle B,$ and $\angle C$ is $180^{\circ}$.
To prove: $m\angle A + m \angle B + m\angle C = 180^{\circ}$
Construction: Draw a line DE passing through the vertex B, which is parallel to the side AC.
At point B, two angles are formed, $\angle 1$ and $\angle 2$.
Since AB is a transversal for the parallel lines DE and AC, we have
$m\angle 1 = m\angle A$ (since the pair of alternate interior angles are equal)
Similarly, $m\angle 2 = m\angle C$.
Now, $m\angle 1,\; m\angle B,$ and $m\angle 2$ must add up to $180^{\circ}$ (angles on a straight line).
Thus, $\angle 1 + \angle B + \angle 2 = 180^{\circ}$… (I)
Since $\angle 1 = \angle A$ and $\angle 2 = \angle C$. … (II)
Substituting equation (II) in equation (I), we get
$m\angle A + m\angle B + m\angle C = 180^{\circ}$
Therefore, the sum of the three angles $\angle A,\; \angle B,$ and $\angle C$ is $180^{\circ}$.
Hence, the triangle sum theorem was proved.
Exterior Angle Theorem
The exterior angle theorem states that “an exterior angle of a triangle is equal to the sum of its two opposite interior angles.”
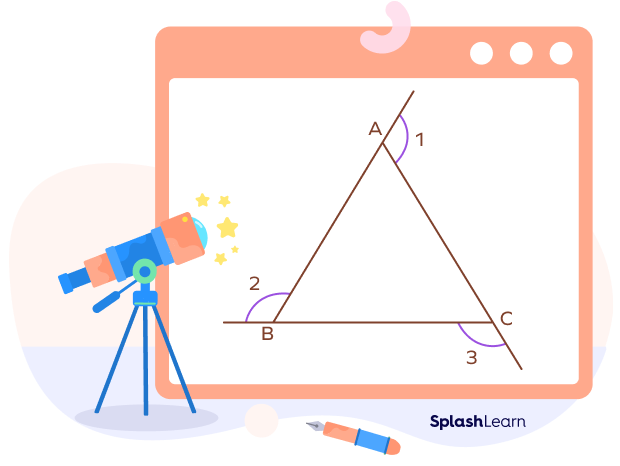
In the above triangle, $\angle A,\; \angle B,$ and $\angle C$ are the interior angles of the triangle ABC, and $\angle 1,\; \angle 2,$ and $\angle 3$ are the exterior angle.
$m\angle A + m\angle B + m\angle C = 180^{\circ}$ (angle sum property) … (I)
Also, $m\angle A + m\angle 1 = 180^{\circ}$ (linear pair angle) … (II)
From (I) and (II), we get
$m\angle A + m\angle 1 = m\angle A + m\angle B + m\angle C$
$m\angle 1 = m\angle B + m\angle C$
Similarly, we can derive for other two exterior angles,∠2 and ∠3 which is given by:
$m\angle 2 = m\angle A + m\angle C$
$m\angle 3 = m\angle A + m\angle B$
In summary:
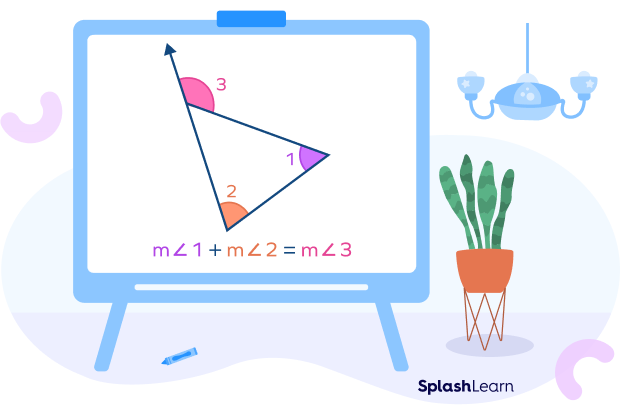
Facts about Angle Sum Property of a Triangle
- The theorem of angle sum property of triangles holds true for all types of triangles.
- The sum of all exterior angles of a triangle is equal to $360^{\circ}$.
- The sum of the lengths of any two sides of a triangle is always greater than the third side.
- A rectangle can be divided into two right triangles by drawing a line from one corner to the opposite corner.
- The study of the relationship between the sides and angles of triangles is known as trigonometry.
- Due to their high strength, triangle shapes are frequently utilized in construction.
- In North Carolina, there are three cities: Raleigh, Durham, and Chapel Hill, that are often referred to as the triangle.
- The sum of all exterior angles of a triangle is equal to $360^{\circ}$.
Conclusion
In this article, we have learned all about the angle sum property of a triangle, exterior angle property of a triangle, proof of triangle sum theorem, and some important facts about triangles.
Let’s solve a few triangle angle sum theorem examples and practice problems.
Solved Examples on Angle Sum Property of a Triangle
- In a triangle, ABC, if $m\angle A = 60^{\circ},\; m\angle B = 40^{\circ}$, then find the measure of angle $\angle C$.
Solution:
In $\Delta ABC,\; \angle A = 60^{\circ}$ and $\angle B = 40^{\circ}$
We know that the sum of angles in a triangle is $180^{\circ}$.
$\Rightarrow m \angle A + \angle B + \angle C = 180^{\circ}$
$\Rightarrow 60^{\circ} + 40^{\circ} + \angle C = 180^{\circ}$
$\Rightarrow \angle C = 180^{\circ} \;−\; ( 60^{\circ} + 40^{\circ})$
$\Rightarrow \angle C = 180^{\circ} \;−\; 100^{\circ}$
$\therefore \angle C = 80^{\circ}$
- One of the acute angles in a right-angled triangle is $40^{\circ}$. Using the angle sum theorem, determine the other angle.
Solution:
Let $\Delta ABC$ be given a right-angled triangle which is right-angled at B.
$\therefore \angle B = 90^{\circ}$
$m\angle A = 40^{\circ}$ and we have to find out $m\angle C$.
We know that the sum of angles in a triangle is $180^{\circ}$.
$\Rightarrow m \angle A + m \angle B + m \angle C = 180^{\circ}$
$\Rightarrow 40^{\circ} + 90^{\circ} + m\angle C = 180^{\circ}$
$\Rightarrow m \angle C = 180^{\circ} \;−\; (40^{\circ} + 90^{\circ})$
$\Rightarrow m \angle C = 180^{\circ} \;−\; 130^{\circ}$
$\therefore m \angle C = 50^{\circ}$
$\therefore m \angle A = m \angle C = 50^{\circ}$
- The measures of interior angles of a triangle are $(2x\;−\;20)^{\circ}, (3x\;−\;10)^{\circ}$, and $2x^{\circ}$, find the values of all three angles of the triangle.
Solution:
We know that the sum of angles in a triangle is $180^{\circ}$
$\Rightarrow (2x\;−\;20)^{\circ} + (3x\;−\;10)^{\circ} + 2x^{\circ} = 180^{\circ}$
$\Rightarrow (2x\;−\;20 + 3x\;−\;10 + 2x)^{\circ} = 180^{\circ}$
$\Rightarrow 7x\;−\;30 = 180$
$\Rightarrow 7x = 180 + 30$
$\Rightarrow 7x = 210$
$\Rightarrow x = 2107= 30$
$\Rightarrow$ Angles are $40^{\circ},\; 80^{\circ}$ and $60^{\circ}$.
- Is it possible to construct a triangle with internal angles $43^{\circ},\; 49^{\circ},$ and $91^{\circ}$?
Solution:
Given, measurements of angles $43^{\circ},\; 49^{\circ},$ and $91^{\circ}$.
Here, $43^{\circ} + 49^{\circ} + 91^{\circ} = 183^{\circ} 180^{\circ}$
We know, that, the sum of angles in a triangle is $180^{\circ}$
Hence, it is not possible to construct a triangle with measurements of angles $43^{\circ},\; 49^{\circ},$ and $91^{\circ}$.
- In the figure given below, determine the value of “x.”
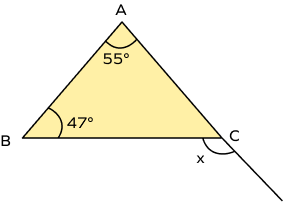
Solution:
In the above figure, $\angle x$ is an exterior angle and $\angle A = 55^{\circ}$ and $\angle B = 47^{\circ}$ are given as interior angles.
According to the exterior angle property,
an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
So, $\angle x = \angle A + \angle B = 55^{\circ} + 47^{\circ} = 102^{\circ}$
Hence, $x = 102^{\circ}$
Practice Problems on Angle Sum Property of a Triangle
Angle Sum Property of a Triangle: Definition, Theorem, Examples
If all angles of a triangle are congruent, then each angle measures ___.
Sum of all angles of a triangle is $180^{\circ}$. If all angles of a triangle are congruent, then we have
$3x = 180^{\circ}$. Thus, $x = 60^{\circ}$.
What is the sum of all interior angles of a triangle?
According to the angle sum theorem the sum of all three internal angles of a triangle is $180^{\circ}$.
Two angles of a triangle measure $30^{\circ}$ and $60^{\circ}$. The measure of the third angle is _____.
We know that the sum of angles in a triangle is $180^{\circ}$.
Thus, the measure of the third angle $= 180^{\circ} \;−\; (30^{\circ} + 60^{\circ}) = 90^{\circ}$
Find x.
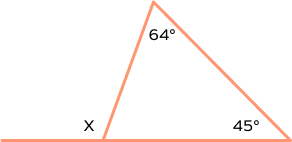
Exterior angle property of a triangle states that “an exterior angle of a triangle is equal to the sum of its two interior opposite angles.” Thus, $x = 109^{\circ}$
What is the sum of all exterior angles of a triangle?
Each exterior angle is the sum of its two opposite interior angles. Thus, the sum of all the exterior angles is two times the sum of all interior angles. The sum of all exterior angles of a triangle is equal to $360^{\circ}$.
Frequently Asked Questions on Angle Sum Property of a Triangle
What is the difference between the angle sum theorem and the exterior angle theorem?
The angle sum theorem states that the sum of all three internal angles of a triangle is 180°. Whereas the exterior angle theorem states that an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
Can we define the angle sum property for a quadrilateral?
Yes, we can define the angle sum property for a quadrilateral. According to the angle sum property of a quadrilateral, the sum of all four interior angles is 360 degrees.
What is the sum of all exterior angles of a quadrilateral?
The sum of all exterior angles of any polygon is equal to $360^{\circ}$. Hence the sum of all exterior angles of a quadrilateral is also equal to $360^{\circ}$
What is the formula for the angle sum property of a triangle?
We know that the sum of angles in a triangle is $180^{\circ}$. For $\Delta ABC$, the formula for the angle sum property of a triangle is $\angle A + \angle B + \angle C = 180^{\circ}$.
What Is the angle sum theorem for any polygon?
According to the angle sum theorem for any polygon, the sum of all interior angles is equal to $(n − 2) \times 180^{\circ}$, where n is the total number of sides of the polygon.