What Are Angles in a Quadrilateral?
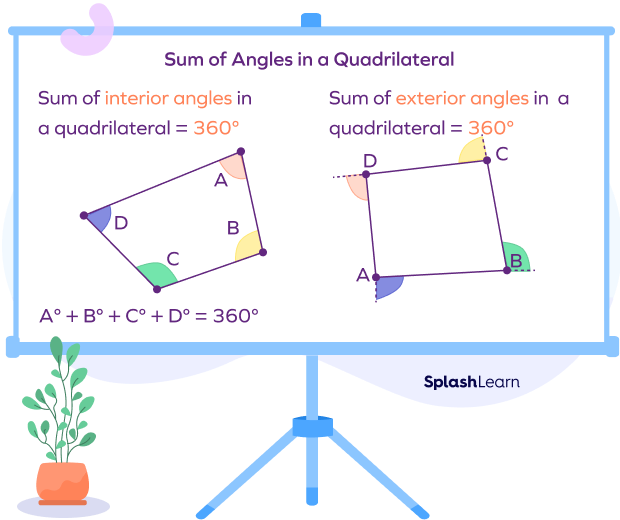
Angles in a quadrilateral are the four angles formed at each vertex. These angles are called interior angles of a quadrilateral.
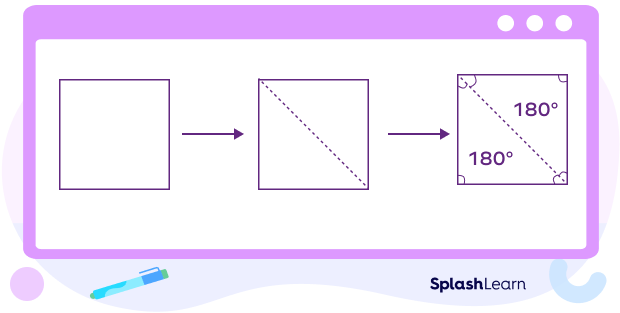
If you draw a diagonal, you can see that a quadrilateral gets divided into two triangles. We know the sum of the interior angles of a triangle is 180°. It follows that the sum of angles in a quadrilateral is 360°.
A quadrilateral is defined as a two-dimensional shape with four sides, four vertices, and four interior angles. A quadrilateral is a four-sided polygon shape formed by four non-collinear points.
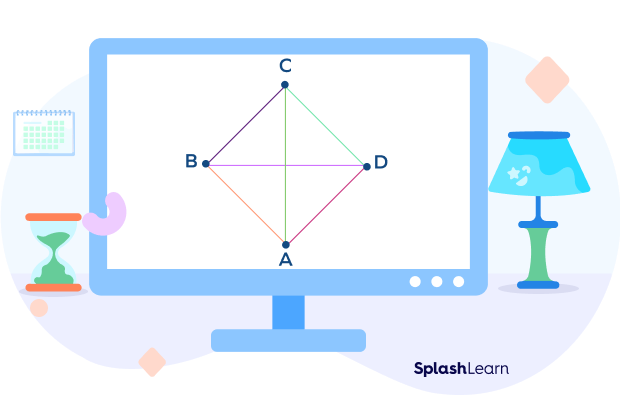
In the figure given above, ABCD is a quadrilateral.
AB, BC, CD, and DA are four sides of the quadrilateral.
A, B, C, and D are four vertices.
$\angle A, \angle B, \angle C$, and $\angle D$ are the four interior angles of this quadrilateral.
Recommended Games
Interior Angles and Exterior Angles of a Quadrilateral
There are 4 interior angles and 4 exterior angles in a quadrilateral.
Let’s understand the difference between the interior and exterior angles of a quadrilateral.
Interior Angles of a Quadrilateral
The sum of the interior angles of a quadrilateral is $360^{\circ}$. If there is one missing angle, we can use this property to find the measure of the missing angle.
Exterior Angles of a Quadrilateral
An exterior angle is formed by the intersection of any of the sides of a polygon and extension of the adjacent side. The sum of all the exterior angles of a quadrilateral is $360^{\circ}$.
Take a look at the quadrilateral ABCD. Angles 1, 2, 3, and 4 are the exterior angles. Angles A, B, C, and D are interior angles.
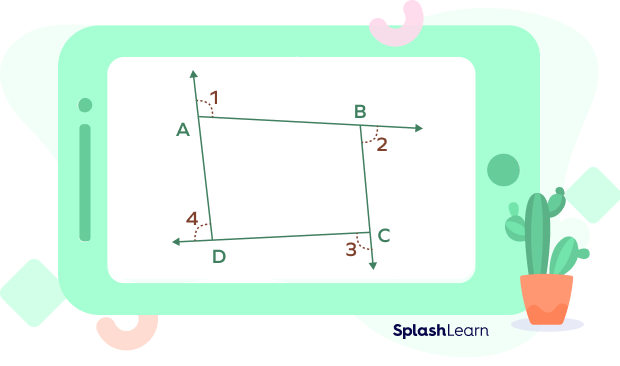
$\text{Interior Angle} + \text{Corresponding Exterior Angle} = 180^{\circ}$
$\angle A + \angle 1 = 180^{\circ}$
$\angle B + \angle 2 = 180^{\circ}$
$\angle C + \angle 3 = 180^{\circ}$
$\angle D + \angle 4 = 180^{\circ}$
Recommended Worksheets
Angles of a Quadrilateral Formulas
Let’s take a look at some basic formulas related to the interior and exterior angles of a quadrilateral.
Interior Angles Sum Property
The sum of interior angles of a polygon $= Sum = (n \;-\; 2) \times 180^{\circ}$
where “n” is the number of sides of the given polygon.
In a quadrilateral, $n = 4$.
Sum of interior angles of a quadrilateral $= (4 \;−\; 2) 180^{\circ}$
Sum of interior angles of a quadrilateral $= 360^{\circ}$
Note: If 3 angles of a quadrilateral are known, then the 4th angle can be calculated using the formula: $360^{\circ} \;-\;$ (Sum of the other 3 interior angles).
Interior angle and corresponding exterior angle
The sum of an interior angle and its corresponding exterior angle is always 180.
- Exterior angle $= 180^{\circ} \;-\;$ Corresponding Interior angle
- Interior angle $= 180^{\circ} \;-\;$ Corresponding Exterior angle
Exterior Angles Sum of a Quadrilateral
The sum of exterior angles of a quadrilateral is $360^{\circ}$.
Let angles W, X, Y, Z be the exterior angles corresponding to the interior angles A, B, C, D of a quadrilateral respectively.
Thus, $W + X + Y + Z = (180^{\circ} \;-\; A) + (180^{\circ} \;-\; B) + (180^{\circ} \;-\; C) + (180^{\circ} \;-\; D)$
$W + X + Y + Z = (180^{\circ} + 180^{\circ} + 180^{\circ} + 180^{\circ}) \;-\; (A + B + C + D)$
$W + X + Y + Z = (180^{\circ} + 180^{\circ} + 180^{\circ} + 180^{\circ}) \;-\; 360^{\circ}$
(…interior angles of a quadrilateral add up to $360^{\circ}$.)
$W + X + Y + Z = 360^{\circ}$
Thus, sum of exterior angles of a quadrilateral $= 360^{\circ}$
How to Find the Missing Angle in a Quadrilateral
Step 1: Use angle properties to determine interior angles.
Step 2: Add all known interior angles.
Step 3: Subtract the angle sum from $360^{\circ}$.
Example: Find the missing angle in the quadrilateral given below.
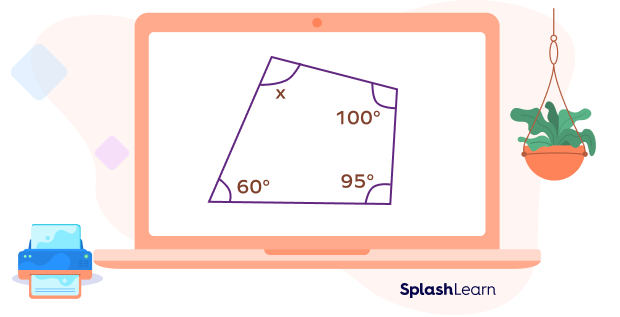
We know that the sum of the interior angles of a quadrilateral is $360^{\circ}$.
Adding the given 3 angles, we get
$100^{\circ} + 95^{\circ} + 60^{\circ} = 255^{\circ}$
Subtracting the sum from $360^{\circ}$, we get
$360^{\circ} \;-\; 255^{\circ} = x$
Thus, $x = 105$
Properties of Angles in a Quadrilateral
Let us look at the angle properties of a few common quadrilaterals.
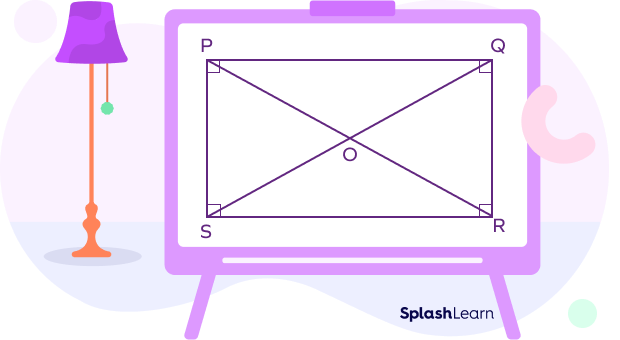
- All interior angles measure $90^{\circ}$.
- Diagonals bisect each other and form four angles at the point of intersection, two acute angles and two obtuse angles.
- The diagonals do not bisect the angles at vertices.
- Vertically opposite angles at the intersection of the diagonals.
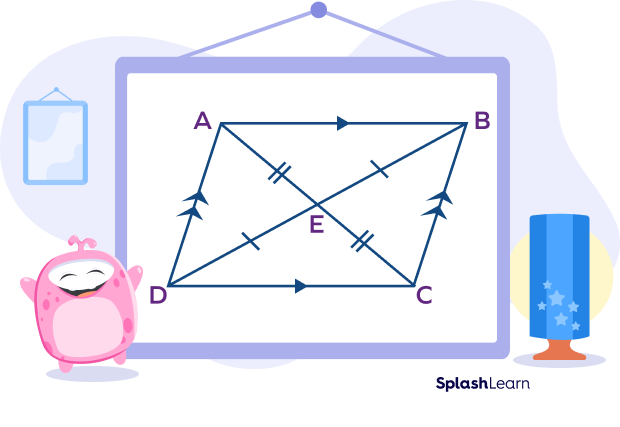
- Opposite angles are equal.
- Adjacent angles or consecutive angles are supplementary.
- Vertically opposite angles are formed at the intersection of the diagonals.
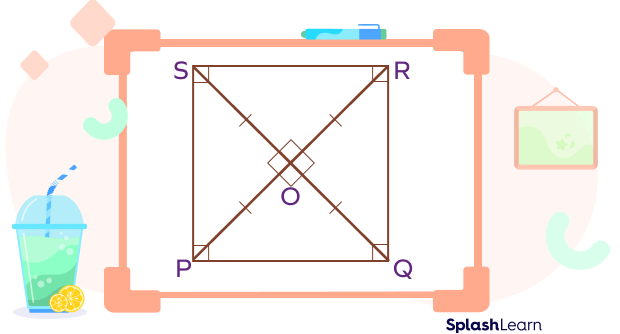
- All interior angles are congruent and measure $90^{\circ}$.
- Diagonals bisect each other at right angles.
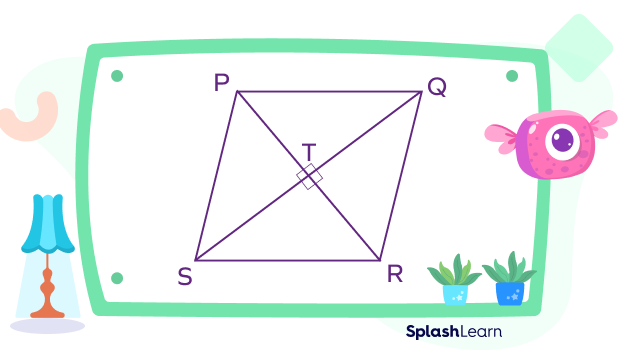
- Opposite angles are the equal.
- Adjacent angles are supplementary.
- Diagonals of a rhombus bisect each other at right angles.
- Diagonals of a rhombus bisect vertex angles.
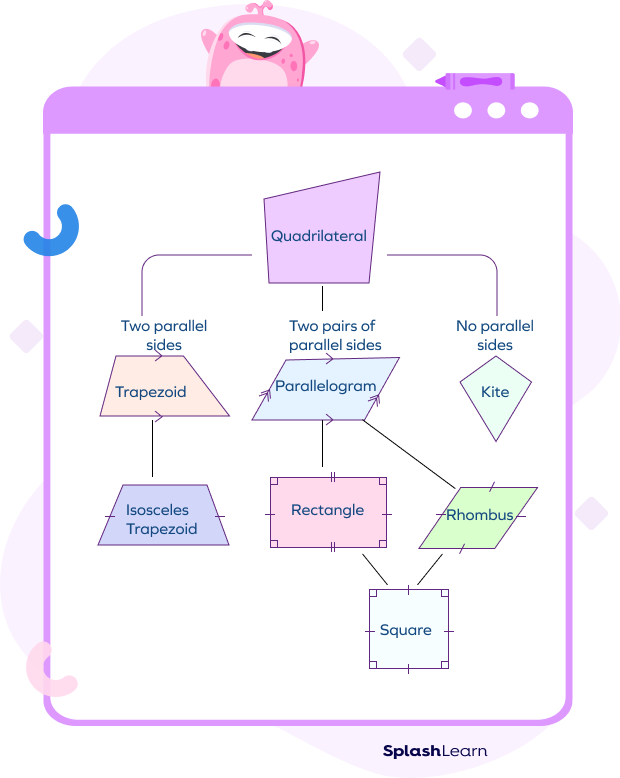
Quadrilateral Family
Take a look at the different types of quadrilaterals shown below. You can make an anchor chart to explore different properties of angles and sides in each of the given quadrilaterals & their types. Try it out!
Angles of a Quadrilateral Inscribed in a Circle
When a quadrilateral is inscribed in a circle, it is known as a cyclic quadrilateral or a chordal quadrilateral. It is a quadrilateral that has all its four vertices lying on the circumference of a circle. In a cyclic quadrilateral, the four sides of the quadrilateral form the chords of the circle.
The sum of opposite angles in a cyclic quadrilateral is $180^{\circ}$. In other words, opposite angles in a cyclic quadrilateral are supplementary.
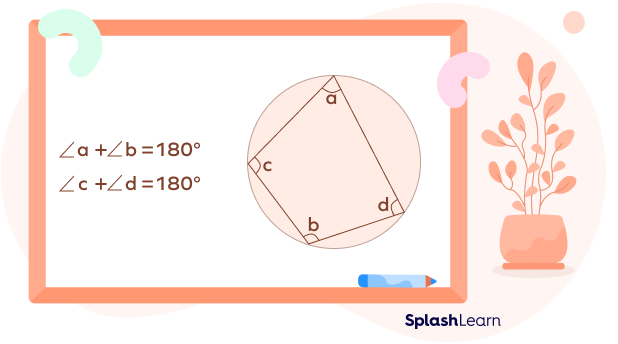
Facts about Angles in a Quadrilateral
Conclusion
In this article, we learned about the angles of a quadrilateral, its properties, interior and exterior angles, angles of a quadrilateral inscribed in a circle and some important formulas. Let us apply those formulas to solve some examples!
Solved Examples on Angles in a Quadrilateral
1. The angles of a quadrilateral are in the ratio of 1 : 2 : 3 : 4. Find the measure of each angle.
Solution:
The given angle ratio is 1 : 2 : 3 : 4.
Let the measures of the four angles be $x,\; 2x,\; 3x$, and $4x$.
The sum of interior angles of a quadrilateral is $360^{\circ}$.
$x + 2x + 3x + 4x = 360^{\circ}$
$10 x = 360^{\circ}$
$x = 36^{\circ}$
Thus, the measure of four angles are:
$x = 36^{\circ}$
$2x = 2(36^{\circ}) = 72^{\circ}$
$3x = 3(36^{\circ}) = 108^{\circ}$
$4x = 4(36^{\circ}) = 144^{\circ}$
Therefore, the angles of a quadrilateral are $36^{\circ},\;72^{\circ},\; 108^{\circ}$ and $144^{\circ}$.
2. Find the exterior angle of a quadrilateral whose corresponding interior angle is $60^{\circ}$.
Solution:
We know that the interior and exterior angles of a quadrilateral form a linear pair.
Thus, using the formula for the exterior angle of a quadrilateral,
Exterior angle $= 180^{\circ}\;-\;$ Interior angle
Exterior angle $= 180^{\circ} \;-\; 60^{\circ}$
$= 120^{\circ}$
The exterior angle of the quadrilateral is $120^{\circ}$.
3. Find the corresponding interior angle of a quadrilateral if its exterior angle is $104^{\circ}$.
Solution:
We know that the interior angle and the corresponding exterior angle of a quadrilateral form a linear pair.
Thus, using the formula for the exterior angle of a quadrilateral.
Exterior angle $= 180^{\circ} \;-\;$ Interior angle
Interior angle $= 180^{\circ} \;-\;$ Exterior angle
Interior angle $= 180^{\circ} \;-\; 104$
Interior angle $= 76^{\circ}$
The corresponding interior angle of the quadrilateral is $76^{\circ}$.
4. ABCD is a cyclic quadrilateral with center O. Find x.
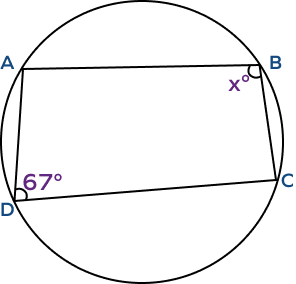
Solution:
ABCD is a cyclic quadrilateral.
Opposite angles of a cyclic quadrilateral sum up to 180.
Thus, $\angle D + x = 180^{\circ}$
$67^{\circ} + x = 180^{\circ}$
$x = 180^{\circ} \;-\; 67^{\circ}$
$x = 113^{\circ}$
Practice Problems on Angles in a Quadrilateral
Angles in a Quadrilateral - Definition, Properties, Examples, Facts
Which of the following is not a quadrilateral?
A triangle is not a quadrilateral as it has only three sides.
What is the sum of interior angles of a quadrilateral?
The interior angles of a quadrilateral always sum up to $360^{\circ}$.
Exterior angle and the corresponding interior angle of a quadrilateral add up to _______ angle.
Exterior angle and the corresponding interior angle of a quadrilateral form a $180^{\circ}$ angle.
If an interior angle of a quadrilateral is 70, then its corresponding exterior angle will be _______.
If an interior angle of a quadrilateral is 70, then its corresponding exterior angle will be, $180^{\circ} \;-\; 70^{\circ} = 110^{\circ}$.
The sum of the opposite angles of a cyclic quadrilateral is _______.
The opposite angles in a cyclic quadrilateral are supplementary. The sum of the opposite angles is equal to $180^{\circ}$.
Frequently Asked Questions on Angles in a Quadrilateral
Can all the angles of a quadrilateral be acute angles?
No, all angles of a quadrilateral cannot be acute angles. Acute angles are the angles less than $90^{\circ}$. If all the angles in a quadrilateral be less than $90^{\circ}$, the sum of interior angles will never be $360^{\circ}$. All angles of quadrilateral can be $90^{\circ}$, which will form a rectangle (or a square) but not less than $90^{\circ}$.
Is a triangle a quadrilateral?
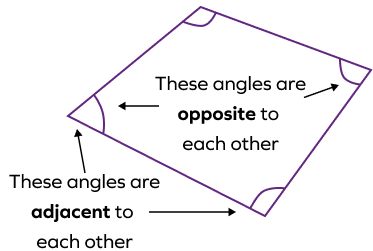
What are the adjacent angles and opposite angles in a quadrilateral?
Two angles of a quadrilateral having a common arm are called adjacent angles.
The opposite angles do not share a common arm. They lie diagonally opposite to each other.