Area of an Equilateral Triangle – Formula, Derivation, Examples

What Is the Area of an Equilateral Triangle?

Area of an equilateral is the region bounded within the three sides of the triangle. In other words, the area of an equilateral triangle is the total region enclosed within the boundary of the triangle. It is calculated using the simple formula $\frac{\sqrt{3}}{4} \times a^2$, where “a” is the length of the side. 

An equilateral triangle is a triangle in which all sides are equal and all interior angles are congruent. Each angle of an equilateral triangle measures $60^\circ$.

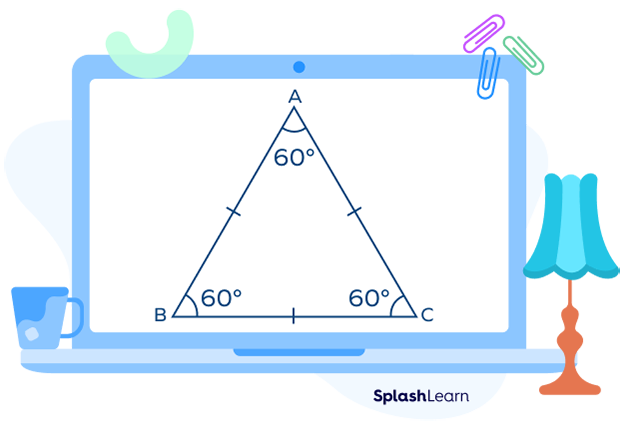
In the equilateral triangle ABC shown below, the area of the triangle is the green shaded region.

Area of an Equilateral Triangle Formula

The formula for area of equilateral triangle is given by:

$Area = \frac{\sqrt{3}}{4}\times(a)^2$ square units

where a is the length of the side of an equilateral triangle.

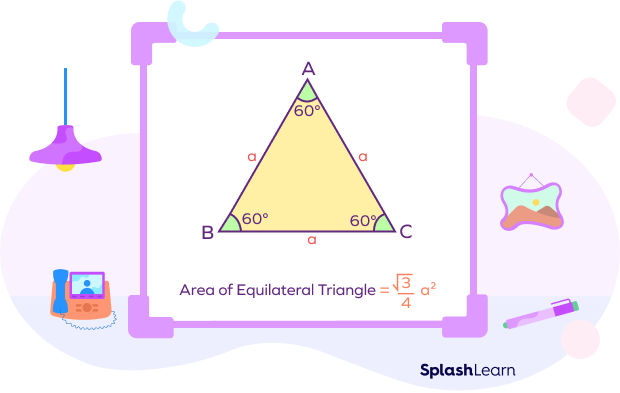
In the given triangle $ABC,\; AB = BC = CA = a$ units

Area of $\Delta ABC = \frac{\sqrt{3}}{4}\times(a)^2$

How to Find the Area of an Equilateral Triangle

To find the area of an equilateral triangle, simply substitute the length of the side in the following formula: 

$Area = \frac{\sqrt{3}}{4}\times(a)^2$

Simplify and give the appropriate unit.

Example: Find the area of an equilateral triangle side of 4 units. 

$Side = a = 4$ units

Area of an equilateral triangle $= \frac{\sqrt{3}}{4}\times(a)^2 = \frac{\sqrt{3}}{4}\times(4)^2 = 4\sqrt{3}$ square units

Derivation of Area of an Equilateral Triangle Formula

All the sides are equal and all the internal angles are 60° in an equilateral triangle. The formula to calculate the area of an equilateral triangle is given as,

Area of an equilateral triangle $= \frac{\sqrt{3}}{4}\times(a)^2$ square units

where,

$a =$ Length of each side of an equilateral triangle

We can derive the above formula to find the area of an equilateral triangle in the following three ways. 

Using Height

To find the area of any triangle, we require the length of the base and the height, since the general formula is:

Area of Triangle $= 12\times$ base $\times$ height

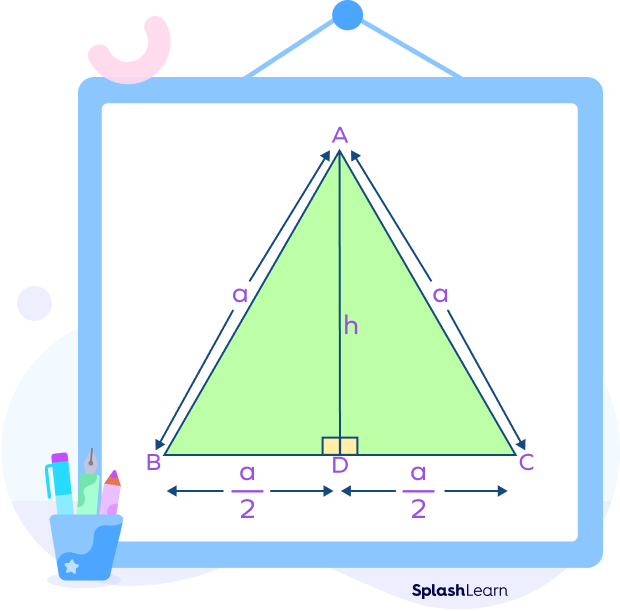
Calculating the height

First, we will calculate the height of an equilateral triangle in terms of the side length.

In the right triangle ABD:

Hypotenuse $= AB = a$ units

Base $= BD = \frac{a}{2}$ units

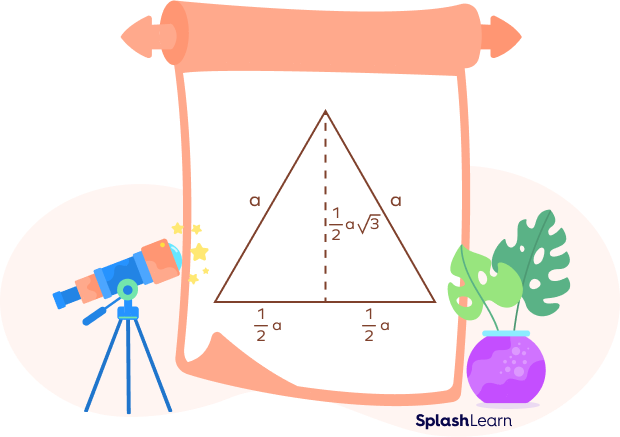
Based on Pythagoras’ Theorem

$AB^2 = BD^2 + AD^2$

$a^2 = \frac{a^2}{4} + AD^2$

$AD^2 = a^2\;-\;\frac{a^2}{4} = \frac{4a^2 – a^2}{4} = \frac{3a^2}{4} = \frac{\sqrt{3a}}{2}$ units

Height $= h = \frac{3a}{2}$ units

Area of Triangle $= 12\times$ base $\times$ height

Substitute the value of base and height in the formula

Area of equilateral triangle with height $\frac{\sqrt{3}a}{2}$ and base “a” can be given as 

$Area = \frac{1}{2} \times a \times \frac{\sqrt{3}a}{2}$

Area of Equilateral Triangle $= \frac{\sqrt{3}a^2}{4}$ square units

Using Heron’s Formula

When the lengths of the three sides of the triangle are known, Heron’s formula is used to find the area of a triangle. 

Consider a triangle ABC with sides a, b, and c. 

The Heron’s formula to find the area of the triangle is given by

\Area of a triangle $= \sqrt{s (s – a) (s – b) (s – c)}$

Where,

s is the semi-perimeter.

$s = \frac{a + b + c}{2}$

For equilateral triangle: $a = b = c$.

$s = \frac{a + a + a}{2} = \frac{3a}{2}$

Now, Area of equilateral triangle $= \sqrt{\frac{3a}{2}(\frac{3a}{2}\;-a)(\frac{3a}{2}\;-a)(\frac{3a}{2}\;-a)}$

Area of equilateral triangle $= \sqrt{\frac{3a}{2}\times\frac{a}{2}\times\frac{a}{2}\times\frac{a}{2}}$

Area of equilateral triangle $= \frac{\sqrt{3}a^2}{4}$ square units

Using Two Sides and Included Angle (SAS) Formula

How are the angles of an equilateral triangle related to its area? If two sides and the included angle between two sides is known, we use the following variations to find the area of a triangle. There are three ways to use the same formula based on which side and included angle are given.

• When sides “a” and “b” and the included angle C is known, the area of the triangle is: $Area = \frac{1}{2} \times ab \times sin C$
  
• When sides “b” and “c” and included angle A is known, the area of the triangle is: $Area = \frac{1}{2} \times bc \times sin\; A$

• When sides “a” and “c” and included angle B is known, the area of the triangle is: Area $= \frac{1}{2}\times ac \times sin\; B$

Consider an equilateral triangle ABC with sides a, b, and c.

What are the angles of an equilateral triangle? Each interior angle A, B, and C measures $60^\circ$. Thus, $\angle A = \angle B = \angle C = 60^\circ$. 

$\Rightarrow sin\; A = sin\; B = sin\; C$. 

Also, for an equilateral triangle, $a = b = c$

Area of $\Delta ABC = \frac{1}{2}\times b \times c \times sin\;(A) = \frac{1}{2} \times a \times b \times sin\; (C) = \frac{1}{2} \times a \times c \times sin\;(B)$.

Area of an equilateral triangle $= \frac{1}{2} \times a \times a \times sin\;(C)$ 

     $= \frac{1}{2} \times a^2 \times sin\;(60^\circ)$

      $= \frac{1}{2}\times a^2 \times \frac{\sqrt{3}}{2}$

Area of an equilateral triangle $= \frac{\sqrt{3}a^2}{4}$ square units

Properties of Equilateral Triangle

• All sides are equal in length.
• All angles are congruent. Each angle measures $60^\circ$. Thus, it is equiangular.
• It is a regular polygon.
• The area of an equilateral triangle is $\frac{\sqrt{3}a^2}{4}$.
• The perimeter of an equilateral triangle is 3a.
• In an equilateral triangle, the median, angle bisector, and perpendicular are all the same. 

Facts about Area of Equilateral Triangle

• You can simplify the Heron’s formula for the equilateral triangle as:

Area of an equilateral triangle $= \sqrt{s(s\;-\;a)^3}$

where $s = \frac{3a}{2}$

• Area of an equilateral triangle can also be calculated if the perimeter is known.

Perimeter of an equilateral triangle is 3a.

Find the side using this formula and substitute in the formula: Area $= \frac{\sqrt{3}a^2}{4}$

Solved Examples on Area of Equilateral Triangle

1. Find the area of an equilateral triangle whose perimeter is 12 inches.

Solution: 

Let the side of an equilateral triangle be a inches.

Perimeter $= 12$ in

Perimeter of an equilateral triangle $= 3a$

$\Rightarrow 3a = 12$ in

$\Rightarrow a = 4$ in

$Area = \frac{\sqrt{3}a^2}{4} = \frac{\sqrt{3}(4)^2}{4} = \frac{16\sqrt{3}}{4} = 4\sqrt{3}\; in^2$

2. If the area of an equilateral triangle is $16\sqrt{3}\; ft^2$, find the side of the triangle.

Solution: 

$Area = 16\sqrt{3}\; ft^2$

Let the side of an equilateral triangle be a ft.

$\frac{\sqrt{3}a^2}{4} = 16\sqrt{3}$

$\Rightarrow a^2 = 64$

$\Rightarrow a = 8\; ft$

Side of the triangle $= 8\; ft$

3. Find the area of an equilateral triangle whose height is $5\sqrt{3}$ units.

Solution: 

Height $= h = \frac{\sqrt{3}a}{2}$

$5\sqrt{3} = \frac{\sqrt{3}a}{2}$

$a = 10$ unit

$Area = \frac{\sqrt{3a^2}}{4} = \frac{\sqrt{3}(10)^2}{4} = \frac{100\sqrt{3}}{4} = 25\sqrt{3}$ square units

4. If the side of an equilateral triangle doubles, then by how much the area will increase? 

Solution: 

Let the side of an equilateral triangle be a units.

Original Area $= \frac{\sqrt{3}a^2}{4}$ square units

New side $= 2a$ units

New Area $= \frac{3(2a)^2}{4} = \sqrt{3}a^2$ square units

Increase in area $= \sqrt{3}a^2\;–\;\frac{\sqrt{3}a^2}{4} = \frac{3\sqrt{3}a^2}{4}$ square units

Practice Problems on Area of Equilateral Triangle

Frequently Asked Questions on Area of Equilateral Triangles