What Are Consecutive Angles?
Consecutive angles are formed on the same side of the transversal when two parallel lines are crossed by a transversal. Depending on their relative positions, either between or outside the parallel lines, they are categorized as consecutive interior angles and consecutive exterior angles, respectively.
In geometry, parallel lines can be defined as two lines in the same plane that are at equal distances from each other and never meet. They may be horizontal lines or vertical lines. Transversal is a line that intersects two parallel lines in two distinct points.
Recommended Games
Consecutive Angles: Definition
When two parallel lines are intersected by a transversal, then the pairs of angles formed on the same side of the transversal (either in the interior or the exterior region of two parallel lines) are called “consecutive angles.”
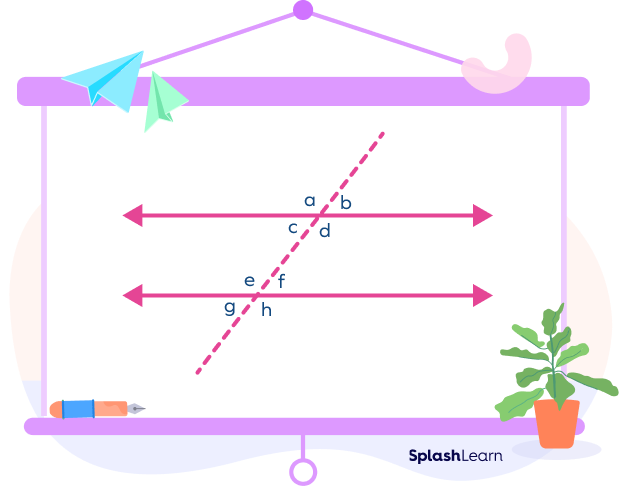
In the given figure, the pairs of consecutive angles are
- ∠c and ∠e
- ∠d and ∠f
- ∠b and ∠h
- ∠a and ∠g
Recommended Worksheets
Types of Consecutive Angles
Based on the intersecting position of parallel lines and the transversal, there are two types of consecutive angles.
- Consecutive interior angles
- Consecutive exterior angles
Consecutive Interior Angles
The angles which lie on the interior part of the two parallel lines (between two parallel lines), on the same side of the transversal are known as consecutive interior angles. The consecutive interior angles are also referred to as “co-interior angles” or “same-side interior angles.”
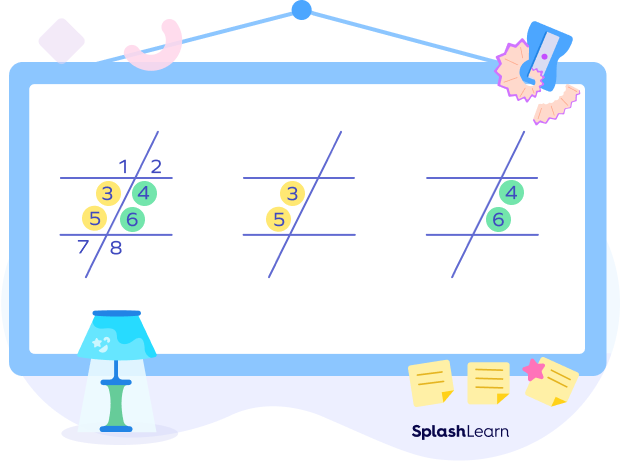
In the given figure, the pair of consecutive interior angles are highlighted in the same colors.
- ∠3 and ∠5
- ∠4 and ∠6
Consecutive Exterior Angles
The angles which lie on the exterior part of the two parallel lines (outside the two parallel lines) and on the same side of the transversal are known as consecutive exterior angles.
The consecutive exterior angles are also referred to as co-exterior angles or same-side exterior angles. Consecutive exterior angles are supplementary.
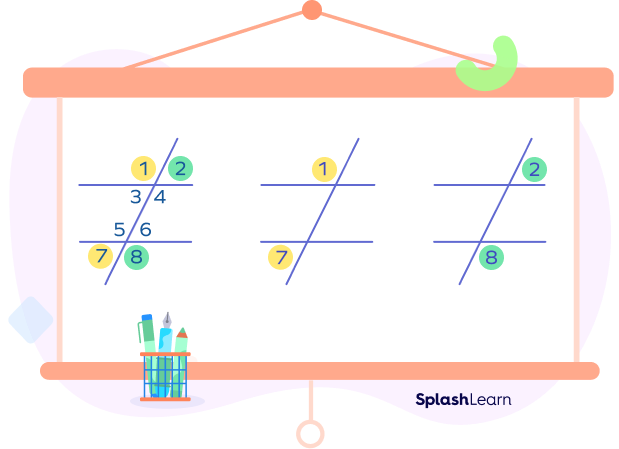
In the given figure, the pairs of consecutive exterior angles are highlighted in the same colors.
- ∠1 and ∠7
- ∠2 and ∠8
Consecutive Angles Theorem
Consecutive angles theorem states that if two parallel lines are cut by a transversal, then the pairs of consecutive interior angles formed are supplementary.
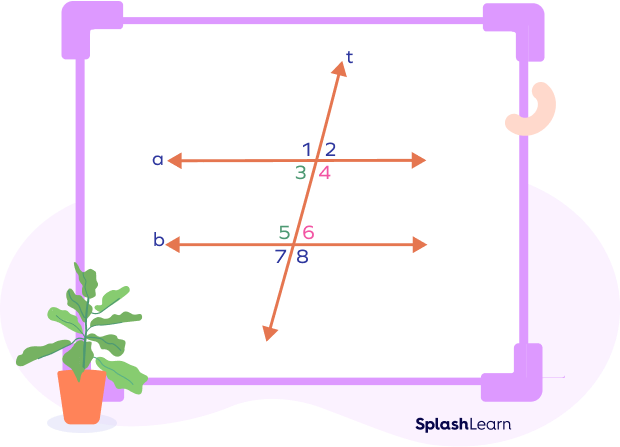
From the above figure, we can write
∠3 + ∠5 = 180o
∠4 + ∠6 = 180o
Converse of Consecutive Angles Theorem
If two lines are cut by a transversal such that the consecutive interior angles are supplementary (add up to 180 degrees), then the lines are parallel.
Consecutive Angles in a Parallelogram
In a parallelogram, each pair of adjacent angles represent consecutive angles.
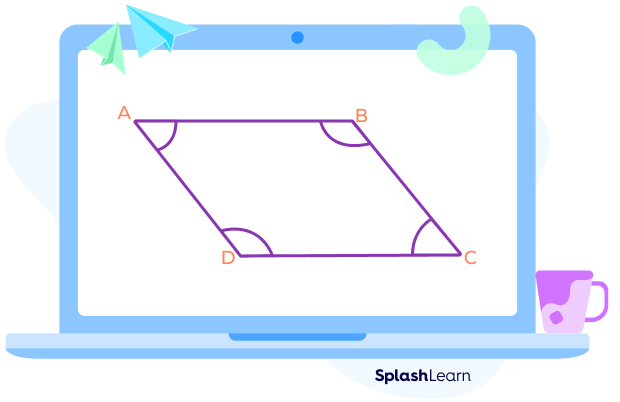
Here, the pair of adjacent angles are as follows
- ∠A and ∠B
- ∠C and ∠D
- ∠A and ∠D
- ∠B and ∠C
In a parallelogram, opposite sides are parallel.
Two parallel lines AB and CD are cut by two transversals AD and BC.
Also, two parallel lines AD and BC are cut by transversals AB and CD.
If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles formed are supplementary. Thus, the sum of adjacent angles of a parallelogram is equal to 180.
- ∠A + ∠B = 180o
- ∠C + ∠D = 180o
- ∠A + ∠D = 180o
- ∠B + ∠C = 180o
Facts about Consecutive Angles
- If the two lines cut by a transversal are not parallel, there is no special relation between the consecutive angles.
- Consecutive exterior angles formed by two parallel lines cut by a transversal are also supplementary.
Conclusion
In this article, we learned about the consecutive angles, their types, theorems, and facts. We also learned about consecutive angles in a parallelogram. Let’s solve a few examples and MCQs for better comprehension.
Solved Examples on Consecutive Angles
- Identify the pairs of consecutive interior and exterior angles in the given figure.
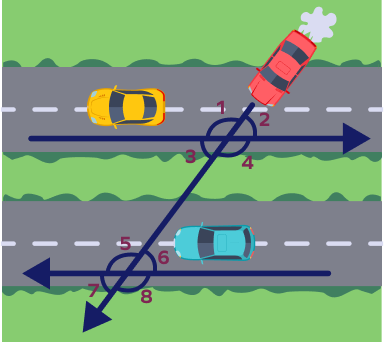
Solution:
Pairs of consecutive interior angles: ∠3 and ∠5; ∠4 and ∠6.
Pairs of consecutive exterior angles: ∠1 and ∠7; ∠2 and ∠8.
- A pair of consecutive interior angles formed by lines p and q are 106 and 73. Check whether two lines ‘p’ and ‘q’ are parallel or not.
Solution:
For the lines p and q to be parallel, the given consecutive interior angles must satisfy the converse of the consecutive angles theorem.
In simple words, if the sum of the measures of given angles is 180o, the lines are parallel.
Here, 106o + 73o = 179o ≠ 180o.
Hence, the lines p and q are not parallel.
- In the given figure, the lines l and m are two parallel lines. Find the value of ‘x’.
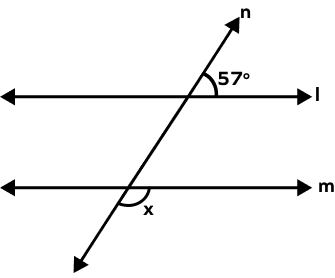
Solution:
In the figure, angles x and 57o form pairs of consecutive exterior angles. Thus, their sum must be equal to 180.
x + 57o = 180o
x = 180o − 57o
Therefore, x = 123o
- In the given figure, the lines l and m are two parallel lines, find the value of ‘y’.
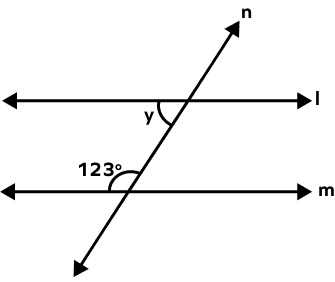
Solution:
In the figure, angles y and 123o form a pair of consecutive interior angles. Thus, they add up to 180o.
y + 123o = 180o
y = 180o − 123o
Therefore, x = 57o.
4. If the two consecutive interior angles of a parallelogram are given by (x + 60)o and (2x + 30)o, then which type of parallelogram is it?
Solution:
We know that the sum of interior angles of a parallelogram = 180
So, (x + 60)o + (2x + 30)o = 180o
3x + 90 = 180
3x = 180 − 90
3x = 90
Therefore, $x = \frac{90}{3} = 30$
Thus, (x + 60)o = (30 + 60)o = 90o
(2x + 30)o = [2(30) + 30]o = 90o
Opposite angles of a parallelogram are equal. Thus, all interior angles are right angles.
Thus, it is a rectangle.
Practice Problems on Consecutive Angles
Consecutive Angles – Definition, Types, Theorem, Examples, FAQs
The sum of consecutive angles of a parallelogram is always equal to ___ degrees.
The sum of consecutive angles of a parallelogram is always 180 degrees.
There are _____ types of consecutive angles formed when two parallel lines are intersected by a transversal.
There are two types of consecutive angles formed (interior and exterior) when two parallel lines are intersected by a transversal.
In the figure given below, the line ____ is the transversal.
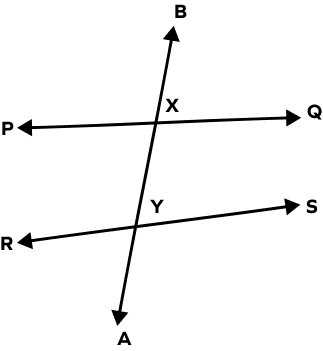
Transversal lines are those that cross two or more lines at different points. Hence, in the given figure AB is a transversal line.
Identify the type of angles shown in the figure.
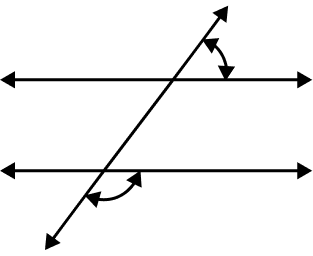
From the figure, it is clear that the angles shown are pairs of consecutive exterior angles.
What is the sum of adjacent angles in a parallelogram?
The sum of adjacent angles in a parallelogram is supplementary. It is because they represent a pair of consecutive interior angles.
Frequently Asked Questions about Consecutive Angles
Are consecutive angles congruent?
No, consecutive angles are not congruent. They are supplementary if the two lines crossed by the transversal line are parallel
Are consecutive angles always supplementary?
Consecutive angles are supplementary if the two lines crossed by the transversal line are parallel.
What is the sum of consecutive interior angles?
The sum of exterior consecutive angles is equal to 180o if the two lines cut by the transversal are parallel to each other.
What are consecutive angles in a parallelogram?
In a parallelogram, each pair of adjacent angles represents consecutive angles.
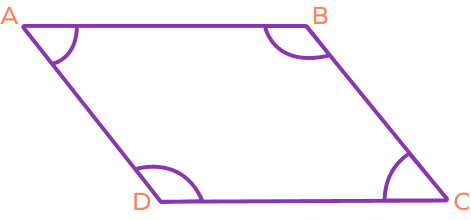
In the,e above figure, the pairs of consecutive angles are
- ∠A and ∠B
- ∠C and ∠D
- ∠A and ∠D
- ∠B and ∠C.
Their sum is always 180o.





























