What Are Corresponding Sides in Geometry?
Corresponding sides are the pair of matching sides that are placed at the same spot in two different shapes.
Corresponding sides and corresponding angles are compared to study similarity and congruence. Corresponding parts are the parts that appear in identical places in two similar shapes. Then, what does the term “corresponding sides” mean in math? Corresponding sides are a pair of matching sides that are in the same spot in two different shapes. The two different shapes must be either congruent or similar.
In geometry, finding the congruence and similarity involves comparing corresponding sides and corresponding angles of the polygons. Let us learn more about corresponding sides.
Example: Consider two congruent triangles shown in the image below. The corresponding sides are shown in the same color.

When two triangles are congruent, their corresponding sides and corresponding angles are also congruent.
When two triangles are similar, their corresponding sides are in proportion, and corresponding angles are congruent.
Recommended Games
Corresponding Sides: Definition
Corresponding sides are the sides that are in the same position in two different shapes or polygons.
- If the two polygons are congruent, they have the same shape and size. The corresponding sides & the corresponding angles are congruent.
- When the two polygons are similar, the polygons have the same shape but different size. The corresponding angles are congruent and the corresponding sides are proportional.
Recommended Worksheets
How to Find Corresponding Sides
If you superimpose two shapes, the sides that overlap on each other will be corresponding sides. Corresponding sides touch the same two angle pairs of two figures. Also, the angles formed by two corresponding sides are corresponding angles.
Note that rotating the similar or congruent shapes does not change the corresponding sides (or angles). It only becomes a little tricky for us to identify the correspondence.
When we mention the congruence or similarity of two triangles, we maintain the order of the corresponding sides and angles while writing. It is because that’s how we identify the corresponding sides or angles that are congruent.
If we say that $\Delta LMN$ is similar to $\Delta XYZ$, we can easily identify the corresponding sides and corresponding angles using the given order.
| Triangles | Corresponding Sides | Corresponding Angles | ||||
|---|---|---|---|---|---|---|
| $\Delta LMN$ | LM | MN | LN | $\angle L$ | $\angle M$ | $\angle N$ |
| $\Delta XYZ$ | XY | YZ | XY | $\angle X$ | $\angle Y$ | $\angle Z$ |
Example 1: The corresponding sides of two triangles are shown in the same color.
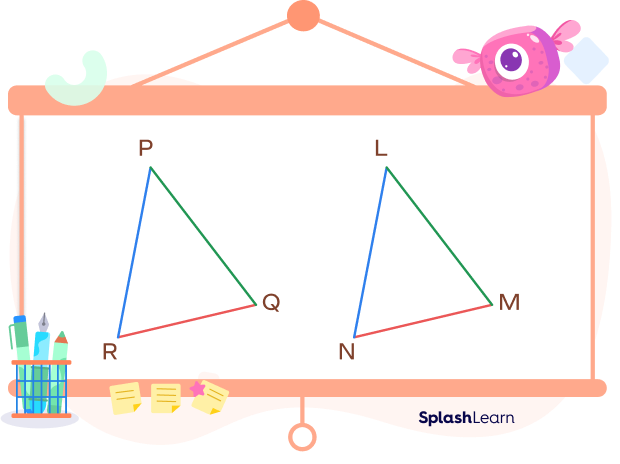
Side PQ corresponds to the side LM.
Side QR corresponds to the side MN.
Side PR corresponds to the side LN.
| Triangles | Corresponding Sides | |||
|---|---|---|---|---|
| $\Delta LMN$ | LM | MN | LN | |
| $\Delta PQR$ | PQ | QR | PR | |
Example 2: Consider two polygons.
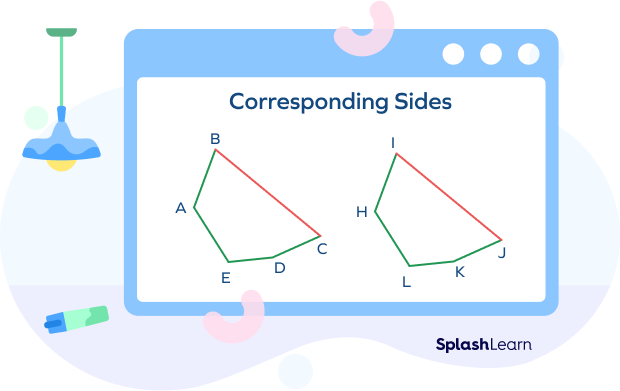
$\overline {AB}$ corresponds with $\overline {EF}$.
$\overline {BC}$ corresponds with $\overline {FG}$.
$\overline {CD}$ corresponds with $\overline {GH}$.
$\overline {AD}$ corresponds with $\overline {EH}$.
Difference between Congruent Triangles and Similar Triangles
Let’s first learn about congruent triangles and similar triangles.
Congruent Triangles
Congruent triangles are two triangles that have the same shape and same size. In two congruent triangles, the corresponding angles are equal and the corresponding sides are also equal.
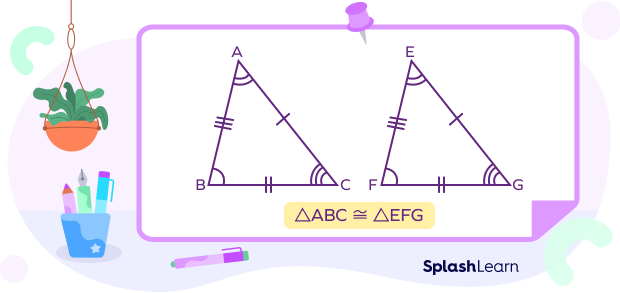
Take a look at the diagram given below.
In $\Delta ABC$ and $\Delta EFG$,
$AB = EF,\; BC = FG,\; AC = EG$
$\angle A = \angle E,\; \angle B = \angle F,\; \angle C = \angle G$
Thus, $\Delta ABC$ is congruent to $\Delta EFG$.
Similar Triangles
Similar triangles are two triangles that have the same shape but are not the same size. In two similar triangles, the corresponding angles are equal and the corresponding sides have the same ratio. Take a look at the image given below:

In $\Delta ABC$ and $\Delta PQR$,
$\frac{AB}{PQ} = \frac{BC}{QR} = \frac{AC}{PR}$ (Corresponding sides are in proportion.)
and
$\angle A = \angle P,\; \angle B = \angle Q,\; \angle C = \angle R$
Thus, $\Delta ABC$ is similar to $\Delta PQR$.
Now, let’s take a look at the difference between congruent and similar triangles.
| Congruent Triangles | Similar Triangles |
|---|---|
| They have the same shape and size. | They have the same shape but are not necessarily the same size. |
| Corresponding sides are congruent. | Corresponding sides are in proportion. |
| Corresponding angles are congruent. | Corresponding angles are congruent. |
| They are identical to each other. | They are resized versions of each other. |
| All congruent triangles are similar. | All similar triangles need not be congruent. |
| Symbol: $\cong$ | Symbol: $\sim$ |
Corresponding Sides in Similar Triangles
When two triangles are similar, they have the same shape but differ in size. Now, the question is: Are corresponding sides equal? The corresponding sides are equal in the case of congruent triangles. The corresponding sides of two similar triangles are always in “proportion.” The common ratio of the corresponding sides of two similar figures is called the scale factor.
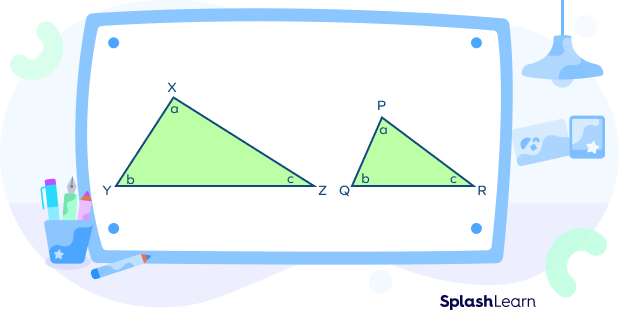
Consider the similar triangles XYZ and PQR.
Here, $\angle X\; \cong\; \angle P,\; \angle Y\; \cong \;\angle Q,\; \angle Z \; \cong \;\angle R$
- XY and PQ are corresponding sides.
- XZ and PR are corresponding sides.
- YZ and QR are corresponding sides.
Corresponding Sides in Right Triangles
Two right triangles are similar if the hypotenuse and one of the legs are proportional to their corresponding sides in the other right triangle. This is known as HL theorem (Hypotenuse-Leg Theorem). Consider the two right triangles ABC and DEF in the image given below. Their corresponding sides are shown in the same color.
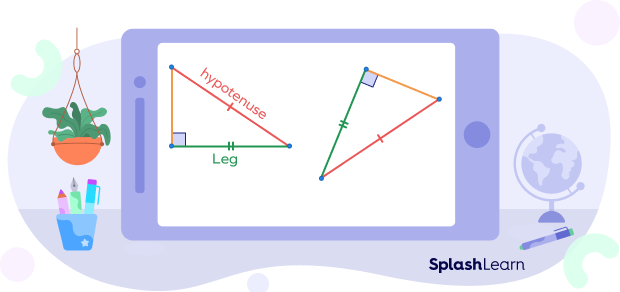
In the given two right triangles, the hypotenuse and one leg is congruent with the hypotenuse and leg of the other right triangle. Therefore, the two right triangles are similar, and their corresponding sides are proportional.
Facts about Corresponding Sides
- Corresponding sides are a pair of matching sides that are in the same spot in two different shapes.
- When two triangles are similar, the ratios of the lengths of their corresponding sides are equal.
- Two triangles are considered to be congruent if all their corresponding angles and sides are equal.
- If a polygon is congruent, it is also similar but a similar polygon need not be congruent.
Conclusion
In this article, we learned about the corresponding sides of similar triangles and right triangles. Let’s solve some examples based on corresponding sides for better understanding.
Solved Examples on Corresponding Sides
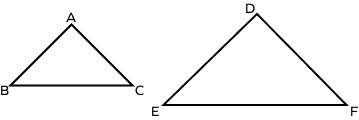
1. Observe the similar triangles given below. What are the 3 pairs of corresponding sides?
Solution:
The triangles $\Delta ABC$ and $\Delta DEF$ are similar.
The side AB corresponds to the side DE.
The side BC corresponds to the side EF.
The side AC corresponds to the side DF.
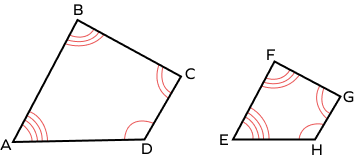
2. Given that the quadrilateral ABCD is similar to quadrilateral EFGH, which side corresponds to the side EH?
Solution:
Quadrilateral ABCD is similar to quadrilateral EFGH.
Maintaining the order of vertices, we can identify that the side in ABCD corresponding to the side EH in EFGH is side AD.
AB corresponds to EF.
BC corresponds to FG.
CD corresponds to GH.
AD corresponds to EH.
4. $\Delta UVW \;\sim\; \Delta XYZ$. IF $UV = 3,\; VW = 4,\; UW = 5$ and $XY = 12$. Find $XZ$ and $YZ$.

Solution:
We know that $\Delta UVW\; \sim \;\Delta XYZ$.
Thus, $\frac{UV}{XY} = \frac{UW}{XZ} = \frac{VW}{Yz}$
$\frac{3}{12} = \frac{5}{XZ} = \frac{4}{YZ}$
Thus, solving the equations, we get
$XZ = UW \times 4 = 20$
$YZ = VW \times 4 = 16$
Therefore, $XZ = 20$ and $YZ = 16$.
Practice Problems on Corresponding Sides
Corresponding Sides - Definition, Solved Examples, Facts, FAQs
In similar triangles, the corresponding sides _________.
Similar triangles are two triangles that have the same shape but not of the same size. In two similar triangles, the corresponding angles are equal and the corresponding sides have the same ratio.
Which is the correct congruence statement?
Corresponding sides: $LM = PR,\; LN = PQ$, and $MN = QR$
Corresponding angles: $\angle L = \angle P,\; \angle N = \angle Q,\; \angle M = \angle R$
Thus, $\Delta LNM\;\cong\;\Delta PQR$.
$\Delta UVW\;\sim\;\Delta UEC$. Name the corresponding side of VW.
$\Delta UVW$ and $\Delta UEC,\; UV$ corresponds to UE, VW corresponds to EC and UW corresponds to UC.
$\Delta ABC\;\cong\;\Delta PQR$ such that $m\angle A = 65^\circ$. What is $m\angle P$?
If two triangles are congruent, the corresponding angles and sides are congruent.
$\angle P$ corresponds to $\angle A$.
Thus, in $\Delta ABC$ and $\Delta PQR,\; \angle A = \angle P = 65^\circ$.
Frequently Asked Questions on Corresponding Sides
Are corresponding angles always equal?
No, all corresponding angles are not equal. The corresponding angles formed when a transversal intersects two parallel lines are equal.
Do similar shapes have proportional areas?
When two triangles are similar, not only do their angles and sides are in proportion, but also their perimeters, altitudes, angle bisectors, areas, and other characteristics are in proportion as well.
How do you find the area of the similar triangles?
According to the area of similar triangles theorem, “The ratio of the areas of two similar triangles is equal to the square of the ratio of any pair of their corresponding sides.” Let’s take a look at an example. Consider two similar triangles$\Delta ABC$ and$\Delta PQR$,
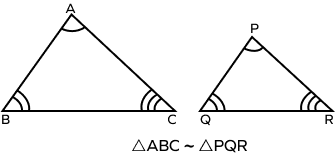
According to the theorem for areas of similar triangles, we have
$\frac{Area\; of\;\Delta ABC}{Area\; of\;\Delta PQR} = \frac{(AB)^2}{(PQ)^2} = \frac{(BC)^2}{(QR)^2} = \frac{(AC)^2}{(PR)^2}$
What are the various theorems to prove triangle similarity?
There are three theorems used to prove triangle similarity.
1. AA: Two pairs of corresponding angles are equal.
2. SSS: Three pairs of corresponding sides are proportional.
3. SAS: Two pairs of corresponding sides are proportional and the corresponding angles included between them are equal.
Are the circles congruent if they have the same diameter?
Two circles are known to be congruent if their radius is equal to each other. The length of a diameter is twice the radius. Therefore, congruent circles have the same diameter. On the other hand, all circles are similar since they have the same shape but different sizes.





























