Decimal Place Value – Definition, Examples, Practice Problems, FAQs

What are Decimal Numbers?

Decimals help express small units of money and to measure mass, length, and capacity in higher units.

75 dollars 25 cents can be expressed using decimal numbers like $\$$75.25.

A decimal number consists of a whole number and a fractional part, separated by a decimal point. The decimal point is the dot that appears between the full number and the fractions.

For example, 25.5 is a decimal number.

Here, 25 is the whole number, and 5 is the fraction. “.” is the decimal point. 

For whole numbers, we know how to place the digits in the place value chart. In this article, we will explore the place and the value of places after the decimal point.

What is Decimal Place Value?

Depending upon the position of a digit in a number, it has a value called its place value. 

The value of the digits in the decimal (base ten) system is based on the number ten. 

In a place value chart, as we move from right to left, the value of each place increases by 10 times.  

The value of the tens place is ten times that of the ones place. The value of the hundreds place is ten times that of the tens place and so on.

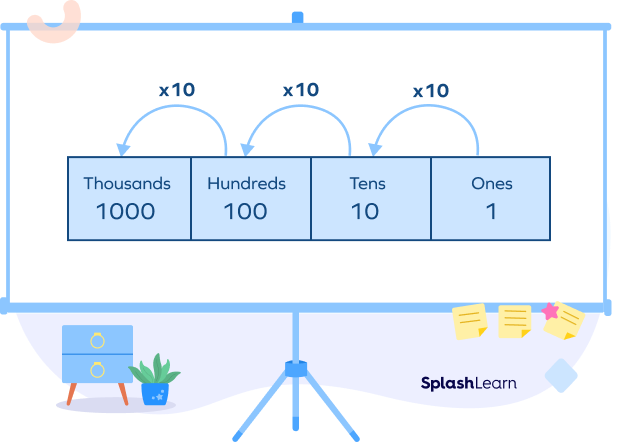
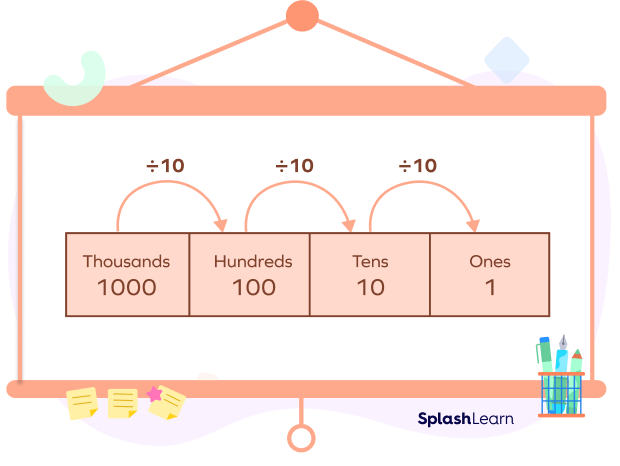
When we move from one place to the next place on the right side of a place value table, the place becomes one-tenth 110 of its previous place.

The value of the hundreds place is 110 of the thousands place. The value of tens place is 110 of hundreds place. The value of ones place is 110 of the tens place.

On moving to the right of the ones place, we get a place ten times smaller than 1, that is, one-tenth or “tenths”, which is a fractional part. Hence, we separate it by a decimal point. So, our place value chart with decimals looks like this:

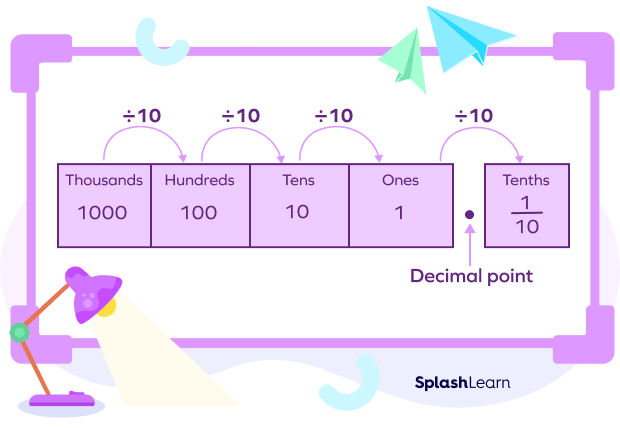
The place to the right of “tenths” is the “hundredths” and the place to the right of “hundredths” is the “thousandths”. 

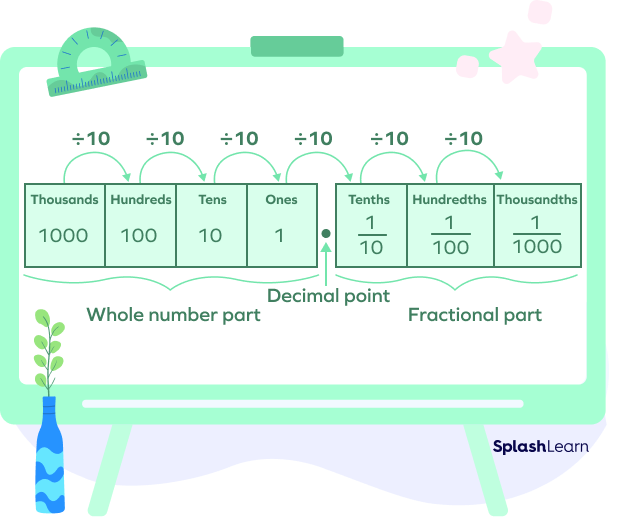
Now, we have our decimal place value chart ready.This decimal chart helps us find the place value of the digits in a decimal number.

We separate the whole number part and decimal part by putting a dot (point) called a decimal point.

In a decimal number chart, the place values of all digits are represented, including those before and after the decimal point.

Writing Decimal Numbers in the Decimal Place Value Chart

Decimal number may contain a whole number part and a fractional part (decimal part).

In case the decimals consist of only one part that is a decimal part or the whole part, we will write zero in the whole or decimal part.

For example:

$.23 = 0.23$

$42 = 42.0$

Let’s write the following decimals in the place value table:

452.123; 1000.788; 3.409; 33.005; 710.01

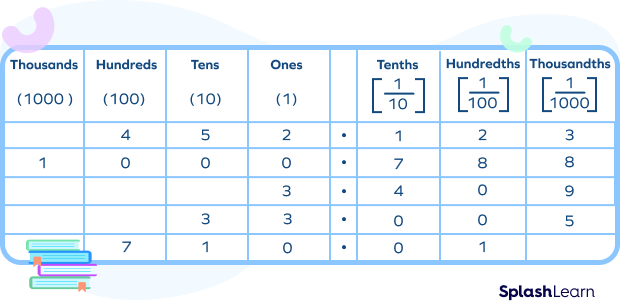
This helps us in identifying the place of each digit of the decimal number.

Now each place is associated with a value. Let’s learn about the place value of decimal numbers.

Understanding the Decimal Place Value Chart

When looking at the decimal place value chart, you can see that place values before the decimal point begin with ones, then tens, hundreds, and so on, but place values following the decimal point begin with tenths, then hundredths, then thousandths, and so on.

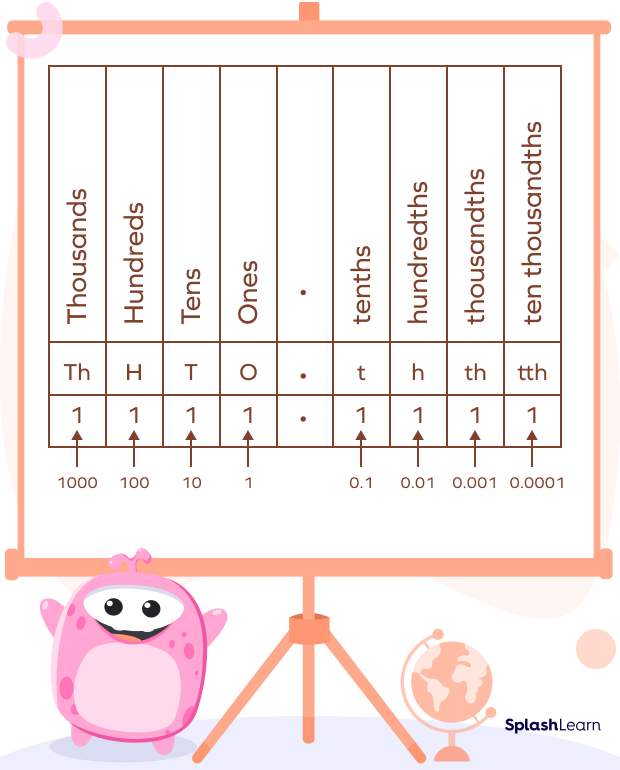
The fraction part of the number is represented by the digits following the decimal point of a decimal number.

For example, the number 0.46 is made up of 4 tenths and 6 hundredths.

This can also be written as $0.46 = 0.4 + 0.06$.

In other words, it means, $0.46 = 4/10 + 6/100$.

Conclusion

The face value of a digit in a number is the value of the digit itself, which does not depend on the place of the digit, whereas the place value is the value of that digit in that place, which changes as the place of the digit changes.

Solved Examples On Decimal Place Value

Example 1: Identify the digit at thousandths place for the given decimals.

(a) 14.005

(b) 172.231

(c) 14.3

Solution:

First, write the decimal in place value chart. Then look at the digit at the thousandths place.

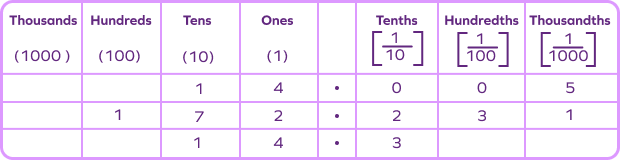
1. 5
2. 1
3. 0, as there is no digit at the thousandths place for the given decimal number.

$14.3 = 14.300$   

Example 2: Identify the place value of the underlined digits.

(a) 893.871

(b) 36.657

(c) 0.045

Solution:

First, write the number in a place value chart.

Then, look at the place of the digit and find its place value.

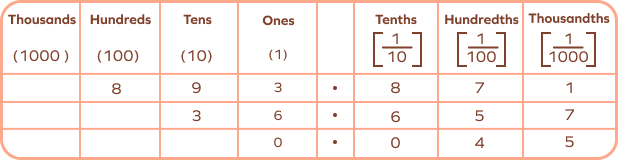
1. The digit 7 is in the hundredths place. Therefore, its place value is 7 hundredths or 0.07.
2. There are two 6s in the given decimal, but the underlined 6 is in the ones place. Therefore, its place value is 6 ones or 6.
3. The digit 5 is in the thousandths place. Therefore, its place value is 5 thousandths or 0.005.

Example 3:  In 1.5327, which digit is in the hundredths place?

The hundredths place represents the position of the second digit after the decimal point.

In 1.5327, the second digit after the decimal point is 3. 

Example 3: What is the sum of the digit at the tenths and hundredths place in the number 354.168?

Solution:

Digit at the tenths place $= 1$

Digit at the hundredths place $= 6$

Sum of digits $= 1 + 6 = 7$

Example 3:  In 1.5327, which digit is in the hundredths place?

The hundredths place represents the position of the second digit after the decimal point.

In 1.5327, the second digit after the decimal point is 3.

Practice Problems On Decimal Place Value

Frequently Asked Questions On Decimal Place Value