Fraction Rules – Definition with Examples

What Are Fractions?

Fractions are the mathematical representation of equal parts of a whole or a collection. When we divide a whole into a certain number of equal parts, we get a fraction of the whole. The numerator or the top number represents the number of selected or shaded parts of a whole, whereas the denominator or the bottom number represents the total number of parts.

For example, in the fraction $\frac{4}{5}$, the numerator is 4 and the denominator is 5.

What Are Fraction Rules?

Fraction rules are the set of rules we apply for working with fractions. The primary rule of fractions states that the value of a fraction does not change when its numerator and denominator are multiplied by the same non-zero number. It can be applied to add or subtract two fractions. Basic rules for fraction to add, subtract, multiply, and divide fractions are given below.

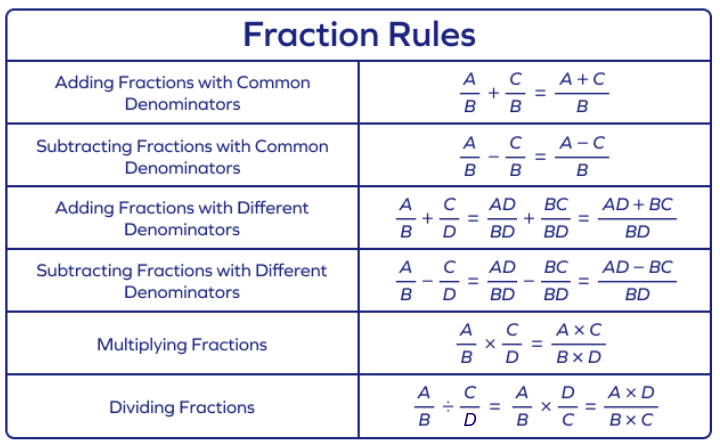
Today, we will explore and learn about how to solve a problem on fractions using the rules for fractions. Let us get right to it.

Rules for Addition and Subtraction

Like whole numbers, integers and decimals, we can also add and subtract two or more fractions. To add or subtract, we must have fractions with the same denominator. 

If the denominators are already the same then we just need to either add or subtract the numerators. 

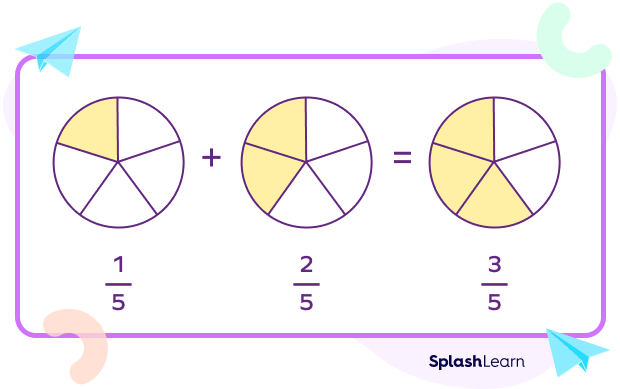
Addition: $\frac{A}{B} + \frac{C}{B} = \frac{A+C}{B}$. For example, $\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}$ 

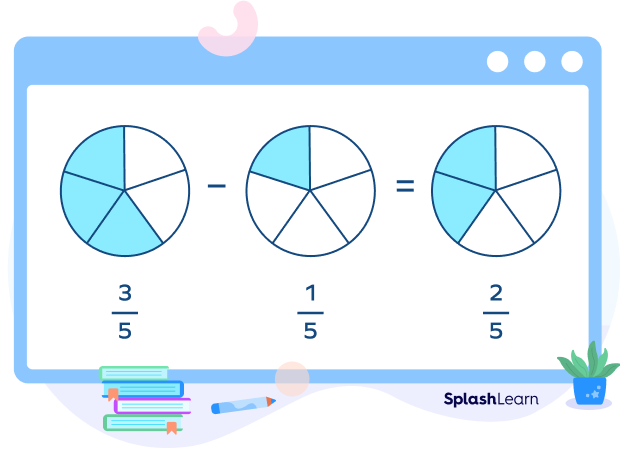
Subtraction:  $\frac{A}{B} – \frac{C}{B} = \frac{A – C}{B}$

For example,  $\frac{3}{5} – \frac{1}{5} = \frac{3 – 1}{5} = \frac{2}{5}$

If the denominators of the fractions are different, then we need to convert them to like fractions (same denominator). This can be done by finding the common denominator and converting each fraction so that they have a common denominator.

Adding and subtracting fraction rules are as follows.

Addition: $\frac{A}{B} + \frac{C}{D} = \frac{AD}{BD} + \frac{CB}{BD} = \frac{AD  +  CB}{BD}$

Subtraction: $\frac{A}{B} – \frac{C}{D} = \frac{AD}{BD} – \frac{CB}{BD} = \frac{AD – CB}{BD}$ 

For example, $\frac{1}{5} + \frac{2}{7} = \frac{1 \times 7}{5 \times 7} + \frac{2 \times 5}{7 \times 5} = \frac{7}{35} + \frac{10}{35} = \frac{7 + 10}{35} = \frac{17}{35}$

Rule for Multiplication

Multiplication of two or more fractions does not require a common denominator like addition and subtraction does. To multiply fractions, simply multiply the numerators and multiply the denominators.

$\frac{A}{B} \times \frac{C}{D} = \frac{AC}{BD}$ 

For example: $\frac{4}{7} \times \frac{2}{6} = \frac{8}{42} = \frac{4}{21}$

The following are some rules we need to keep in our mind while multiplying two fractions. 

• Unlike fractions can be multiplied.
• A numerator can only be multiplied by a numerator, and a denominator can only be multiplied by a denominator.
• To multiply mixed numbers, we can change them to improper fractions and multiply.

Rule for Division

To divide one fraction by another, we must write the reciprocal of the second term or fraction and then multiply with the first.

$\frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \times \frac{D}{C} = \frac{AD}{BC}$ 

For example, $\frac{1}{2} \div \frac{3}{5} = \frac{1}{2} \times \frac{5}{3} = \frac{5}{6}$

Rule for Conversion between Mixed Number and Improper Fraction

To convert a mixed number to an improper fraction, multiply the whole part by the denominator and add the product to the numerator. The denominator remains unchanged.

$A\frac{b}{c} = \frac{A \times c + b}{c}$

For example, $2\frac{3}{8} = \frac{2 \times 8 + 3}{8} = \frac{19}{8}$

To convert an improper fraction to a mixed number, divide the numerator by the denominator. The mixed number is the quotient, and the remainder is divided by the denominator.

For example, $\frac{5}{4} = 1\frac{1}{4}$

Rule for Comparing Fraction

To compare like fractions (with like denominators), just compare the numerators. In such a case, the fraction with a greater numerator is greater.

For example, $\frac{23}{5} \lt \frac{27}{5}$

To compare fractions with like numerators, compare the denominators. The fraction with a greater denominator is smaller.

For example, $\frac{23}{5} \gt \frac{23}{7}$

To compare fractions with unlike denominators, either convert them to a decimal or transform them to a common denominator, then compare them.

Conclusion

In this article, we learned about fraction rules. There are different rules to do operations with fractions. To read more such informative articles on other concepts, visit our website! We, at SplashLearn, are on a mission to make learning fun and interactive for all students.

Solved Examples

1. Add $\frac{2}{9}$ and $\frac{5}{36}$.

Solution: 

$\frac{2}{9} + \frac{5}{36}$

LCM 9 and $36 = 36$

Find the fraction equivalent to $\frac{2}{9}$ with denominator 36.

$\frac{2}{9} + \frac{5}{36} = \frac{2 \times 4} {9 \times 4} + \frac{5}{36} = \frac{8}{36} + \frac{5}{36} = \frac{13}{36}$

2. Multiply $\frac{11}{13}$ and $\frac{143}{121}$.

Solution: 

$\frac{11}{13} \times \frac{143}{121} = \frac{1573}{1573} = 1$ 

3. Divide $\frac{3}{10}$ by $2\frac{2}{5}$. 

Solution:

Division by a fraction is the same as multiplying by its reciprocal.

$\frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \times \frac{D}{C} = \frac{AD}{BC}$

$\frac{3}{10} \div 2\frac{2}{5} = \frac{3}{10} \div \frac{12}{5} = \frac{3}{10} \times \frac{5}{12} = \frac{15}{120} = \frac{1}{8}$

Practice Problems

Frequently Asked Questions