Simplify Mixed Numbers – Definition With Examples

What is Simplify in Maths?

Simplify means to make it simple. In mathematics, to simplify or simplification is to reduce the expression/fraction/problem in a simpler form. It makes the problem easy for calculations and solving.

Mixed Numbers

A mixed number is a combination of a whole number, and a proper fraction. It generally represents a number between any two whole numbers. 

Look at the given image, it represents a fraction that is greater than 1 but less than 2. It is thus a mixed number.

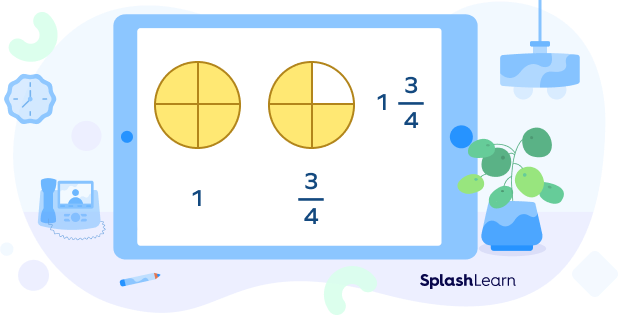
Some other examples of mixed numbers are: 

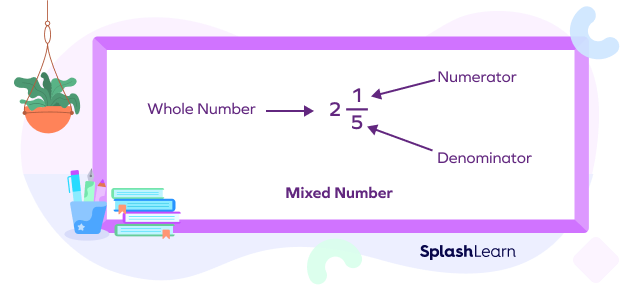
Parts of a Mixed Number

A mixed number is formed by combining three parts: a whole number, a numerator, and a denominator. The numerator and denominator are part of the proper fraction that makes the mixed number.

Simplify Mixed Numbers

Simplify mixed numbers is to convert a mixed number into reduced form. A mixed number is said to be in its simplest form if the highest common factor, i.e., the HCF of its fractional part is 1. 

On simplifying mixed numbers, the value of the fraction remains the same. We can say that the simplified mixed number and the actual mixed number are equivalent fractions. 

Converting Mixed Numbers into Improper Fractions

Suppose the mixed number is $2\frac{1}{3}$.

Step 1: We will multiply the denominator with the whole number part. 

Here, 3 × 2 = 6.

Step 2: We will add the numerator to the product obtained in step 1. 

Here, 6 + 1 = 7.

Step 3: We will write the value obtained in step 2 over the denominator. This will be the new numerator while the denominator will remain the same. 

Here, we get $\frac{7}{3}$. 

How to Simplify Mixed Numbers Step by Step

Let the fraction be $9\frac{4}{8}$.

Step 1: We will look at the fractional part.  

In this example, we will look at $\frac{4}{8}$ and will keep the whole part as it is. 

The factors of 4 and 8 are

Factors of 4: 1, 2 and 4

Factors of 8: 1, 2, 4 and 8.  

Step 2: Determine the highest common factors of numerator and denominator. The highest common factor of 4 and 8 is 4.

Step 3: Divide the numerator and denominator by the highest common factor. The fraction obtained by dividing is in the simplest form. Let’s divide by 4, then 

$\frac{4 \div 4}{8 \div 4}$ = $\frac{1}{2}$.

Hence, the mixed number is $9\frac{1}{2}$.

Let the fraction be $4\frac{12}{15}$.

Step 1: The first step is to write the factors of numerator and denominator of the fractional part keeping the whole number aside. 

The factors of 12 and 15 are

Factors of 12: 1, 2, 3, 4, 6 and 12.

Factors of 15: 1, 3, 5 and 15. 

Step 2: The next step is to determine the HCF of the numerator and denominator. The greatest common factor of 12 and 15 is 3. 

Step 3: The final step is to divide the numerator and denominator by the HCF. The fraction obtained after dividing is in the simplest form.

$\frac {12 \div 3}{15 \div 3}$ = $\frac{4}{5}$

Thus, we get $4 \frac{4}{5}$. 

Solved Examples

Solution: Factors of 24: 1, 2, 3, 4, 6, 8, 12 and 24

Example 1: Simplify $2 \frac{24}{36}$.

Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18 and 36

HCF of 24 and 36 = 12

$\frac {24 \div 12}{36 \div 12}$ = $\frac{2}{3}$

So, $ 2 \frac{24}{36}$ = $2 \frac{2}{3}$

Example 2: Add: $ 1 \frac {4}{8} $ and $ 4 \frac {16}{32}$.

Solution: $ 1 \frac{4}{8}$

HCF (4, 8) = 4

$ \frac {4 \div 4}{8 \div 4} $= $ \frac {1}{2}$ , So we get $ 1 \frac{1}{2}$ = $ \frac{3}{2}$

$ 4 \frac {16}{32}$

HCF (16, 32) = 16

$ \frac {16 \div 16}{32 \div 16}$ = $ \frac {1}{2} $, So we get $ 4 \frac{16}{32} $ = $4 \frac{1}{2}$ = $ \frac {9}{2}$

$ \frac {3}{2}$ + $ \frac {9}{2}$ = $ \frac {3 + 9}{2}$ = $\frac{12}{2}$ = 6

Example 3: Write the mixed number for the following shaded part and simplify it. 

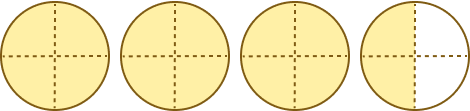
Solution: There are 3 whole shaded parts and the fraction shaded in fourth figure is $ \frac {2}{4}$.

So, the mixed number = $ 3 \frac {2}{4}$

HCF (2, 4) = 2 $ \frac {2 \div 2} {4 \div 2}$ = $ \frac {1}{2}$ , So we get $ 3 \frac{2}{4}$ = $ 3 \frac {1}{2}$

Practice Problem

Frequently Asked Questions