Unlike Numerators – Definition With Examples

What Is a Numerator?

When numbers are written in the form of a fraction, it can be represented as a/b, where a is the numerator and b is the denominator. A numerator is the part of a fraction that is above the line and represents the number of parts out of the whole, whereas a denominator is the total numbers of the parts. 

For example, in the fraction $\frac{3}{5}$, the numerator is 3 and the denominator is 5. 

In the above image, the number of shaded parts out of total parts are 5. So, the numerator is 5 and the denominator is 6. 

What Are Unlike Numerators

When the numerators of two or more fractions are not same or like, the numerators are called unlike numerators irrespective of whether the denominators are same or not. 

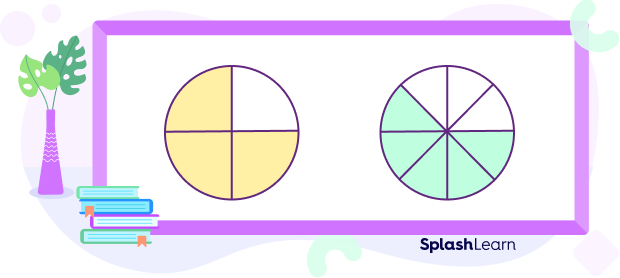
In the first figure, the number of shaded parts is 3. So, the numerator is 3. In the second figure, the number of shaded parts is 5. So, the numerator is 5. Hence, both are the fractions with unlike numerators.

How to Convert Unlike Numerators to Like Numerators

For making the numerators of two or more fractions same or like, we can find out the LCM of the numerators and then multiply the numerators with relevant numbers. It becomes easy to compare if there are like numerators. 

For example, we have to compare $\frac{3}{4} and \frac{9}{11}$.

LCM (3, 9) = 9

$\frac{3\times3}{4\times3}=\frac{9}{12} and \frac{9}{11}$

For comparing 912 and 911, we just have to look at the denominator. 

Since 12 > 11

 $\frac{9}{12}\lt\frac{9}{11}\Rightarrow\frac{3}{4}\lt\frac{9}{11}$

Operations on Fractions with Unlike Numerators

• When the denominator is the same or when the fractions are like fractions. When the denominator of the fractions are the same, then only the numerators get compared, added, or subtracted.

A. Comparing Fractions 

Let us compare fractions with unlike numerators

$\frac{3}{5} and \frac{4}{5}$. 

Since the denominators are the same, only numerators, i.e., 3 and 4 will be compared.

We can say that $\frac{3}{5}\lt\frac{4}{5} as 3 \lt 4$. 

B. Add Fractions

Let us add $\frac{3}{5} and \frac{4}{5}$. 

Since the denominators are the same, only numerators, i.e., 3 and 4 will be added.

We can say that $\frac{3}{5}+\frac{4}{5}=\frac{3+4}{5}=\frac{7}{5}=1\frac{2}{5}$ 

C. Subtract Fractions

Let us subtract $\frac{4}{5} and \frac{3}{5}$. 

Since the denominators are the same, only numerators, i.e., 4 and 3 will be subtracted.

We can say that $\frac{4}{5}-\frac{3}{5}=\frac{4-3}{5}=\frac{1}{5}$ 

• When the denominators are different or the fractions are unlike fractions.

When the denominator of the fractions are different, then we complete the operations, i.e., comparing, adding, and subtracting the fractions by finding the LCM of denominators and multiplying the numerator and denominator by the relevant numbers. 

A. Comparing Fractions

Let us compare $\frac{3}{4} and \frac{5}{7}$. 

LCM (4, 7) = 28

$\frac{3\times7}{4\times7}=\frac{21}{28};\frac{5\times4}{7\times4}=\frac{20}{28}$ 

Since the denominators are the same now, 

We can say that $\frac{21}{28}\gt\frac{20}{28} as 21 > 20\Rightarrow\frac{3}{4}\gt\frac{5}{7}$ 

B. Add Fractions

Let us add 34 and 57. 

$\frac{3}{4} + \frac{5}{7} = \frac{21}{28}+\frac{20}{28}=\frac{41}{28}=1\frac{13}{28}$

C. Subtract Fractions

Let us subtract $\frac{3}{4} and \frac{5}{7}$. 

$\frac{3}{4}-\frac{5}{7} = \frac{21}{28}-\frac{20}{28}=\frac{1}{28}$

Ascending Order of Fractions with Unlike Numerators

Ascending is also known as increasing. So, when numbers have their values listed from smallest to largest, we say that it is in ascending order. Ascending order for the fractions with unlike numerators can be calculated by finding LCM of the numerators if the denominators are also unlike. In case of like fractions, we just have to compare the numerator. 

For example, write these numbers in ascending order: $\frac{2}{5},\frac{3}{7},\frac{5}{14},\frac{1}{10}$.

LCM of 2, 3, 5 and 1 = 30

$\frac{2\times15}{5\times15}=\frac{30}{75},\frac{3\times10}{7\times10}=\frac{30}{70},\frac{5\times6}{14\times6}=\frac{30}{84},\frac{1\times30}{10\times30}=\frac{30}{300}$

Greater the denominator, smaller the fraction.

$\frac{30}{300}\lt\frac{30}{84}\lt\frac{30}{75}\lt\frac{30}{70}$

Descending Order of Fractions with Unlike Numerators

Descending  is also known as decreasing. So when numbers have their values from largest to smallest, we say that it is in descending order. Descending order for the fractions with unlike numerators can be calculated by finding LCM of the numerators if the denominators are also unlike. In case of like fractions, we just have to compare the numerator. 

For example, write these numbers in descending order: $\frac{2}{5},\frac{3}{7},\frac{5}{14},\frac{1}{10}$.

LCM of 2, 3, 5 and 1 = 30

$\frac{2\times15}{5\times15}=\frac{30}{75},\frac{3\times10}{7\times10}=\frac{30}{70},\frac{5\times6}{14\times6}=\frac{30}{84},\frac{1\times30}{10\times30}=\frac{30}{300}$

Smaller the denominator, greater the fraction.

$\frac{30}{70}\gt\frac{30}{75}\lt\frac{30}{84}\lt\frac{30}{300}$

Solved Examples

Example 1. Write the following fractions in descending order. 

$\frac{1}{4},\frac{2}{3}and\frac{5}{6}$

Solution: The smaller the denominator, the greater the fraction when the fractions have same or like numerators.

LCM(1, 2, 5) = 10

$\frac{1\times10}{4\times10}=\frac{10}{40},\frac{2\times5}{3\times5}=\frac{10}{15},\frac{5\times2}{6\times2}=\frac{10}{12}$

$12\lt15\lt40$

$\frac{10}{12}\gt\frac{10}{15}\gt\frac{10}{40}$ 

$56\gt23\gt14$

2. Add: $\frac{2}{3}+\frac{1}{5}+\frac{3}{4}$.

Solution: LCM(3, 5 and 4) = 60

$\frac{2\times20}{3\times20}=\frac{40}{60};\frac{1\times12}{5\times12}=\frac{12}{60};\frac{3\times15}{4\times15}=\frac{45}{60}$

$\frac{40}{60}+\frac{12}{60}+\frac{45}{60}=\frac{97}{60}=1\frac{37}{60}$

3. Write the following fractions in ascending order:

$\frac{2}{5},\frac{7}{9}and\frac{14}{25}$

Solution:The greater the denominator, the smaller the fraction when the fractions have same or like numerators.

LCM(2, 7, 14) = 14

$\frac{2\times7}{5\times7}=\frac{14}{35},\frac{7\times2}{9\times2}=\frac{14}{18},\frac{14}{25}$

$35 \gt 25 \gt 18$ 

$\frac{14}{35}\lt\frac{14}{25}\lt\frac{14}{18}\Rightarrow\frac{2}{5}\lt\frac{14}{25}\lt\frac{7}{9}$

Practice Problems

Frequently Asked Questions