Angle Definition
When two rays intersect at a common endpoint, they form an angle. The common endpoint is called the vertex, and the rays are called the arms of the angle.
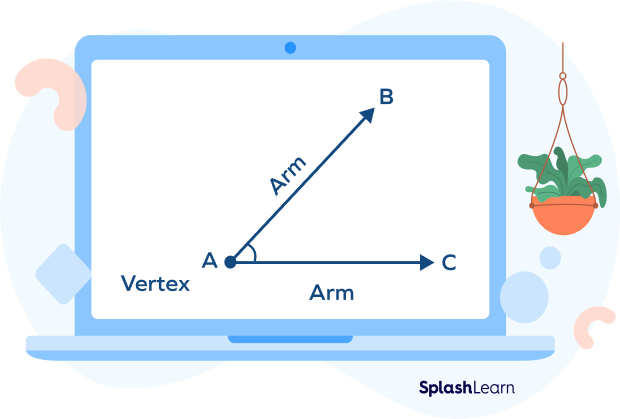
An angle is measured in° or radians. If the two arms of an angle extend in exactly opposite directions, it is a straight angle. A straight angle measures 180°. An angle can be measured using a protractor, and the angle of measure at 90 degrees is called a right angle. At a right angle, the two arms are perpendicular to each other.
Recommended Games
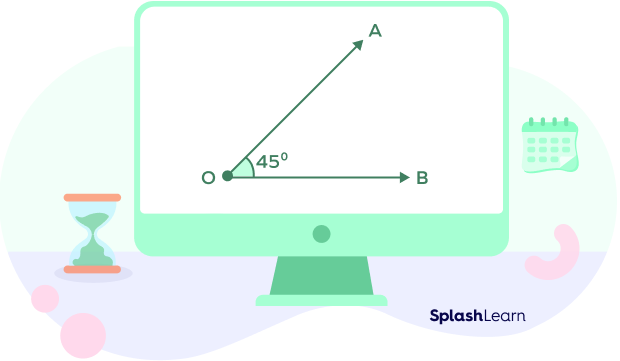
What is a 45-Degree Angle?
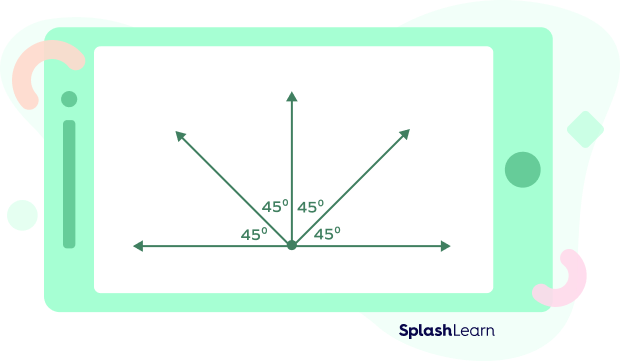
When the right angle is divided into two equal parts each angle measures 45°.

A 45-degree angle is an acute angle. It is half of the right angle or a 90-degree angle. Take a look at the image of the 45-degree angle.
Recommended Worksheets
Real-Life Examples of 45-degree Angle
We can see the 45-degree angle in a variety of places around us. For example, if the laptop screen is bent properly, it will form a 45-degree angle with the keyboard.
Similarly, if a door is opened halfway, it will form a 45-degree angle with the wall.
Consider the following examples of 45-degree angles found in our environment:
- A 45-degree angle allows the sun’s rays to travel the greatest distance. That is why some solar panels are angled at 45 degrees, depending on their geographical location.
- When throwing a ball, the 45-degree angle is optimal because it reaches the farthest.
- In architecture, the 45-degree angle is used to create designer doors and window grills.
Fun Facts About the 45-degree Angle
- A square’s diagonals form a 45-degree angle with its sides.
- An isosceles right triangle will have one right angle and two 45 degrees angles.
Construction of 45° Angle:
- a) Using a Protractor
The steps in forming a 45-degree angle are as follows:
Step 1: Draw a ray and name it AB.
Step 2: Keep the center point of the protractor at A. Since the angle opens to the right, choose 45° in the list that starts at the right and moves in the anticlockwise direction. Mark the point C.
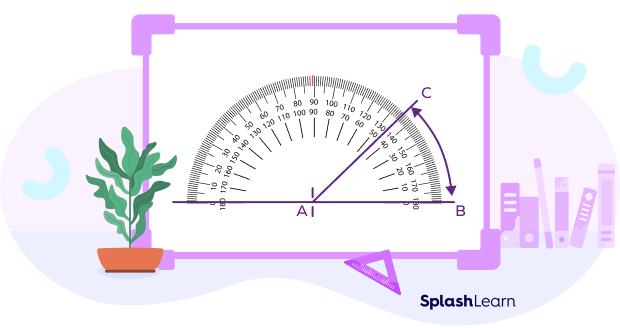
Step 3: Join A and C. Here are the measures.
a) Using a Compass
The steps in forming a 45-degree angle are as follows:
Step 1: Mark point A to create a 45° angle.
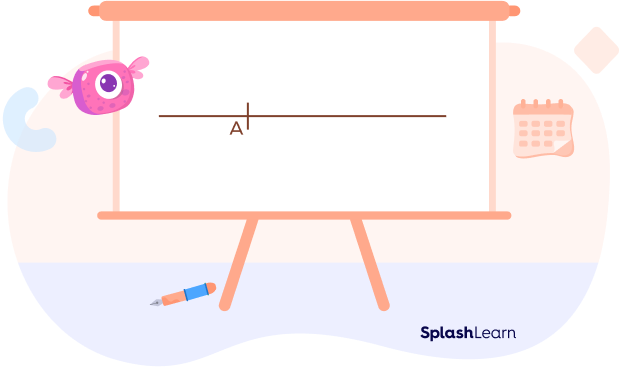
Step 2: Create a 90° angle first. Extend your compass beyond half the length of AB. Mark an arc above and below line segment AB with the sharp end.
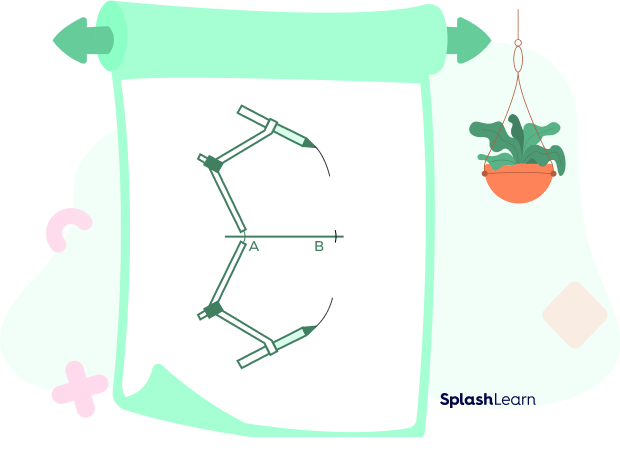
Step 3: Keeping the compass at its original width, place the sharp end at B and draw arcs above and below line segment AB to intersect with the arcs drawn in step 2.
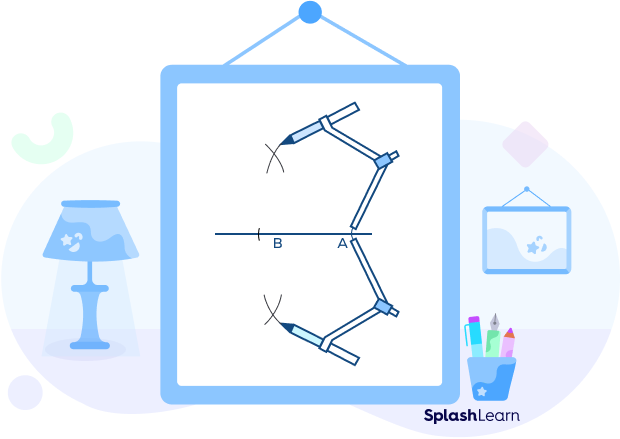
Step 4: Draw a straight line connecting the two points where the arcs intersect. This line bisects AB perpendicularly. P is AB’s midpoint.
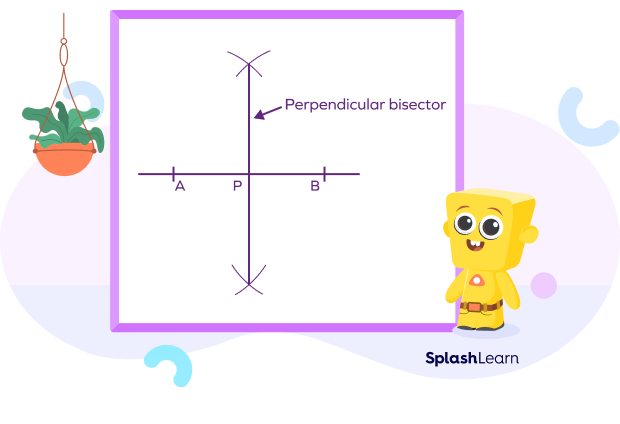
Step 5: Bisect the 90-degree angle in half to create a 45-degree angle.
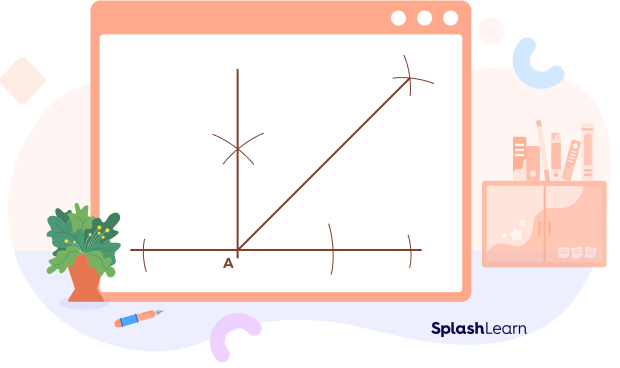
In summary, the steps involved in constructing a 45° angle are as follows:
- Create perpendicular lines to make a 90° angle.
- Divide the 90° angle in half to obtain a 45° angle.
Solved Examples on 45-Degree Angle
Example 1: What is the measurement of one-fourth of a 180° angle?
Solution:
One-fourth of 180° angle = 180/4 = 45
One-fourth of a 180° angle is a 45° angle.
Example 2: Tim drew a horizontal line on a piece of paper. By drawing a vertical line, Ron divided it in half. Upon his arrival, Jack further divided the two halves into four equal halves.
How many 45-degree angles are drawn on the paper?
Solution:
By drawing a vertical line on a horizontal line, Tim made two 90° angles.
Splitting each 90° angle in half yields two 45° angles.
So in all, there are four 45° angles..
Practice Problems on 45-Degree Angle
45 Degree Angle
A 45-degree angle is an example of what type of angle?
Angles smaller than 90-degree are acute angles.
Which of the following measures is not a right angle?
(2 X 90) degree gives 180 degrees, which forms a straight line.
An obtuse angle is _____ than a right angle.
Angles greater than 90 degrees are obtuse angles.
Two right angles make a _____ angle.
Two right angles make a 180-degree angle which gives a straight line.
The time on an analog clock when the hour and minute hand make an angle that is more than a right angle is
The time on an analog clock when the hour and minute hand make an angle that is more than a right angle among the given options is 5 pm.
Conclusion
We hope that with this lesson, we have tried to cover some basic definitions, the geometry of the 45-degree Angle, and real-life examples, which should give you at least a basic idea of what a 45-degree angle is. With the help of SplashLearn, you can learn how to learn better. You can download the SplashLearn App today, which will help you clear your doubts. Once you install the app, you can clear all your doubts on 45-degree Angle, trigonometry, and more such topics on your phone.
Frequently Asked Questions on 45-Degree Angle
What is a 45-degree angle?
45-degree angle is an acute angle measuring 45 degrees.
When an angle bisector is drawn for a 90-degree angle, the resulting smaller angles are 45 degrees each.
How do you form a 45-degree angle?
You can draw two perpendicular lines on a piece of paper. Then, divide the resulting right angle into two equal parts. Each equal part gives a 45-degree angle.
How can you form a 45-degree angle with the corner of a rectangle?
Place your protractor along any vertex of the rectangle and mark a point at 45 degrees. Now, remove the protractor and join the vertex with the point with a ruler.
What are the uses of a 45-degree angle in real life?
A 45-degree angle allows the sun’s rays to travel the greatest distance. That is why some solar panels are angled at 45 degrees, depending on their geographical location.
When throwing a ball, the 45-degree angle is optimal because it reaches the farthest.






























