What Is a Curved Line?
A curved line, as the name suggests, is a line that is bent. We see curved objects all around us. Curved lines are also known as bent lines. Note that a line is strictly straight. A curve can be considered as a generalization of a line.
You can observe that the letters A, I, T, etc., do not have any curved lines. However, we cannot write the letters like B, C, D, etc., without a curved line. What are some other day-to-day observations where you see curved lines? A mustache, a curved line over a series of notes in sheet music, a rainbow, a curved road, curly hair!

Recommended Games
Curved Line: Definition
A curved line is a type of line that is not straight and is bent. It is continuous and smooth, without any sharp turns.
We know that the curvature of the straight line is zero. Hence, when the curvature of a line is not zero, then we call it a curved line.

Imagine a bug has to move from point A to point B. What are the different ways in which the bug can reach from point A to point B?
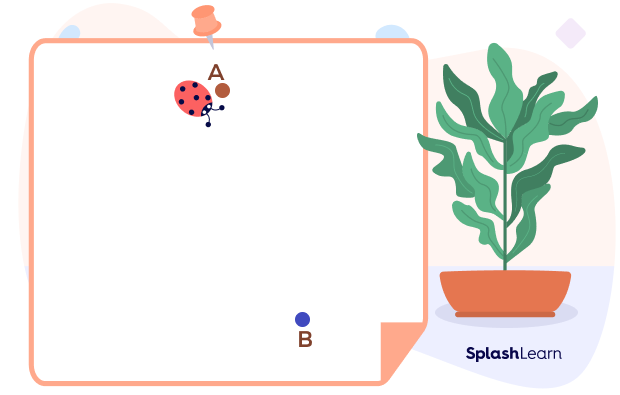
The bug can take several paths to reach from point A to B. The given figures show some of the paths that the ant can take to reach from point A to point B.
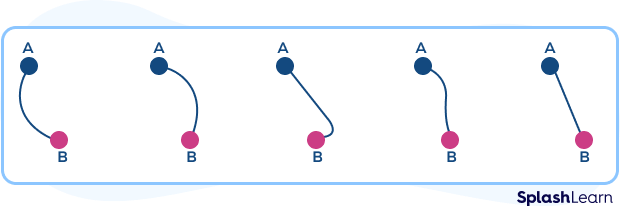
We see that in the first four figures, the ant changed its direction while traveling from point A to point B, that is, it did not follow one constant direction. However, in the last figure, the ant moved straight, and the distance it moved was the shortest. The movement from one point to another gives rise to straight or curved lines.
Recommended Worksheets
Examples of the Curved Line
The above letters and numbers are made of only curves.

Straight Lines vs. Curved Lines
Let us look at the difference between curved and straight lines.
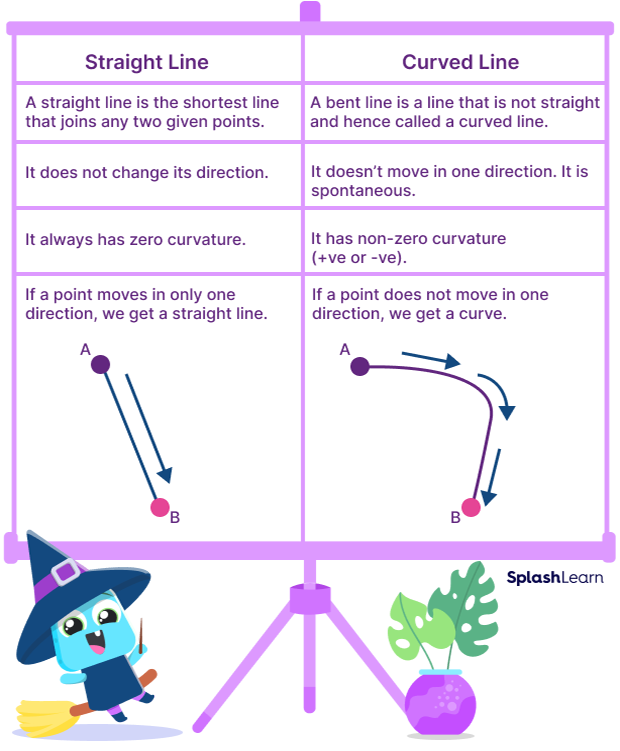
What Makes a Straight Line Different from a Curved Line?
Certain factors, such as curvature, random bending, and direction, make a straight line different from a curved line. All these different types of curves on a graph are also referenced.
Different Types of Curved Lines
Let’s discuss some types of curves formed by curved lines.
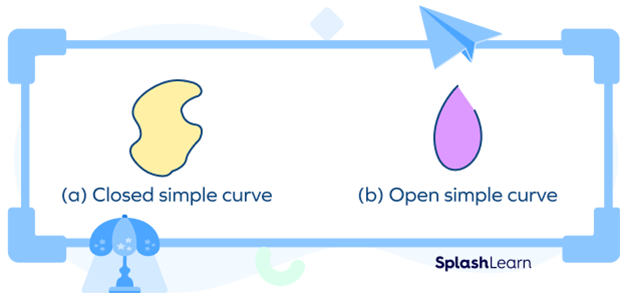
Open Curve
An open curve does not enclose any area within itself and has two endpoints. The examples of open curves are:

Closed Curve
A closed curve has no endpoints and encloses an area (or a region). It is formed by joining the endpoints of an open curve together. Circles and ellipses are formed using closed curves. A circle is a closed curve formed when a point moves in a plane such that it is at a constant distance from its center.
The examples of closed curves are:
Simple Curve
A simple curve is defined as a curve which doesn’t cut or cross itself. A simple curve changes direction but does not cross itself while changing direction. It can be open and closed.
Non-simple Curve
A curve that crosses its own path is called a non-simple curve.
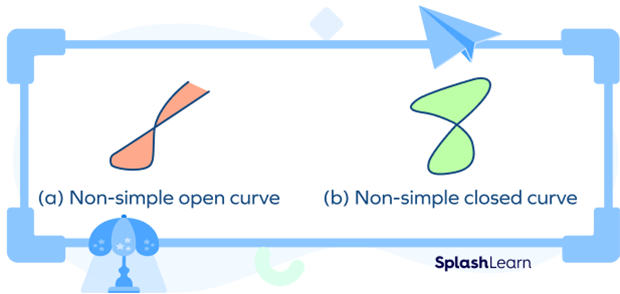
Fun Facts on Curved Lines
- Geometry is a branch of mathematics that deals with different figures and solids made up of straight and curved lines.
- We often see red curved underlines in word documents to indicate that there’s a grammatical error or spelling mistake. Have you observed? Check it out!
- Curved line equations: There is no specific formula for a curved line. For example, the equation $ax^{2} + by^{2} = c$ is the general equation for an ellipse. Here are a few general equations that graph curved lines.
- $\text{y} = \text{ax}^{n} ; a \gt 0, n =$ even
- $\text{y} = \text{ax}^{n} ; a \lt 0, n =$ even
- $\text{y} = \text{ax}^{n} ; a \gt 0, n =$ odd
- $\text{y} = \text{ax}^{n} ; a \lt 0, n =$ odd
- $\text{x} = \text{ay}^{n} ; a \lt 0, n =$ even
- $\text{x} = \text{ay}^{n} ; a \gt 0, n =$ even
- $\text{x} = \text{ay}^{n} ; a \lt 0, n =$ odd
- $\text{x} = \text{ay}^{n} ; a \gt 0, n =$ odd
- $f(\text{x}) = \text{ax}^{n} + \text{bx} + c; a \neq 0$
Conclusion
In this article, we learnt about Curved lines, commonly known as curves. We saw the different types of curves. Let’s solve some problems for better understanding.
Solved Examples on Curved Lines
1. Identify the open and closed curves from the below figure.
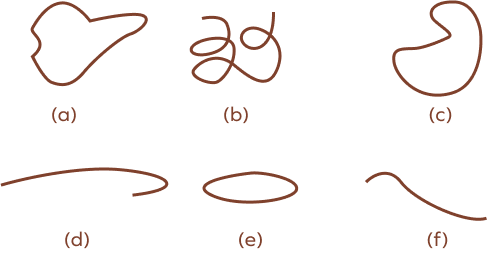
Solution:
As we can observe, the open curves are (b), (d), and (f).
The closed curves are the ones where the endpoints are joined together, (a), ©, and (e).
2. Which of the following letters represent open curves?
O, U, C, D, S
Alt tags: Curved lines in alphabets
Solution:
The letters representing open curves are U, C, and S. They all have two endpoints. However, the letters O and D are closed curves.
3. Identify the simple and non-simple curves.
8, Q, &, c, o
Alt tags: curved lines
Solution:
Simple curves: Curves that do not intersect when changing the direction. i.e., c, o
Non-simple curves: Curves that cross their own path, i.e., 8, Q, &
4. Identify the type of curve in the given picture.

Solution:
The curve in the given picture is an open curve.
Practice Problems
Curved Line – Definition with Examples
The letter O is an example of _______ .
It is a simple closed curve because it does not cross itself and its ends meet to enclose space.
Identify the type of curve in the given picture:

The curve in the given picture is a non-simple curve since it crosses its own path.
Which of the following is an open curve?
A circle and ellipse are closed curves. Parabola, however, is an open curve.
Identify the type of curve in the given picture:

The curve in the given picture is a non-simple curve.
Identify the type of curve in the given picture:

The curve in the given picture is an open curve.
Frequently Asked Questions
Define a straight line.
A straight line can be defined as a line traced by a point traveling in a constant direction.
What is the curvature of a line?
The curvature measures how fast a curve is changing direction at a given point.
What is the use of curved lines?
Curved lines are used commonly in the graphical representation of different types of functions.
What are a few English alphabets that are curved?
A few English alphabets which are curved are C, S, O, etc.
What is the highest or lowest part of a curve called?
The point where a curve is at its highest or lowest is called a vertex.