What is a Pentagon?
A 2D polygon with five sides and five angles is called a pentagon.
“Penta” means “five”, and “gon” translates to “angles” in Greek, and hence when we combine both words “penta + gon”, we get the word “pentagon”.
Recommended Games
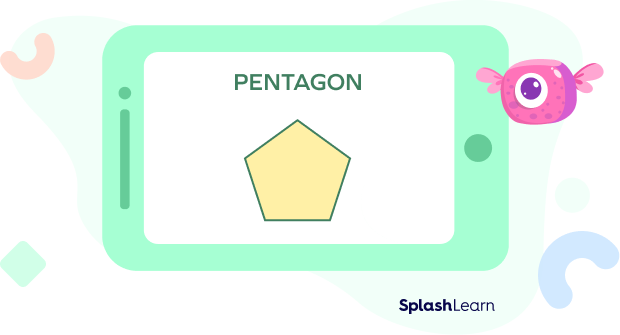
What does a Pentagon look like?
This is how the five sided shape looks like:
Recommended Worksheets
Parts of a Pentagon Shape
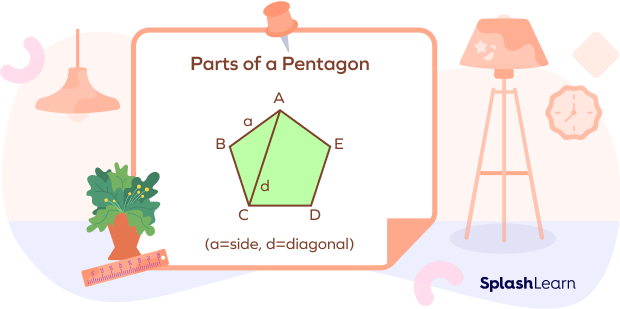
- Side: It is one of the five line segments that form this shape. There are a total of five sides in this shape. In the image, line segment ‘a’ shows one of the 5 pentagon shape sides.
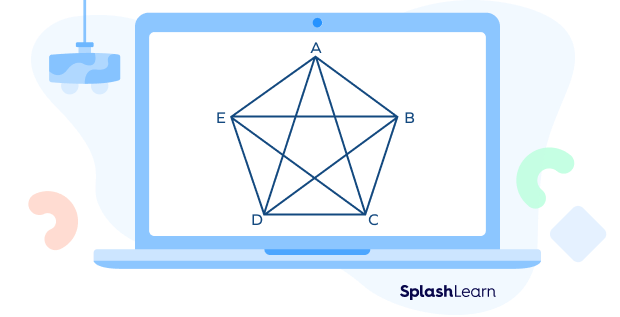
- Vertex: It is the point where two sides of the shape meet. In simpler terms, it is also known as a corner. For example, when you look at the page of your notebook, you will find that it has four corners or four vertices that form a 90° angle. In the above image, A,B,C D and E are the five vertices of this shape.
- Diagonal: It is a line that connects two non-adjacent vertices. When you connect any two non-adjacent corners or vertices of a 2D figure using a straight line, that straight line is known as the diagonal. The diagonal is represented with the letter “d” in the image for reference.
- Interior angle: It refers to the angle formed by two adjacent sides of the shape on the inside. When two straight lines meet or intersect, they form two types of angles in a closed 2D figure. The angle that lies within the figure is called an internal angle. Angles marked in green in the below image show interior angles.
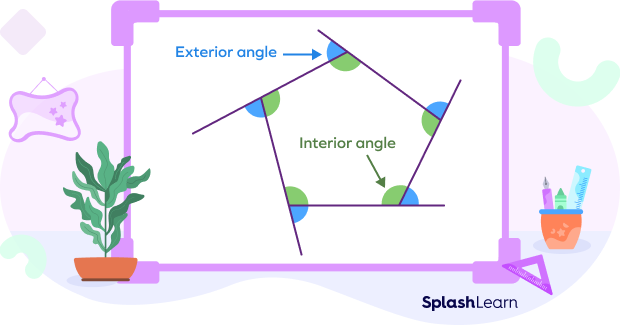
- Exterior angle: It refers to the angle formed by two adjacent sides of the shape on the outside. The external angle is the measure of the angle on a particular vertex but on the outside. Angles marked in blue in the above image show exterior angles.
Types of Pentagon
Pentagons can be classified into four types depending on their sides, angles, and vertices.
- Regular
- Irregular
- Convex
- Concave
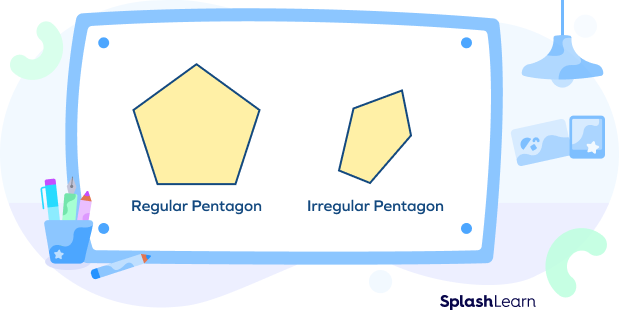
Regular and irregular pentagons
If all five sides are equal in length and all five angles have an equal measure, then the shape is called regular. When the side and angles are not equal, it is called irregular. To understand it better, if you look at a regular pentagon from any side, it will always look the same since it is symmetric. But, an irregular one might look different from all sides or angles since it has different side lengths and angles.
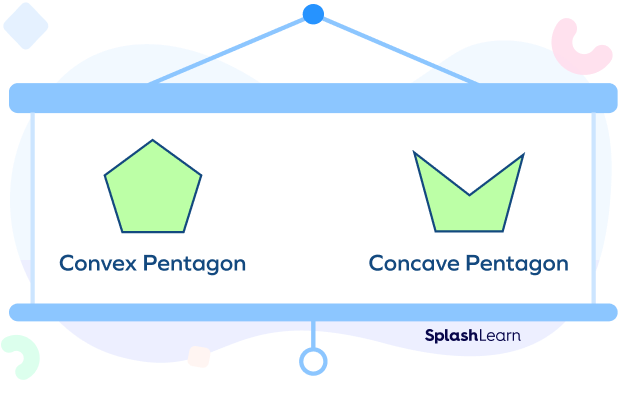
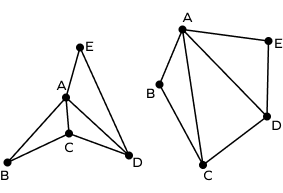
Convex and concave pentagons
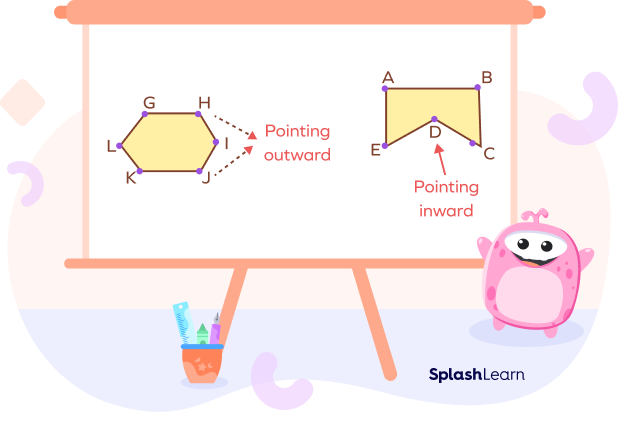
A convex pentagon is one in which all its vertices point outwards. A concave shape refers to the one with at least one vertex pointing inward.
In other words, a concave pentagon will have a bowl-like shape between some sides, while a convex will not have such a shape, as all of its vertices point outwards.
Properties of a Pentagon
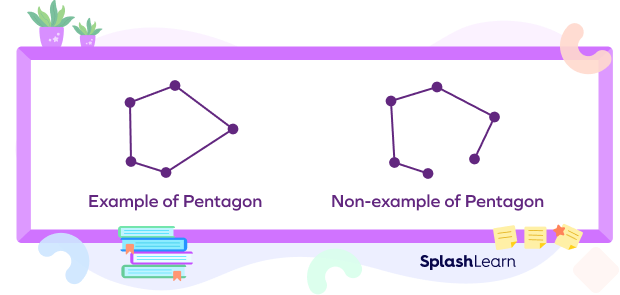
- This shape must have five sides that form a closed 2D figure. (A closed figure is one in which all of its sides meet with each other to form vertices.)
- A pentagon shape has five diagonals connecting the five vertices to their opposite vertices.
- In a regular pentagon, each interior angle measures 108°, and each exterior angle measures 72°.
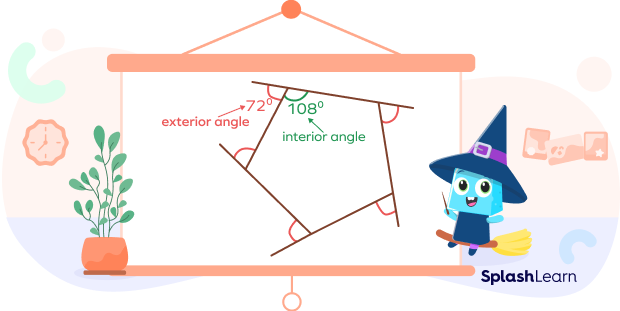
- The sum of all the five interior angles in any pentagon is 540°.
Pentagon Examples in Real-life
- Football: A football is made up of several black and white patches of this five-sided shape.
- Okra: The next time you eat okra, look at the interior cross-section closely as it has a pentagonal shape.
- Pentagon building: The U.S. Dept. of Defense headquarters in Washington, DC, is a pentagonal-shaped building named The Pentagon.

Area of a Pentagon
The area of this shape is the total space within its five sides. To find the area, we must first determine its type and the information we have about it.
Area of Regular Pentagon:
A regular one forms five similar triangles.
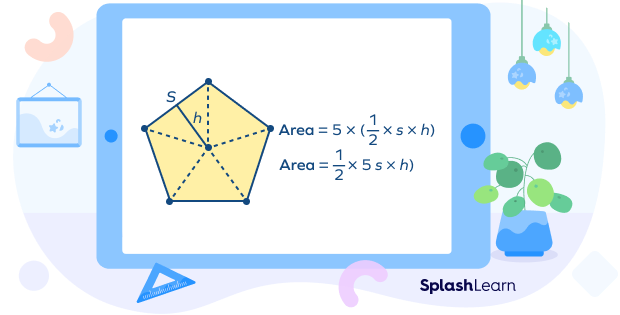
Area of regular pentagon = 5 × Area of the triangle or
= 1/2 × Perimeter × Apothem sq units
Apothem is a perpendicular line from the center of a polygon to one of its sides. It is also known as the radius of the shape.
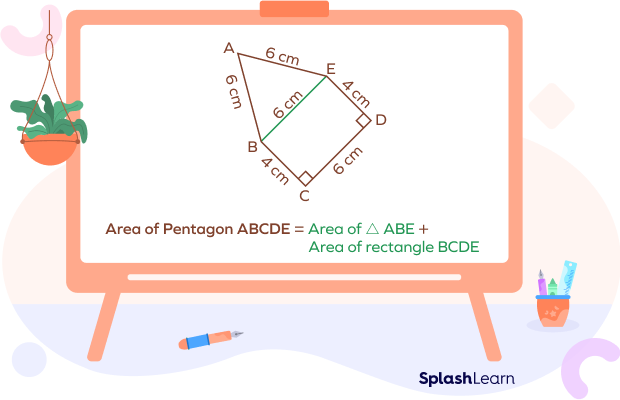
Area of Irregular Pentagon
To find the area of an irregular pentagon, divide it into smaller polygons. The sum total of all the areas of the smaller polygons gives the total area of the shape.
The Perimeter of a Pentagon
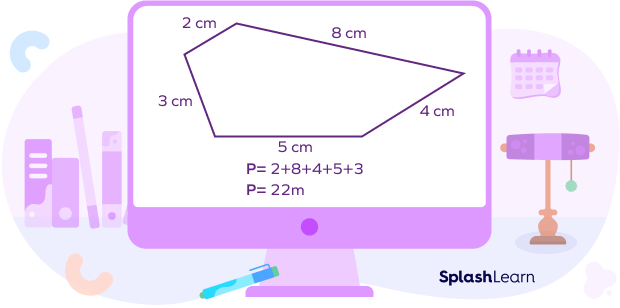
The total length of the five sides of a regular or irregular polygon is called its perimeter.
Perimeter of a pentagon = (side 1 + side 2 + side 3 + side 4 + side 5) units
The perimeter of a regular five sided shape equals (5 x side) units if all the sides have the same measurement.
Fun Facts
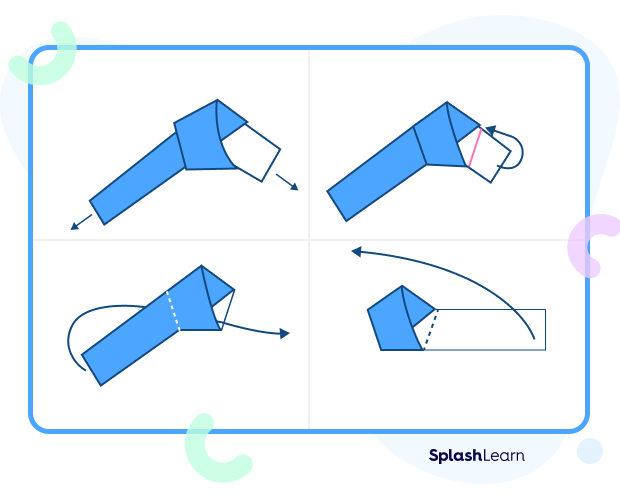
Did you know you can create a simple paper strip pentagon?
Step 01: Get a long paper strip. You can choose your favorite color.
Step 02: Now, make a pretzel-like knot with the paper. Look at the image and follow the instructions.
Step 03: While keeping the paper flat, tighten the knot with soft hands. Be careful not to tear it.
Step 04: Now, if there is excess paper, fold it back or trim it off.
Step 05: Voila! It is now ready. You can check if all sides are of the same length and all the angles are of the same measure.
Conclusion
Pentagons are extensively used by architects and are found throughout the natural world. They are also very commonly used in fundamental geometry. To learn geometry principles in a fun and engaging way, check out SplashLearn‘s educational games, courses, and worksheets for kids.
Solved Examples
- Neal measures a regular pentagon and finds that its side is 8 feet and the apothem is 6 feet long. How will he find its area?
Solution:
Given in question,
Apothem = 6 feet
Side = 8 feet
Area of Regular Pentagon = ½ × perimeter × apothem
= ½ × 5 × 8 × 6
= ½ × 240
= 120 sq feet
Therefore, the area = 120 feet2
- If a regular pentagon has the side length of 10 cm and an apothem of 5 cm, find its area.
Solution: Given,
Length of side = 10 cm
Length of apothem = 5 cm
Area of Regular Pentagon = ½ × perimeter × apothem
= 1⁄2 × 5 x 10 × 5
Area = 125 cm2
- If the perimeter of a regular pentagon is 200 cm, what would be the length of each side?
Solution:
Perimeter of regular pentagon = 200 cm
5 × side= 200
Side = 200/5
Side = 40 cm
The length of each side is 40 cm.
Practice Problems
What is a Pentagon? - Definition, Types, Properties & Examples
How many parallel sides can there be in a regular pentagon?
A regular pentagon has zero parallel sides. An irregular one can have two (one pair) or four (two pairs) parallel sides.
The side length of a perimeter is 6 cm. What is the perimeter of the pentagon?
Perimeter of a pentagon = side length of the pentagon x 5
The given side length is 6 cm.
If the perimeter of a regular pentagon measures 250 cm, what would be the measure of each side?
Perimeter of regular pentagon = 250 cm
5 × side= 250
Side = 250/5
Side = 50 cm
How many triangles can a pentagon be divided into?
A pentagon can be divided into 3 triangles.
If the measure of an irregular pentagon’s four interior angles is 135, 78, 119, and 117°, what would be the measure of its fifth interior angle?
Sum of all interior angles of a pentagon is 540°.
Hence $135 + 78 + 119 + 117 + X$ = $540$ (X is the unknown angle)
$X$ = $540$ – $449$ = $91°$
What is the area of the pentagon whose side measures 9 cm and apothem measures 10 cm?
Perimeter of a pentagon = side length x 5
Perimeter = 9 x 5 = 45 cm
Area of pentagon = 1/2 × p × a
Area = ½ x 45 x 10
Area = 225 cm²
Frequently Asked Questions
Is a pentagon also a parallelogram?
No, a pentagon is a five-sided polygon, while there are only four sides in a parallelogram.
How are a quadrilateral and a pentagon similar?
A. A quadrilateral and a pentagon are closed polygons with the sum of their exterior angles as 360°.
What are the three attributes of a regular pentagon?
- All five sides must be congruent (of equal length).
- All five interior angles must measure 108° each.
- All five exterior angles must measure 72° each.
How many right angles can a pentagon have?
A pentagon can have a maximum of three right angles. If the number of right angles is four, the last angle will have to measure 180° for the sum of all interior angles to be 540°, which is not possible.
How many acute and obtuse angles does a regular pentagon have?
A pentagon has zero acute angles and five obtuse angles, each measuring 108°.
Can a pentagon have five unequal sides?
Yes, all sides and angles of an unequal pentagon can be different from each other.



















