Let us look at the following pictures.

Can you guess its shape?
This is shaped like a pentagonal prism.
What is a Pentagonal Prism?
A pentagonal prism or five-sided polygonal prism is a prism that consists of two pentagonal bases (the top and the bottom) and five rectangular sides.
Pentagonal Prism is a heptahedron that consists of:
- Five rectangular sides
- 15 edges
- Ten vertices
- Seven Faces
It is easier to understand how a usual pentagonal prism looks by going through the image below.
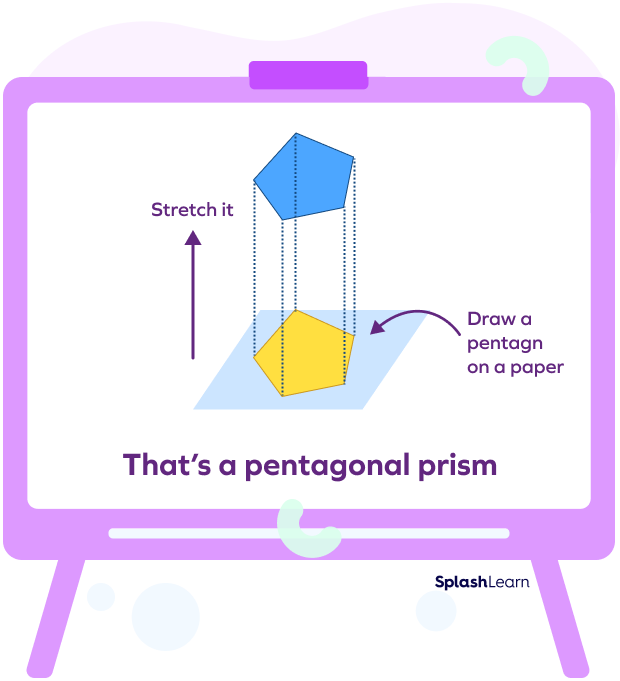
In this image, we can see that if we draw two pentagons (one on the top and the other on the bottom) and then connect them through straight lines, we will get a pentagonal prism.
You can find many real-life examples of pentagonal prisms.
- Pentagon – US Defence Department Headquarter

- Clocks

- Barns

- Nuts
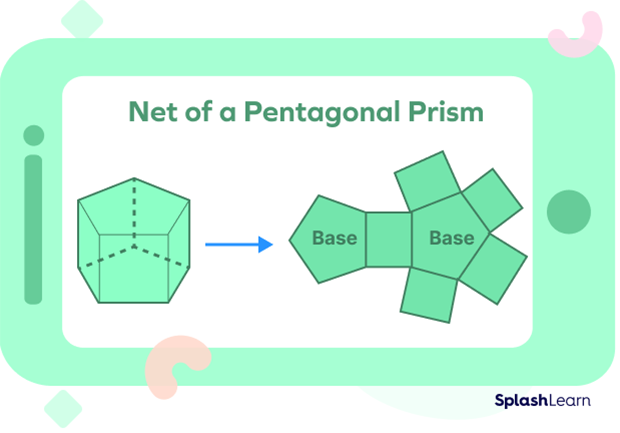
Net of a Pentagonal Prism
Surface Area of a Pentagonal Prism
A pentagonal prism has two types of surface areas: total surface area and lateral surface area.
Total Surface Area of a Pentagonal Prism
A regular pentagonal prism’s total surface area gives each face’s area (i.e., seven prism faces). Thus, the total surface area of the regular pentagonal prism is calculated as:
TSA $= 5ab + 5bh$ square units.
Here a is the apothem length (a line that connects the center of the regular polygon to the midpoint of one of the sides of the polygon) of the pentagonal base, b is the side length of the base, and h is the height of a pentagonal prism.
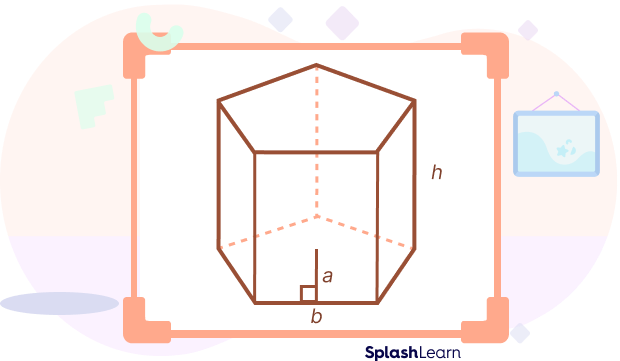
Lateral Surface Area of a Pentagonal Prism
One can also calculate the lateral or curved surface area of a regular pentagonal prism using the formula below:
LSA $= 5bh$, where b is the side length of the base, and h is the height of the pentagonal prism
The Volume of a Pentagonal Prism
The volume of a pentagonal prism represents the space occupied by that prism. So, we can obtain the value of the pentagonal prism using a simple formula.
$V =$ area of base$\times$height.
However, to use the above formula, we need to know the area of the base of a pentagonal prism. Thus, to calculate the area of the base of a regular prism, the following formula is applied:
Area of base $= 1/2$$ \times$ perimeter $\times$ apothem length or $1/2$$ \times$$ 5bh$
In other words, the volume of a regular pentagonal prism can also be calculated using the following formula.
$V = (5/2)$$\times a \times b \times h$
Solved Examples
Q1. The perimeter of a pentagonal prism is 150 inches, and its height is 55 inches. Calculate its lateral surface area.
Solution:
The perimeter of a pentagonal prism is 150 inches (given).
Therefore, $P = 150$ inches
The height of a pentagonal prism is 55 inches (given).
Therefore, $h = 55$ inches.
Thus, the lateral Surface area or LSA $= Ph = (150) \times (55) = 8,250$ sq. inches
Q2. If the apothem length, base side, and height of a regular pentagonal prism are 5 inches, 8 inches, and 10 inches, respectively. Find the total surface area of the prism.
Solution:
The apothem length of the pentagonal prism is 5 inches (given).
Therefore, $a = 5$ inches.
The base length of the pentagonal prism is 8 inches (given).
Therefore, $b = 8$ inches.
The height of the pentagonal prism is 10 inches (given).
Therefore, $h = 10$ inches.
Plugging the values in the formula for the surface area of a regular pentagonal prism, we get
TSA $= 5ab + 5bh$
$= (5 \times 5 \times 8) + (5 \times 8 \times 10)$
Thus, the total surface area of the prism is 600 cubic inches.
Q3. Find the volume of a chocolate box shaped as a regular pentagonal prism whose apothem length is 10 cm, base length is 20 cm, and height is 15 cm.
Solution:
To calculate the volume of a regular pentagonal prism, we use the formula below:
$V = 5/2$$ \times a \times b \times h$
Plugging the values in the formula for the surface area of a regular pentagonal prism, we get
$V = 5/2$$ \times 10 \times 20 \times 15 = 7500$ cubic cm
Thus, the volume of the chocolate box is 7500 cubic cm.
Practice Problems
Pentagonal Prism - Definition with Examples
Identify the type of pentagonal prism below:

It is a Right Pentagonal Prism because it has two congruent and parallel pentagonal faces.
If the apothem length (radius of the inscribed circle in a regular polygon) of a pentagonal prism is doubled, its total surface area will:
In the above formula of the total surface area (TSA) of a regular pentagonal prism, we learned that
TSA $= 5ab + 5bh$. This means that if the apothem length will double, its total surface area
will increase, but not double.
Suppose the base length of a regular pentagonal prism is doubled, what will happen to its lateral surface area?
We have learned that the lateral surface area of a regular pentagonal prism is $5bh$. So, if the height of the pentagonal prism doubles, we can conclude that its lateral surface area will also be doubled.
Frequently Asked Questions
What is a prism?
Any 3-D shape which has two parallel and congruent faces or bases is defined as a prism.
What do face and base mean in a pentagonal prism?
The faces of a pentagonal prism are the flat side of a 3-D object, whereas its base is defined as one of the two congruent sides of the prism.
What do you mean by the apothem length of a polygon?
Apothem length of a regular polygon is the line that connects the center of the regular polygon to the midpoint of one of the sides of the polygon. It is also used to find any regular polygon’s surface area and volume, including a pentagonal prism.