Scalene Triangle – Definition With Examples

Scalene Triangle – Introduction

A scalene triangle is a triangle whose all sides are unequal and all angles have different measures. We know that a triangle is a three-sided polygon that consists of three edges and three vertices. There are three types of triangle based on the length of its sides:

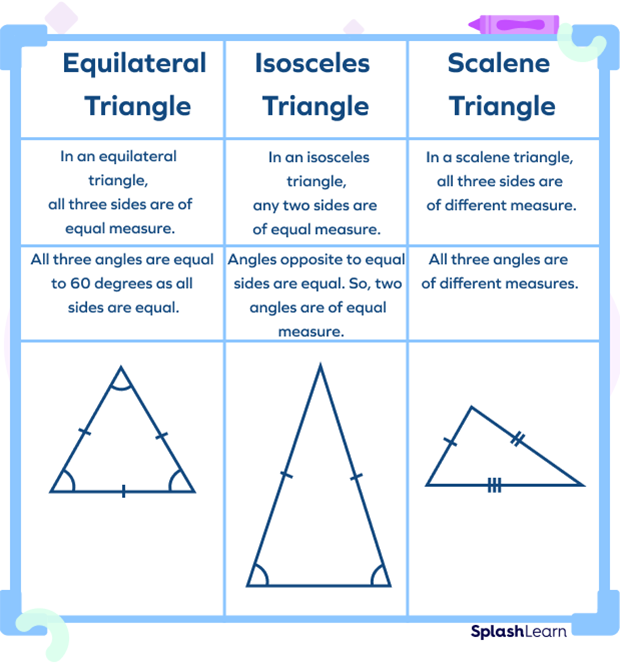
1. Equilateral triangle: All sides are equal in length.
2. Isosceles triangle: Two sides are equal in length.
3. Scalene triangle: All sides have different lengths.

What is A Scalene Triangle?

A scalene triangle is a triangle in which all the sides are of different lengths and all angles are of different measures. 

For example: 

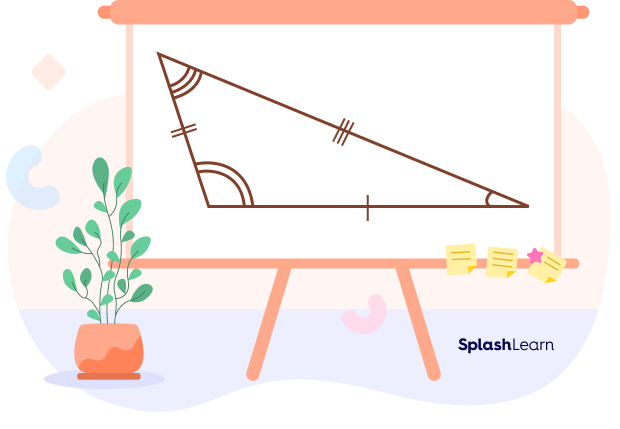
In the figure given above, all the three symbols that are given on each side are different, which denotes that all three sides are unequal. Also, all the three angles are of different measures. So, the triangle is scalene.

Definition of Scalene Triangle 

A scalene triangle can be defined as a triangle whose all three sides have different lengths, and all three angles are of different measures. The angles of a scalene triangle follow the angle sum property and always add up to 180. 

Types of Scalene Triangles

A scalene triangle can be classified into three categories:

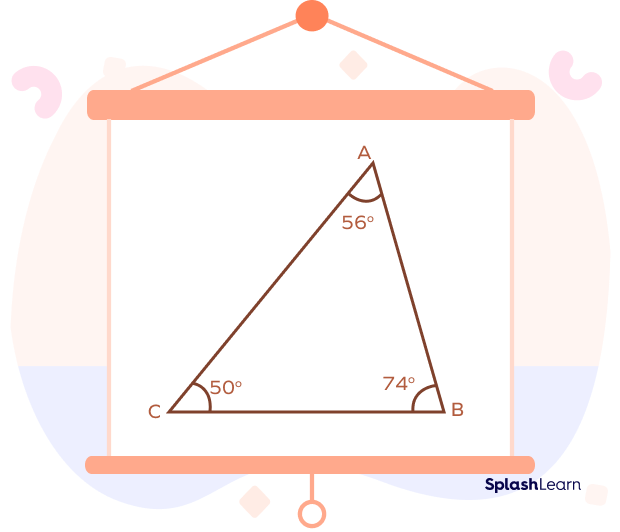
• Acute-angled scalene triangle 

In an acute-angled scalene triangle, each angle of the triangle is less than 90°. In simple words, all angles are acute angles. 

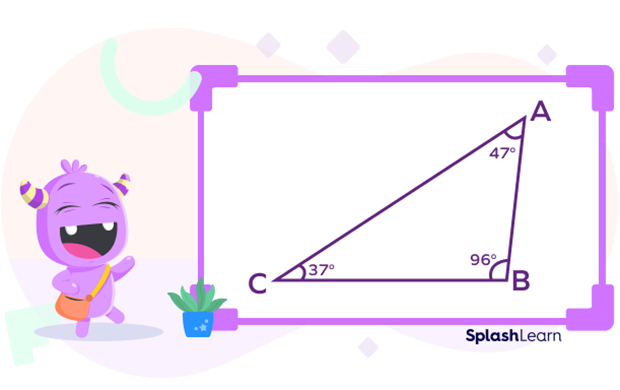
• Obtuse-angled scalene triangle 

In an obtuse angled scalene triangle, there is one obtuse angle (between 90° and 180°) and remaining two angles are acute.

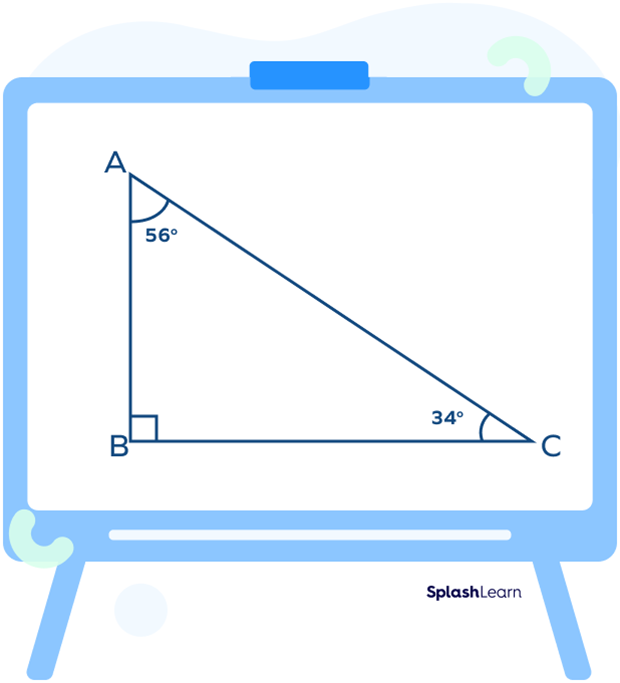
• Right-angled scalene triangle 

In a right-angled scalene triangle, one angle of the triangle is a right angle (one angle is equal to 90°).

Properties of A Scalene Triangle

• It has three sides of different lengths.
• It has three angles of different measurements.
• It has no equal or parallel sides. Hence, there is no line of symmetry in a scalene triangle.
• It has no point symmetry or rotational symmetry. 

Angle Sum Property of a Triangle

The sum of all three internal angles of a scalene triangle is 180°. It is also known as the angle sum property of the triangle. 

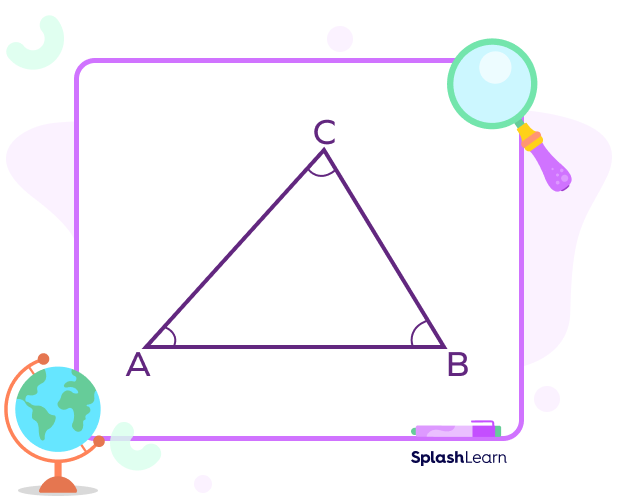
In $\Delta\text{ABC}, ∠\text{A} + ∠\text{B} + ∠\text{C} = 180°$

The difference in the sides or the angles do not affect the basic properties of a triangle.

For example: In $\Delta\text{PQR}, ∠\text{P} = 60°, ∠\text{Q} = 70°$

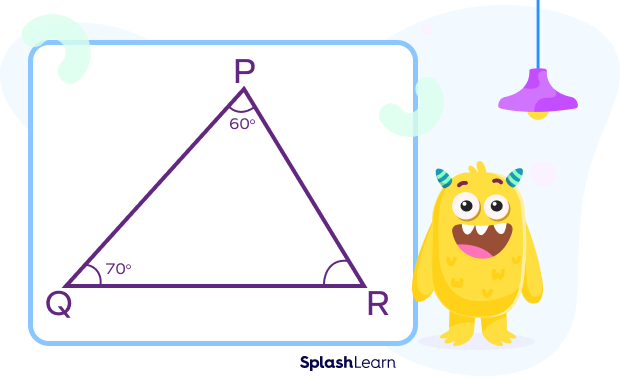
By the angle sum property of a triangle

$∠\text{P} + ∠\text{Q} + ∠\text{R} = 180°$

$60° + 70° + ∠\text{R} = 180°$

$130° + ∠\text{R} = 180°$

$∠\text{R} = 50°$

Area of a Scalene Triangle

Formula to calculate the area of a scalene triangle is the same as the formula to calculate the area of any other triangle.

1. When base and height are given

Area of a triangle $= \frac{1}{2}\times b\times h$ square units

Where, “b” refers to the base of the triangle, and

“h” refers to the height of the triangle. 

Example: Find the area of the given triangle.

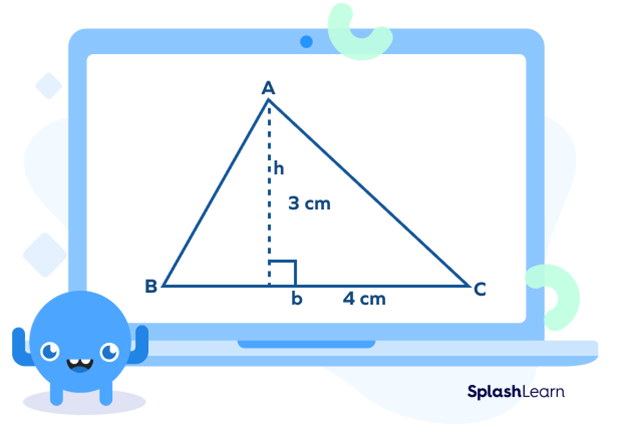
$b=4 \text{cm}$ and $h = 3\text {cm}$

Area of triangle $= \frac{1}{2}\times4\times3=6 \text{cm}^2$

2. When the sides of a triangle are given

When we don’t have the base and height for the scalene triangle and we have given the sides, then we apply Heron’s formula.

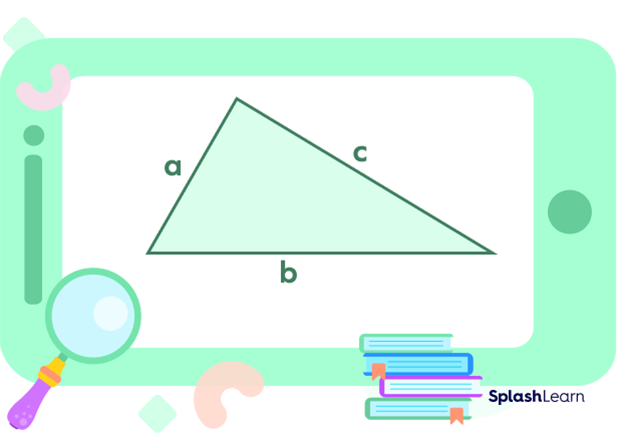
Area of the triangle $= \sqrt{s(s-a)(s-b)(s-c)}$ square units

Where, s is the semi perimeter of a triangle, therefore, 

$\text{s}=\frac{a+b+c}{2}$

Here, a, b, and c denote the sides of the triangle. 

Example: The sides of a triangle are 3 cm, 4cm and 5 cm. 

Let $a = 3 \text{cm}, b = 4 \text{cm}$ and $c = 5 \text{cm}$

$\text{s}= \frac{a+b+c}{2} = \frac{3+4+5}{2}=6$

Area $= \sqrt{6(6-3)(6-4)(6-5)}=\sqrt{6\times3\times2\times1}=6 \text{cm}^2$   

Equilateral Triangle v. Scalene Triangle v. Isosceles Triangle

Perimeter of a Scalene Triangle

The perimeter of any triangle = Sum of all the sides of a triangle. 

If the sides of a triangle are “a” units, “b” units and “c” units, then

Perimeter $= \text{a} + \text{b} + \text{c}$ units

Example: Consider a given triangle.

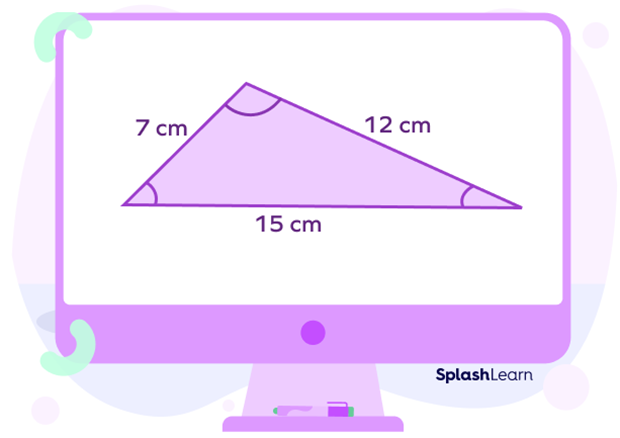
Perimeter of the triangle $= 7 + 12 + 15 = 34 \text{cm}$

Solved Examples

1. What will be the perimeter of the triangle with sides 10 cm, 12 cm, and 13 cm?

Solution: Perimeter = Sum of all the sides of a triangle $= 10 + 12 + 13 = 35 \text{cm}$

2. Find the area of the triangle with sides 20 cm, 21 cm, and 29 cm. 

Solution: Let $a = 20 \text{cm}, b = 21 \text{cm}$ and $c = 29 \text{cm}$

$\text{s}=\frac{20+21+29}{2}=\frac{70}{2}=35$

Area $= \sqrt{35(35 – 20)(35 – 21)(35 – 29)} = \sqrt{35\times15\times14\times6}=210 \text{cm}^2$

3. In PQR, $∠\text{P} = 30°, ∠\text{Q} = 60°$, find the value of $∠\text{R}$. Also, which type of a triangle is it called? 

Solution: In PQR, by angle sum property of a triangle,

$∠\text{P} + ∠\text{Q} + ∠\text{R} = 180°$

$30° + 60° + ∠\text{R} = 180°$

$∠\text{R} = 180° – 30° – 60° = 90°$

It is a right angled scalene triangle.

Practice Problems

Frequently Asked Questions