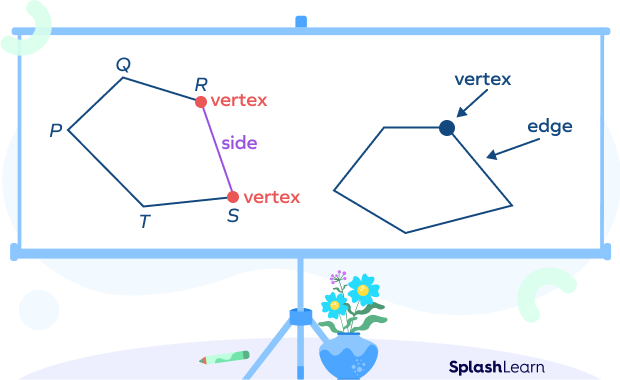
What Are Sides of a Polygon?
The sides of a polygon are the straight line segments that form the outer boundary of the polygon. Each side connects two consecutive vertices (corners) of the polygon.
The sides of a polygon are also called its edges. The points where two sides meet are the vertices (or corners) of a polygon.
Recommended Games
What Are Polygons?
In geometry, a polygon can be defined as a flat or two-dimensional closed shape bounded with straight sides. It does not have a curved boundary. At least 3 straight line segments (sides) are required to form a polygon.
Here are a few examples of polygons.
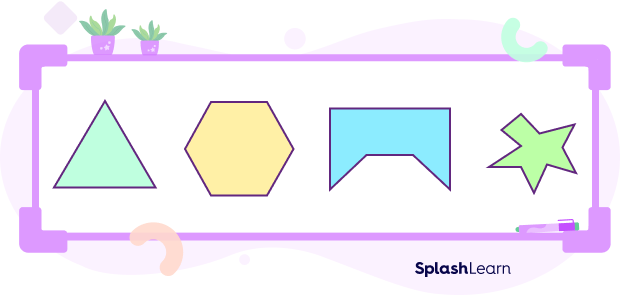
Here are a few non-examples of a polygon.
Recommended Worksheets
Sides of a Polygon: Definition
Sides of a polygon are the line segments that define the boundary of the polygon.
Classification of Polygons Based on the Number of Sides
We can classify polygons based on the number of sides. The minimum number of sides required to make a polygon is 3.
| Polygon names and sides | |
| Number of sides | Name of the polygon |
| 3 | Triangle |
| 4 | Quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | Nonagon |
| 10 | Decagon |
| n | n – gon |
Types of Polygons Based on Sides
Let’s discuss types of polygons based on different criteria.
- Simple and Complex Polygons:
This classification is done depending whether the sides cross themselves or not.
| Simple Polygons | Complex Polygon |
|---|---|
| Simple polygons are the polygons whose sides do not cross each other. | Complex polygons, which are also known as self-intersecting polygons, contain sides that cross each other. |
 |  |
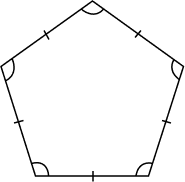
- Regular and Irregular Polygons
This classification is done on the basis of the measurements of sides and angles.
| Regular Polygons | Irregular Polygon |
|---|---|
| Polygons that have equal sides and equal interior angles are called regular polygons. | Polygons that are not regular (sides are not equal, or angles are not equal, both angles and sides are not equal ) are called irregular polygons. |
| Examples: Square, equilateral triangle | Examples: Rectangle |
 |  |
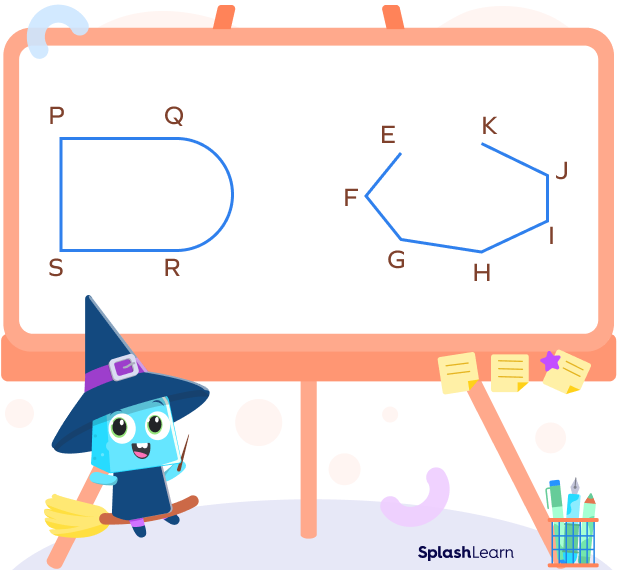
How to Find the Number of Sides of a Polygon
The number of sides in a polygon can vary, and different polygons have different shapes and side lengths. For example, a triangle has three sides, a quadrilateral has four sides, and a pentagon has five sides, etc.
- Number of sides of a polygon given the sum of interior angles
Sum of interior angles $= (n \;-\; 2) \times 180^{\circ}$
where
n is the number of sides.
Example: If the sum of interior angles of a polygon is 180, find the number of sides.
$180^{\circ} = (n – 2) \times 180^{\circ}$
$\Rightarrow 1 = n – 2$
$\Rightarrow n = 3$
- Number of sides of a “regular polygon” given the measure of an interior angle
Each interior angle of a regular polygon $= \frac{(n – 2) \times 180^{\circ}}{n}$,
where
n is the number of sides.
Example: If each interior angle of a polygon is 90, find the number of sides.
$\Rightarrow 90^{\circ} = \frac{(n – 2) \times 180^{\circ}}{n}$
$\Rightarrow \frac{90^{\circ}}{180^{\circ}} \times n = n – 2$
$\Rightarrow \frac{n}{2} = n – 2$
$\Rightarrow n – \frac{n}{2} = 2$
$\Rightarrow \frac{n}{2} = 2$
$\Rightarrow n = 4$
- Number of sides of a regular polygon when given the measure of an exterior angle
To find the number of sides of a polygon when the exterior angle is given, we use the formula:
Measure of an exterior angle of a regular polygon $= \frac{360^{\circ}}{n}$
where
n is the number of sides.
Example: If each exterior angle of a polygon is 36, find the number of sides.
$36^{\circ} = \frac{360^{\circ}}{n}$
$\Rightarrow n = 10$
Facts about Sides of a Polygon
- The number of interior angles of a polygon are equal to the number of sides present.
- Diagonals of a polygon are line segments that connect two non-adjacent vertices.
Conclusion
In this article, we learned about the sides in a polygon, an essential part of a polygon. Sides of a polygon are the line segments that form the boundary. Let’s solve a few examples and practice MCQs for better comprehension.
Solved Examples on Sides of a Polygon
1. How many sides are there in the following figure?
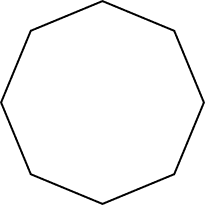
Solution:
The number of sides in the above polygon are 8.
Let’s name the vertices.
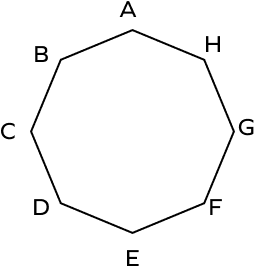
The 8 sides are:
AB, BC, CD, DE, EF, FG, GH, and AH.
2. Find the number of sides when the sum of interior angles of a polygon is $1080^{\circ}$.
Solution:
Sum of interior angles of a polygon $= (n – 2) \times 180^{\circ}$
where
‘n’ is the number of sides
Thus, $1080^{\circ} = (n – 2) \times 180^{\circ}$
$n – 2 = \frac{1080^{\circ}}{180^{\circ}}$
$n – 2 = 6$
$n = 8$
3. Find the number of sides of a regular polygon when each interior angle is $60^{\circ}$.
Solution:
Each interior angle of a regular polygon $= \frac{(n – 2) \times 180^{\circ}}{n}$
$60^{\circ} = \frac{(n – 2) \times 180^{\circ}}{n}$
$\frac{60^{\circ}}{180^{\circ}} n = n – 2$
$\frac{n}{3} = n – 2$
$2 = n – \frac{n}{3}$
$2 = \frac{3n – n}{3}$
$2 = \frac{2n}{3}$
$n = 3$
4. Identify regular and irregular polygons: Square, Rhombus, Equilateral Triangle, Rectangle.
Solution:
Square and equilateral triangle are regular polygons.
Rectangle and rhombus are irregular polygons.
Rectangle has equal interior angles, but non-equal sides.
Rhombus has equal sides, but non-equal angles.
6. Find the number of sides of a polygon when the interior angle sum is $1440^{\circ}$.
Solution:
$1440^{\circ} = (n – 2) \times 180^{\circ}$
$n – 2 = \frac{1440^{\circ}}{180^{\circ}}$
$n – 2 = 8$
$n = 8 + 2 = 10$
7. Name a regular polygon whose each interior angle is $162^{\circ}$.
Solution:
Each interior angle of a regular polygon $= \frac{(n – 2) \times 180^{\circ}}{n}$, where “n” represents the number of sides.
$162^{\circ} = \frac{(n – 2) \times 180^{\circ}}{n}$
$\frac{162^{\circ}}{180^{\circ}} n = n – 2$
$\frac{9}{10}n = n – 2$
$2 = n – \frac{9n}{10}$
$2 = \frac{10n – 9n}{3}$
$2 = \frac{n}{10}$
$n = 20$
The polygon is a regular 20-gon (also called regular icosagon).
Practice Problems on Sides of a Polygon
How to Find Sides of a Polygon – Definition, Examples, Facts, FAQs
Which polygon has 6 sides?
A hexagon has 6 sides.
A polygon with 9 sides is called ____.
A nonagon has 9 sides.
The polygon with equal number of sides and angles is called
A regular polygon has an equal number of sides and angles.
A polygon whose sides cross each other is called
A complex polygon has self-intersecting sides.
The number of sides of a regular polygon when the exterior angle is $30^{\circ}$ is:
Each exterior angle $= 30^{\circ}$
Number of sides $= n = \frac{360^{\circ}}{30^{\circ}} = 12$
Which polygon has the sum of interior angles $= 540^{\circ}$?
Sum of angles $= 540^{\circ}$
$540^{\circ} = (n - 2) \times 180^{\circ}$
$n - 2 = \frac{540^{\circ}}{180^{\circ}}$
$n - 2 = 3$
$n = 3 + 2 = 5$
The polygon is pentagon.
Frequently Asked Questions about Sides of a Polygon
What is the difference between sides of a polygon and diagonals of a polygon?
The sides of a polygon are the line segments that make a polygon. On the other hand, diagonals are the line segments that join two non adjacent vertices of a polygon.
Can a polygon be formed with 2 sides?
A polygon is a closed figure with at least 3 sides.
What is the name of the polygon with 20 sides?
The polygon which has 20 sides is called Icosagon.
Is a circle a polygon?
A circle is not a polygon.





























