What Is a Hypotenuse?
A right-angled triangle is a triangle that has one interior angle, which measures 90 degrees. The side opposite to the right angle in a right-angled triangle is known as the hypotenuse. It is the longest side.
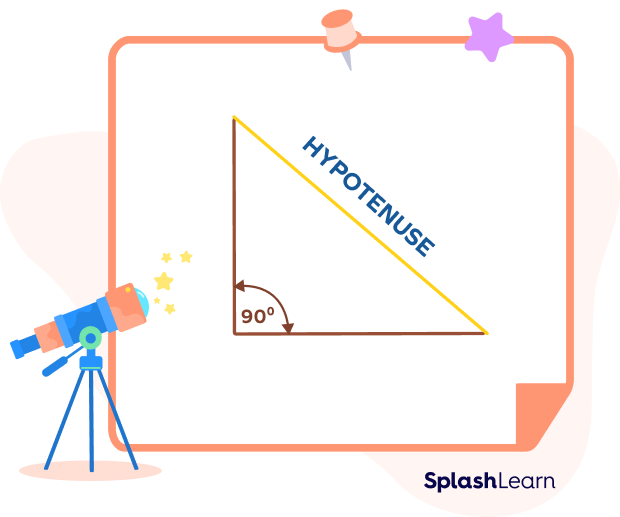
Definition of Hypotenuse?
The sides of a right triangle are base, perpendicular, and hypotenuse. As mentioned earlier, the hypotenuse of a right triangle lies opposite to the right angle. In a right-angled triangle, the sides other than the hypotenuse which determine the right angle are also referred to as “legs.” The side that makes a right angle with the base is called the perpendicular.
Thus, the definition of the hypotenuse in geometry can be given as the longest side in a right triangle that lies opposite to the right angle.
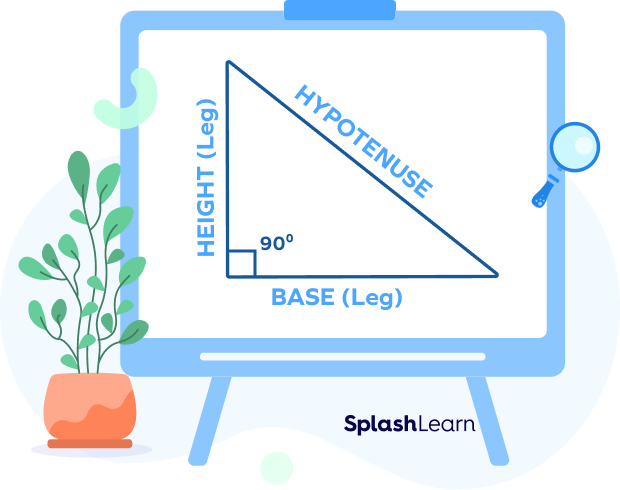
Theorem for the Hypotenuse
The famous Pythagoras’ theorem defines the hypotenuse theorem. As per this theorem, in a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides of the triangle, i.e., the base and perpendicular side.
Base² $+$ Perpendicular² $=$ Hypotenuse2
Proof of the Hypotenuse Theorem
Do you wonder how the hypotenuse theorem was derived? Let’s understand its proof.

The triangle ABC is a right-angled triangle such that m$\angle$B $= 90^{\circ}$.
AB is the base side, BC is the perpendicular side, and AC is the hypotenuse side.
We need to prove that AB² $+$ BC² $=$ AC²
For this, we draw a line from B to meet the side AC at point D.
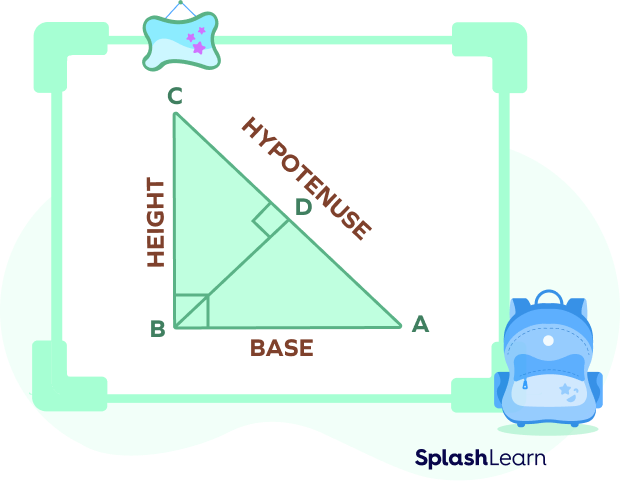
Using the similar triangle theorem, we get,
$\Delta$ADB ~ $\Delta$ABC by AAA similarity
Thus, its corresponding sides are proportional.
$\frac{AD}{AB} = \frac{AB}{AC}$
AB² $=$ AD $\times$ AC – (i)
Now, using the similar triangle theorem again, we get,
$\Delta$BDC ~ $\Delta$ABC
So, $\frac{AD}{AB} = \frac{AB}{AC}$
That is BC² $=$ CD $\times$AC – (ii)
Now, by adding (i) and (ii), we will get,
AB² $+$ BC² $=$ (AD $\times$ AC) + (CD $\times$ AC)
AB² $+$ BC² $=$ AC (AD $+$ CD)
AB² $+$ BC² $=$ AC (AC)
AB² $+$ BC² $=$ AC²
Or
AC² $=$ AB² $+$ BC²
We can also write this as
Hypotenuse² $=$ Base² $+$ Perpendicular²
Formula of the Hypotenuse
How to find the hypotenuse of a right triangle? We can use the formula that includes the length of the base and the perpendicular.
The formula for a hypotenuse is
Hypotenuse $= \sqrt{Base² + Perpendicular²}$
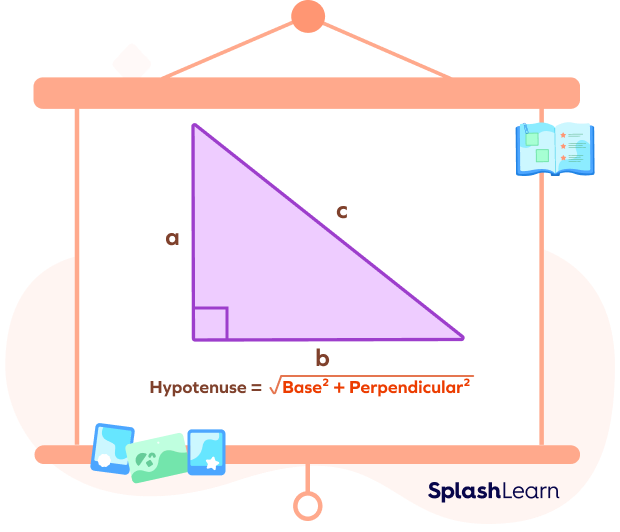
In a right-angled triangle ABC,
Hypotenuse $= c$
Base $= b$
Perpendicular or Altitude $= a$
$a^{2} + b^{2} = c^{2}$
How to Calculate the Length of the Hypotenuse of a Right Triangle?
Let’s understand the steps for the calculation of the length of the hypotenuse of a right triangle when base and height are given.
Example:
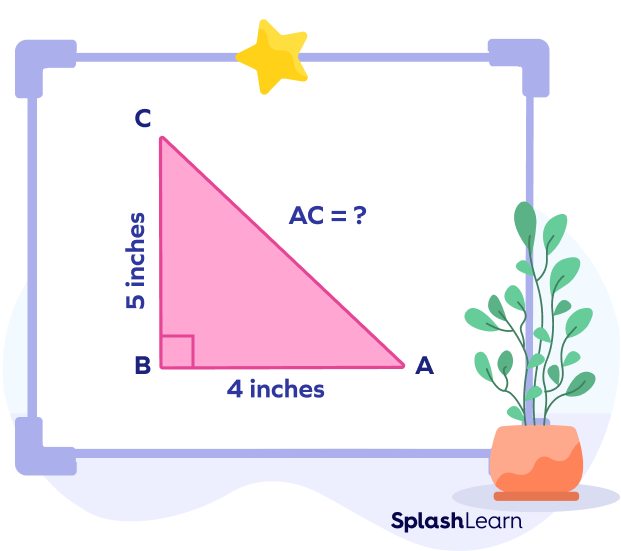
We know that the base side, i.e., AB $= 4$ inches, and the perpendicular side, i.e., BC $= 3$ inches.
To find the length of the hypotenuse, we need to use the above formula.
Hypotenuse $=$ Base² $+$ Perpendicular²
AC $= \sqrt{(AB)² + (BC)²}$
AC $= \sqrt{(4)² + (3)²}$
AC $= \sqrt{16 + 9}$
AC $= \sqrt{25}$
AC $= 5$ inches.
Thus, the hypotenuse of the right triangle ABC is 5 inches.
How To Find the Altitude Drawn on a Hypotenuse?
The altitude on a hypotenuse is the perpendicular drawn on the hypotenuse that connects a right triangle’s hypotenuse to its opposite vertex.
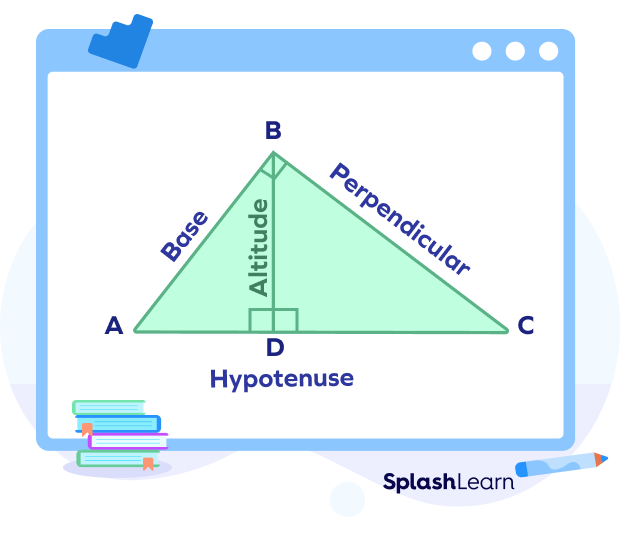
To find the altitude on a hypotenuse, let’s take an example.
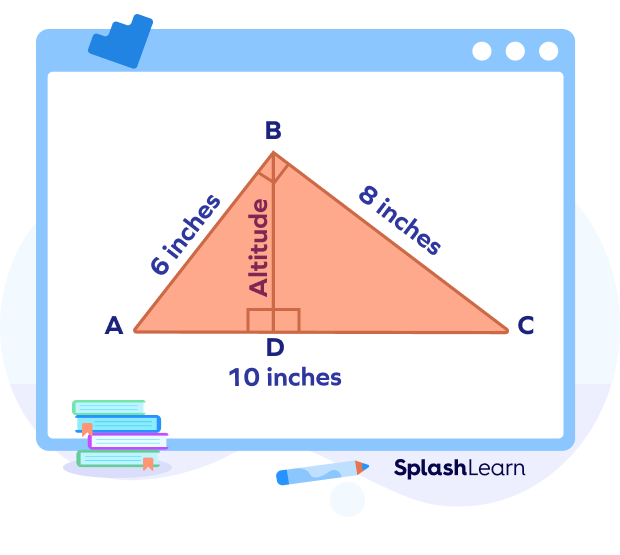
From the right-angled triangle ABC, we know that,
Base $= 6$ inches.
Perpendicular $= 8$ inches.
Hypotenuse $= 10$ inches.
To find the altitude, we divide the shortest side by the hypotenuse of $\Delta$ABC, i.e., Base/Hypotenuse $= \frac{6}{10} = \frac{3}{5}$.
Finally, we multiply this value by the value of the remaining side of the $\Delta$ABC, i.e.,
$\frac{3}{5} \times $ perpendicular $= \frac{3}{5} \times 8 = \frac{24}{5} = 4.8$.
Thus, the value of the altitude in $\Delta$ABC is 4.8 inches.
Area of an Isosceles Right Triangle
Generally, the area of an isosceles right triangle is calculated with the help of this simple formula:
Area $= \frac{1}{2}$ Base $\times$ Perpendicular (or altitude)
Since an isosceles right triangle has two equal sides, we can also write the formula as:
Area $= \frac{1}{2}\times$ (Base)²
Or
Area $= \frac{1}{2}\times$ (Perpendicular)².
For example: Calculate the area of the isosceles right triangle given below.
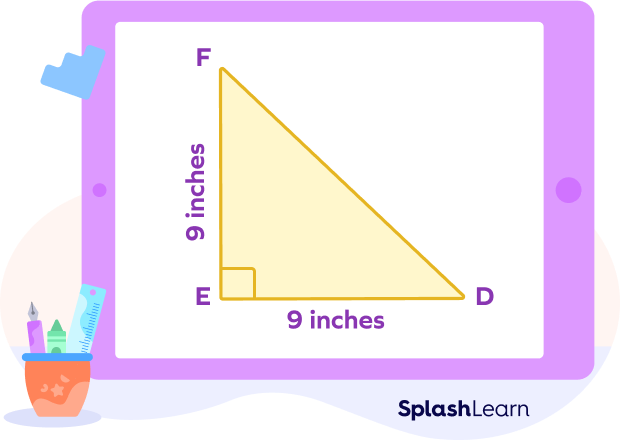
We know that the base side, i.e., DE $= 9$ inches.
So, the area of the isosceles right triangle $= \frac{1}{2}\times$ (Base)²
$=\frac{1}{2}\times$ (DE)²
$= \frac{1}{2}\times (9)²$
$= \frac{1}{2}\times 81$
$= 40.5$ inches².
In scenarios where only the hypotenuse of an isosceles right triangle is given, we can still find its area. Let’s understand this better with an example.
Example: Find the area of the isosceles right triangle whose hypotenuse is 12 feet.
We know that hypotenuse $= \sqrt{(base² + perpendicular²)}$
Since the triangle is isosceles, hypotenuse $= \sqrt{(base² + base²)}$
$12 = \sqrt{2(base)^{2}}$
$(12)² = 2(base²)$
Here, the squares on either side will cancel each other out, and we will get:
$12 = 2(base)$
$\frac{12}{2} \times = base$
$6 = base$.
Thus, the base $= 6$ feet $=$ perpendicular.
Now, since we know the sides of an isosceles triangle other than its hypotenuse, we can find its area by using the formula:
$\frac{1}{2} \times (Base)² = \frac{1}{2} \times (6)² = \frac{1}{2} \times 36 = 18$ inches².
Fun Facts
- Did you know that the word hypotenuse is derived from the Greek word hypoteinousa? “Hypoteinousa” means “stretching under (a right angle).”
- The relationship between altitude on a hypotenuse and a right-angled triangle is explained by the Right Triangle Altitude Theorem. As per this theorem, altitude on the hypotenuse of a right-angled triangle divides it into two congruent right-angled triangles. The two triangles are similar to the main right-angled triangle.
- In a right-angled triangle, the altitude on the hypotenuse can also be calculated with the help of basic trigonometric ratios.
Conclusion
In geometry, the hypotenuse is defined as the side opposite the right angle in a right-angled triangle. Its theorem is defined by Pythagoras’ theorem (Hypotenuse² $=$ Base² $+$ Perpendicular²). This formula helps us find the hypotenuse and area of a right triangle or an isosceles right triangle in math and for real-life objects as well.
Solved Examples on Hypotenuse
- Find the length of the hypotenuse DF.
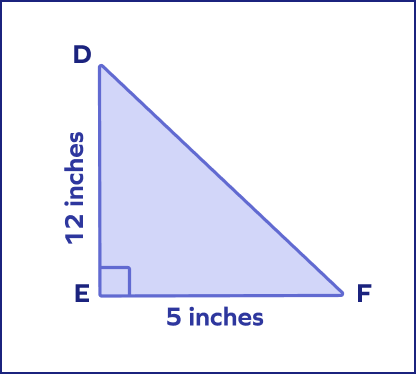
Solution:
Here, the base side (EF) $= 5$ inches and the perpendicular (DE) $= 12$ inches.
Hypotenuse $= \sqrt{(base² + perpendicular²)}$
$= \sqrt{\left\{(5)² + (12)²\right\}}$
$= \sqrt{25+144}$
$= \sqrt{169}$
$= 13$ inches.
Thus, the length of the hypotenuse (DF) is 13 inches.
2. Hypotenuse $= 100$ feet, Base $= 8$ feet. Find the height of the right triangle.
Solution:
We know that
Hypotenuse² $=$ Base² $+ $Perpendicular².
$100 = 8^{2} +$ Perpendicular²
Perpendicular² $= 100 \;-\;64$
Perpendicular² $= 36$
Perpendicular $= 6$ feet
3. Find the area of a right triangle whose base and perpendicular are 10 feet each.
Solution:
When the triangle is isosceles (base side = perpendicular side), the formula finding the area
$= \frac{1}{2} \times$(perpendicular)²
$= \frac{1}{2} \times (10)² $
$= \frac{1}{2} \times 100$
$= 50$ feet².
4. Find the base of the right-angled sandwich.
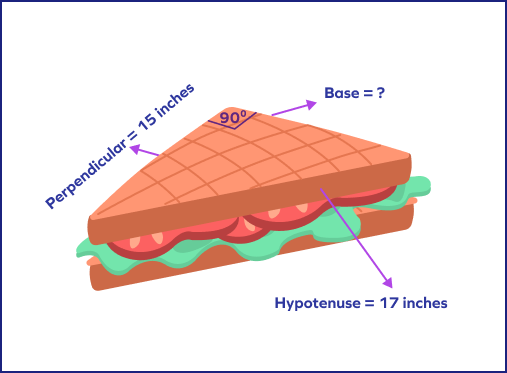
Solution: We know that hypotenuse $= 17$ inches and perpendicular $= 15$ inches.
Since hypotenuse² $=$ (base² $+$ perpendicular²).
So, base² $=$ (hypotenuse² $-$ perpendicular²)
base² $= (17)² \;-\; (15)²$
base² $= 289 \;-\; 225$
base² $= 64$
base² $= (8)²$
Squares on each side will cancel each other, and we will get,
Base $= 8$ inches.
5. Determine the altitude of a right triangle whose hypotenuse, base, and perpendicular are 15, 9, and 12 inches.
Solution: To find the altitude, we need to divide the shortest side (here, base) by the hypotenuse.
Base/Hypotenuse $= \frac{9}{15} = \frac{3}{5}$.
Now, we need to multiply the above value by the remaining side, i.e., the perpendicular side.
$\frac{3}{5} \times$ perpendicular $= \frac{3}{5} \times 12 = \frac{36}{5} = 7.2$
Thus, the altitude of the right triangle is 7.2 inches.
Practice Problems on Hypotenuse
Hypotenuse in Right Triangle
Hypotenuse is ______________.
The hypotenuse is the side that lies opposite to the right angle.
Find the length of the perpendicular of a right triangle whose base is 7 inches and whose hypotenuse is 25 inches.
Hypotenuse² $=$ Base² $+$ Perpendicular²
So, Perpendicular² $=$ Hypotenuse² $-$ Base²
Perpendicular² $= (25)² \;-\; (7)² = 625 \;-\; 49 = 576$
Perpendicular² $= (24)²$
Perpendicular $= 24$ inches.
The longest side of the right-angled triangle is called ____________.
Hypotenuse is the longest side of the right-angled triangle.
In the following image, a and b are ____.
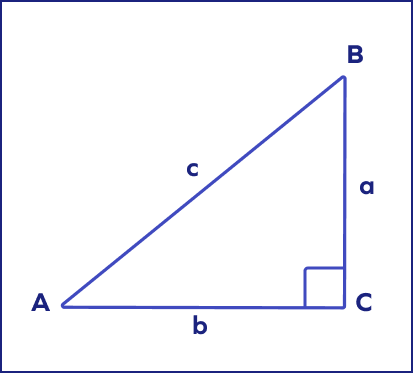
In right triangles, the base and the perpendicular are also called legs.
Find AC.
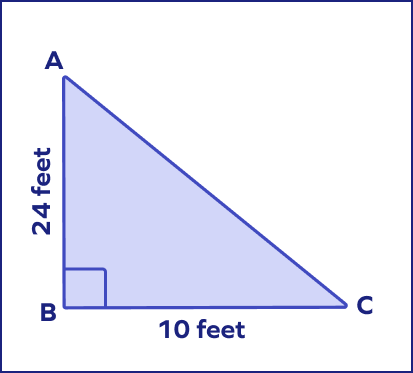
AC $= \sqrt{(AB)² + (BC)²}$
AC $= \sqrt{(24)² + (10)²}$
AC $= \sqrt{(576 + 100)} = \sqrt{676} = 26$ feet.
Frequently Asked Questions on Hypotenuse
What is the similar triangle theorem?
The similar triangle theorem states that two triangles are similar when their corresponding angles are congruent, and their sides are proportionately equal.
Can you find the hypotenuse of other triangles other than the right triangle?
No. In geometry, the hypotenuse is only defined for right-angled triangles and not for any other type of triangle.
What are the sides of a right triangle collectively called?
The sides of a right triangle are collectively known as Pythagorean triplets.
















