What is The Area of a Square?
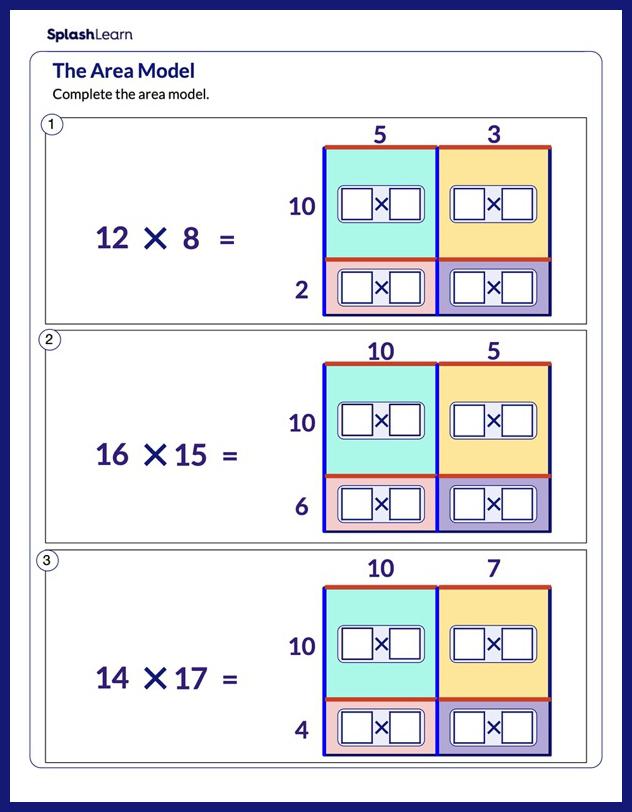
The number of square units needed to fill a square is its area. In common terms, the area is the inner region of a flat surface (2-D figure).
In the given square, the space shaded in violet is the area of the square.

For example, The space occupied by the swimming pool below can be found by finding the area of the pool.

Recommended Games
The Formula for the Area of A Square
The area of a square is equal to (side) × (side) square units.
The area of a square when the diagonal, d, is given is d2÷2 square units.
For example,
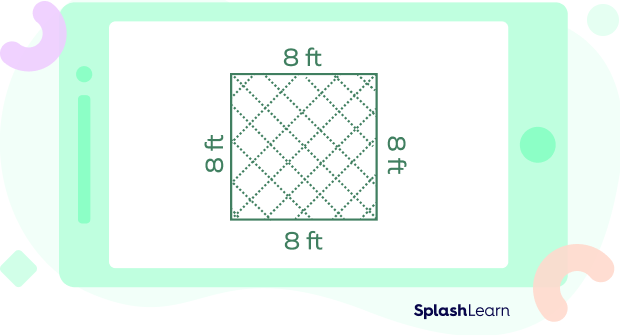
The area of a square with each side 8 feet long is 8 × 8 or 64 square feet (ft2).
Recommended Worksheets
Solved Examples On Area of a Square
Example 1: Given that each side is 5 cm, find the area of a square.
Solution:
Area of a square = side × side
Area = 5 × 5
Area = 25 cm2
Example 2: The side of a square wall is 50 m. What is the cost of painting it at the rate of Rs. 2 per sq. m?
Solution:
Side of the wall = 50 m
Area of the wall = side × side = 50 m × 50 m = 2500 sq. m
The cost of painting 1 sq. m = Rs. 2
Thus the cost of painting a 2500 sq. m wall = Rs. 2 × 2,500 = Rs 5,000
Example 3: Find the area of a square whose diagonal is measured is 4 cm.
Solution:
Given:
Side, d = 4 cm
We know that the formula to find the area of a square when the diagonal, d, is given is d2÷2 square units.
Substituting the diagonal value, we get:
= 42÷2 = 16 ÷ 2 = 8
Thus, the area of the square is 8 cm2.
Practice Problems On Area of a Square
Area Of A Square
What is the area of a square table whose diagonal is 6 feet?
The formula to calculate the area of the square when the diagonal is given is d2/2. Here, the length of the diagonal = 6 ft As per the formula, it can be written as:
Area of Square= 6$^{2}$/2
= 36/2
= 18
Thus, the area of the square table is 18 sq feet.
Calculate the floor area of the square room, furnished by 250 square tiles of sides 30 inches.
Total number of tiles = 250 Side of one tile = 30 inches Area of 1 tile = 30 x 30 inches
= 900 square inches
So, the area occupied by 200 tiles of sides 30 inches = Area of one tile x Total number of tiles
Total Floor Area = 900 x 200 square inches
= 180000 sq inches
The area of the square garden is 784 m2. Find out the length of the garden?
Answer: Area of garden = 784 m$^{2}$
Side of the garden = ?
We know the formula to calculate the side of the square or garden, A = Side$^{2}$
It can be written as,
784 m$^{2}$ = Side$^{2}$
Therefore, side of the garden = $\sqrt{784}$
= 28 meters
Find the area of the square swimming pool whose side is 18 m.
324 m$^{2}$
Side of the swimming pool, or a = 18m
Area of swimming pool = a$^{2}$
= 18 x 18
= 324 m$^{2}$
Frequently Asked Questions On Area of a Square
What is the difference between the perimeter and area of a square?
The perimeter of a square is the sum of its four sides or the length of its boundary. It is a one-dimensional measurement and expressed in linear units. Area of a square is the space filled by the square in two-dimensional space. It is expressed in square units.
How do you calculate the area of a square if the perimeter is given?
The perimeter of the square is the sum of all four sides of the square. If the perimeter is given, then the formula to calculate the area of the square, A = Perimeter2/16
What are the units of the area of the square?
The area of the square is 2-dimensional. Thus, the area of the square is always represented by square units, for which the common units are cm2, m2, in2, or ft2.
Do two squares of equal areas have equal perimeters?
Yes. Two squares of equal areas, given by side x side, will have the same side lengths. They are congruent. Consequently, the perimeters of the two squares, given by 4 x side length, will be equal as well.
Conclusion
To learn similar concepts, head over to SplashLearn. The game-based learning platform has interactive games, worksheets, and courses that make learning fun and intriguing. Enjoy the flexible time schedule, and get the best-curated knowledge from highly qualified professional teachers.