What is a “Millimeter”?
“Millimeter” is a unit of length that equals one-thousandth of a meter. It is a small unit of measurement compared to the centimeter, meter, inches, and feet we are familiar with.
Here’s a fun example to understand why small units are important. Do you know the story of Gulliver? Gulliver, a sea captain and a surgeon, ends up on the island of Lilliput, where people are only about 6 inches in height. Everything in the town is so small, he has to document everything in smaller units like inches and millimeters (mm). Can you imagine measuring tiny things using units like yards or miles? So, small units of measurement are important! So, what is mm in measurements? Let’s learn more about the unit ‘millimeter’.

Recommended Games
Millimeter Definition
A millimeter is a unit measuring length in the metric system. “Milli” comes from the Latin word “mille,” meaning one-thousandth. Therefore, a millimeter is one-thousandth of a meter. The symbol of a millimeter is “mm.”
In case you are wondering how to measure length in millimeters or how a length of a millimeter or 1 mm looks like, let’s check it out on a ruler.
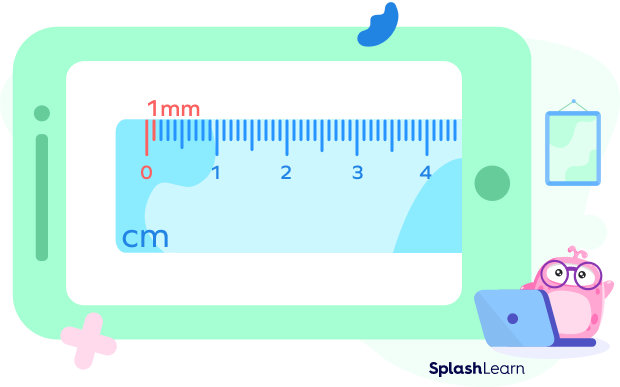
Understand that 1 meter $= 100$ cm and 1 cm $= 10$ mm. On the metric ruler (mm ruler), the distance between two big lines is 1 cm. However, between them, you will find 10 equal smaller lines of length 1 mm each.
Recommended Worksheets
Millimeter and Other Units of Length
We can use the following conversion chart to convert millimeters into different metric units of length.
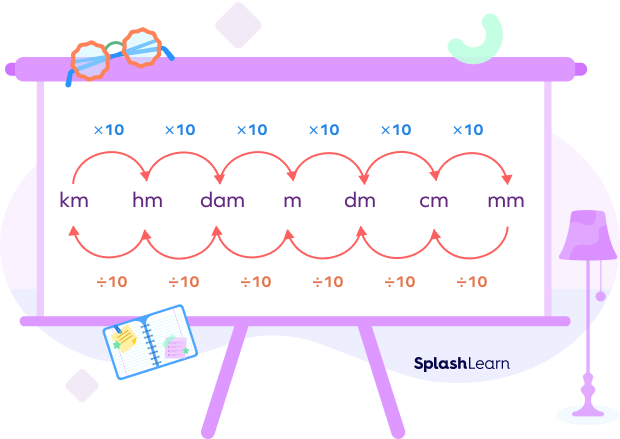
We have to multiply the length by 10 every time we move from left to right. Also, for each time we move from left to right, we must divide the length by 10.
Millimeter and Metric Units
Hence, from the above chart, we can conclude:
- 1 mm (1 millimeter) $= 1$ mm
- 1 cm (1 centimeter) $= 1 \times 10$ mm $= 10$ mm
- 1 dm (1 decimeter) $= 1 \times 10 \times 10$ mm $= 100$ mm
- 1 m (1 meter) $= 1 \times 10 \times 10 \times 10$ mm $= 1000$ mm
- 1 dam (1 decameter) $= 1 \times 10 \times 10 \times 10 \times 10$ mm $= 10,000$ mm
- 1 hm (1 hectometer) $= 1 \times 10 \times 10 \times 10 \times 10 \times 10$ mm $= 100,000$ mm
- 1 km (1 kilometer) $= 1 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10$ mm $= 1,000,000$ mm
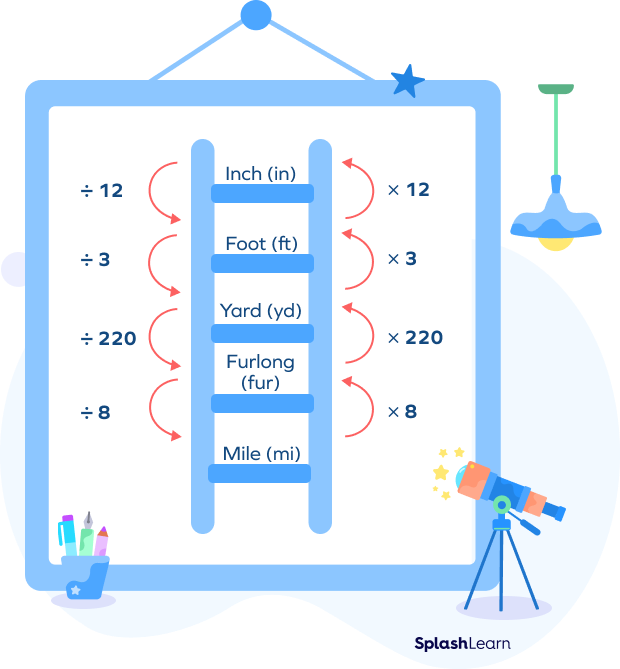
Millimeter and Other Customary Units
1 yard $= 0.9144$ meters
We can use the following chart to find the approximate results for the conversion of customary units.
Example 1: Convert 147.5 mm into cm.
We can use the conversion chart to convert 147.5 mm into cm.
As we can see in the chart, from mm to cm, only one jump to the left is required. So, we have to divide the length by 10.
So, 147.5 mm $= 147.5 \div 10$ cm $= 14.75$ cm
Example 2: Convert 3 ft into mm.
From the conversion chart, we have to climb one step down from ft to yd. So, 3 ft $= 3 \div 3 = 1$ yd
Now, we know that one yd $= 0.9144$ m.
From the conversion chart, from m, we have to jump three points to the right to reach mm. So, we have to multiply 0.9144 by 10 x 10 x 10.
Therefore, 1 yd $=$ 0.9144 m $= 914$.4 mm
Solved Examples
1. Convert 1 mm into a decimeter.
Solution: From the above conversion chart, we have to jump two sides to the left to reach dm from mm. So, we have to divide 1 mm by $10 \times 10$ or 100.
So, 1 mm $= \frac{1}{100} =$ 0.01 dm.
2. The length of a football pitch is 105 m. Express it in mm.
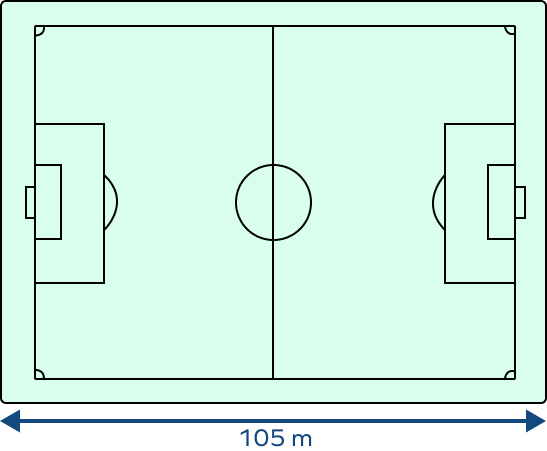
Solution: From the above chart, from m, we have to jump three times to the right to reach mm. So, we have to multiply 105 m with $10 \times 10 \times 10 = 100$.
So, 105 m $= 105 \times 100$ mm $= 105$,000 mm.
Therefore, the length of a football pitch is 105,000 mm.
3. What is the height of the small replica of a palace shown below in meters?

Solution: First, let us convert 750 mm into m.
To reach m from mm, we must jump three places to the left. So, we have to divide 750 by $(10 \times 10 10)$ or 1000.
So, 750 mm $= 750 \div 1$,000 m $=$ 0.75 m.
Therefore, the length of the palace is 0.75 m.
Practice Problems
Millimeter
The average length of a red ant is 5 mm. Express it in meters.
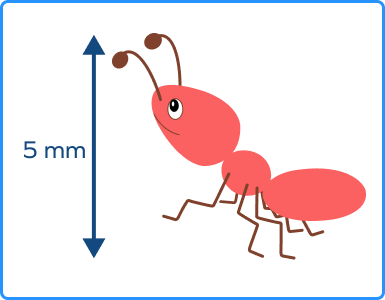
From the chart, mm is three positions left to m. So, we divide by 1000.
1 mm $= 1 \div (10 \times 10 \times 10)$ m.
$= 1 \div 1000$ m
$= 0.001$ m.
So, 5 mm $= 0.001 \times 5 = 0.005$ m.
Express 3 km in mm.
From the conversion chart, 3 km $= (3 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10)$ mm $= 3,000,000$ mm.
Convert 8,540,000 mm into hectometers.
From the chart, 8,540,000 mm $= \frac{8,540,000}{10 \times 10 \times 10 \times 10 \times 10}$ hm
$= \frac{8,540,000}{100,000}$
$= \frac{8,54}{10}$
= 85.4 hm
Convert 2 furlongs into mm.
From the conversion chart, we must climb one step up to reach the yard from the furlong.
So, 2 fur $= 2 \times 220$ yd $= 440$ yd.
We know that 1 yard $= 0.9144$ m.
So, 440 yd $= 440 \times 0.9144$ m $= 402.336$ m.
Now, from the conversion chart,
402.336 m $= 402.336 \times 10 \times 10 \times 10$ mm
$= 402.336 \times 1000$
$= 402,336$ mm
1 mile $= \underline{}$ mm
We know that 1 mi $= 1,760$ yards.
But 1 yd $= 914.4$ mm.
So, 1 mi $= 1760 \times 914.4$ mm $= 1,609,344$ mm.
Frequently Asked Questions
We have measures like meters and kilometers to express bigger distances, like the distance between two cities, the height of mountains, lengths of rivers, etc. However, the length of the wheat grain, the size of an ant, the thickness of a paper, etc., are some measures we find difficult to express in bigger units of measurement like meters. Here, millimeters help us accurately express their length.
Is a millimeter the smallest unit of measurement?
A millimeter is usually the smallest unit you can measure using a regular ruler. However, there are many units smaller than a millimeter. The smallest unit of measuring length is Planck Length.
How many inches are in one millimeter?
One millimeter equals approximately 0.039 inches.
What are some real-life objects having a 1 mm dimension?
Some examples of objects having about 1 millimeter length areA sharp pencil point and the tip of a sewing needle are approximately 1 mm in length.































