What Is a Factor in Math?
A factor of a number is a number that divides the given number evenly or exactly, leaving no remainder.
Note that when studying factors of a number, we only consider positive integers. A factor cannot be a fraction or a decimal. Also, since division by 0 is undefined, 0 cannot be a factor of any number.
To check if x is a factor of a certain number n, simply divide n by x. If the remainder is 0, then x is a factor of n. Otherwise, x is not a factor of n.
Examples:
| Division | Remainder | Is the number a factor? |
|---|---|---|
| $21 \div 7 = 3$ | Remainder $= 0$ | Yes, 7 is a factor of 21. |
| $6 \div 3 = 2$ | Remainder $= 0$ | Yes, 3 is a factor of 6. |
| $8 \div 2 = 4$ | Remainder $= 0$ | Yes, 2 is a factor of 8. |
| $5 \div 1 = 5$ | Remainder $= 0$ | Yes, 1 is a factor of 5. |
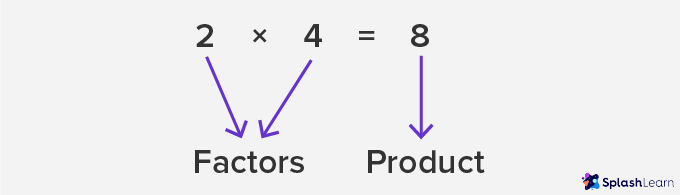
We know that division and multiplication are inverse operations (opposite operations). Thus, we can also define factors in math in terms of multiplication.
If we can express the given number as the product of two positive integers, then both the integers are factors of the given number. A general formula to remember is that a and b are factors of the product ab.
Examples:
| Product | Factors |
|---|---|
| $7 \times 3 = 21$ | Both 7 and 3 are factors of 21. |
| $2 \times 4 = 8$ | Both 2 and 4 are factors of 8. |
| $2 \times 3 = 6$ | Both 2 and 3 are factors of 6. |
| $9 \times 3 = 27$ | Both 3 and 9 are factors of 27. |
| $7 \times 5 = 35$ | Both 5 and 7 are factors of 35. |
Recommended Games
Factor of a Number: Definition
A factor of a number can be defined as a number that divides the given number without leaving any remainder.
Recommended Worksheets
How to Find Factors of a Number
There are different methods of finding factors, such as multiplication and division. We can also use the rules of divisibility to find factors of a number by checking if the given number is divisible by a certain set of numbers or not.
Finding Factors of a Number by Multiplication Method (Bold)
If we can express the given number as the product of two whole numbers, then the numbers being multiplied are factors of the product.
Thus, to find all the factors of a number, find all the pairs of numbers that, when multiplied, give the given number as a product.
Example 1: Let us consider the number 8. 8 can be written as
$8 = 1 \times 8$
$8 = 2 \times 4$
As a result, the factors of 8 are 1, 2, 4, 8.
Example 2:
| Product | Factors of 18 |
|---|---|
| $1 \times 18 = 18$ | The factors of 18 are 1, 2, 3, 6, 9, and 18. |
| $2 \times 9 = 18$ | |
| $3 \times 6 = 18$ |
Finding Factors of a Number by Division Method (Bold)
We can find the factors of a number by dividing the number by all possible divisors.
To find all the factors of a number n using the division method, divide the number by all the natural numbers less than n. Identify the numbers that completely divide the given number.
Note that when you identify one such factor by division method, the quotient obtained in that division is also a factor.
Example: Find all the factors of the number 10.
| Division | Is the number a factor of 10? |
| $10 \div 1 = 10$ and remainder $= 0$ | Yes, 1 is a factor of 10.(Also, the quotient 10 is also a factor of 10.) |
| $10 \div 2 = 5$ and remainder $= 0$ | Yes, 2 is a factor of 10.(Also, 5 is also a factor of 10.) |
| $10 \div 3 = 3$ and remainder $= 1$ | No, 3 is not a factor of 10. |
| $10 \div 4 = 2$ and remainder $= 2$ | No, 4 is not a factor of 10. |
| $10 \div 5 = 2$ and remainder $= 0$ | Yes, 5 is a factor of 10. |
| $10 \div 6 = 1$ and remainder $= 4$ | No, 6 is not a factor of 10. |
| $10 \div 7 = 1$ and remainder $= 3$ | No, 7 is not a factor of 10. |
| $10 \div 8 = 1$ and remainder $= 2$ | No, 8 is not a factor of 10. |
| $10 \div 9 = 1$ and remainder $= 1$ | No, 9 is not a factor of 10. |
| $10 \div 10 = 1$ and remainder $= 0$ | Yes, 10 is a factor of 10. |
Thus, the factors of 10 are 1, 2, 5, and 10.
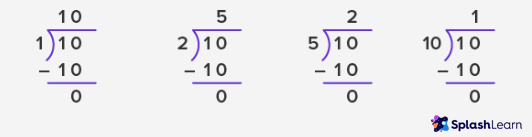
Properties of Factors
- The smallest factor of any number is 1.
- The largest factor of any number is the number itself.
- All integers have a finite number of factors.
- A factor is always less than or equal to the number; it can never be bigger than the number.
- Except for 0 and 1, every integer has a minimum of two factors: 1 and the number itself.
Factor Pairs
A factor pair refers to the pair of integers that, when multiplied together, give us the required number. Factor pairs of a number do not include fractions.
As mentioned earlier, we only consider positive factors when we study or list the factors of a number. However, the concept of factor pairs includes both positive and negative integers.
For every positive factor pair, we have a corresponding negative factor pair, since the product of two negative integers is always positive.
| Positive Factor Pairs of 14 | Negative Factor Pairs of 14 |
|---|---|
| $1 \times 14 = 14 \Rightarrow (1, 14)$ | $(\;-\;1) \times (\;-\;14) \Rightarrow = 14 (\;-\;1,\; \;-\;14)$ |
| $2 \times 7 = 14 \Rightarrow (2, 7)$ | $(\;-\;2)\times (\;-\;7) = 14 \Rightarrow (\;-\;2,\; \;-\;7)$ |
Different Types of Factors
- Prime Factors: The factors of a number which are also prime numbers are called Prime factors. Prime numbers are numbers that have only two factors, 1 and the number itself.
For example, the factors of 6 are 1, 2, 3, and 6. Out of these, the prime factors of 6 are 2 and 3.
- Common Factors: Common factors of two numbers are the factors common to (or shared by) both the numbers.
Factors of 4: 1, 2, 4
Factors of 6: 1, 2, 3, 6
Common factors of 4 and 6: 1, 2
- Greatest Common Factor: The greatest number among the common factors identified between the two numbers is called the Greatest Common Factor (GCF). In the previous example, the common factors of 4 and 6 are 1 and 2. The GCF is 2.
Prime Factorization
When we write a number as a product of all its prime factors, it is called prime factorization. Every number in prime factorization is a prime number. To write the number as a product of prime factors, sometimes we might have to repeat the factors too.
Example 1: To write the prime factorization of 8, we can write
$8 = 2 \times 2 \times 2$
The prime factor 2 is repeated three times.
Example 2: Prime factorization of 30
$30 = 2 \times 3 \times 5$
Real-life Applications of Factorization
Equal division: If six people come together to eat a whole pizza that has been cut into 24 slices, it would only be fair that everyone receives an equal number of slices. Therefore, this pizza can be divided into equal shares because 6 (the number of people) is a factor of 24 (the number of pizza slices). When you divide 24 by 6, you get 4, and each individual receives four slices!
Factoring and money: The exchange of money and its divisions into smaller units rely heavily on factoring. For example, four quarters equal one dollar in America.
Facts about Factors
- If a number has more than two factors (but a finite number of factors), it is called a composite number.
- Factors are never decimals or fractions; they are only integers.
- All even numbers have 2 as a common factor.
- 5 is a factor of all numbers that end in 0 and 5.
- All numbers ending in a 0 have 2, 5, and 10 as factors.
- If the prime factorization of a number is of the form $p^{a}\;q^{b}$, where p and q are its
prime factors, then the total number of factors of a given number are given by
$(a + 1)(b + 1)$, where a and b are the exponents in the prime factorization.
Example: $18 = 2^{1} \times 3^{2}$
Total number of factors of $18 = (1 + 1)(2 + 1) = 6$
Factors of 18 are 1, 2, 3, 6, 9, 18.
Solved Examples on Factor in Math
Example 1: Find all the factors of 20.
Solution:
Step 1: Write all the numbers from 1 to 20.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Step 2: Now check which of these numbers are divisible by 20 and leave no remainders.
$20 \div 1 = 20$ and remainder $= 0$
$20 \div 2 = 10$ and remainder $= 0$
$20 \div 3 = 6$ and remainder $= 2$ (not divisible)
Continue dividing 20 by each of these numbers.
Step 3: The factors of 20 are 1, 2, 4, 5, 10, and 20.
Example 2: Find all the factors of 31.
Solution:
31 is a prime number. The only two numbers that divide 31 completely are 1 and 31.
Therefore, factors of 31 are 1 and 31.
Example 3: Find the prime factors of 144.
Solution:
Prime factorization is the method of expressing a given number as the product of its prime factors. Prime factors are factors that are also prime numbers. The factors of any prime number are 1 and the number itself. For example, 13 is a prime number because the factors of this number are 1 and 13.
Consider the number 144. Start by dividing 144 by the smallest possible prime factor, which is 2.
$144 = 2 \times 72$
$144 = 2 \times 2 \times 36$
$144 = 2 \times 2 \times 2 \times 18$
$144 = 2 \times 2 \times 2 \times 2 \times 9$
$144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3$
Thus, the prime factors of 144 are 2 and 3.
Practice Problems on Factor in Math
Factor in Math – Definition, Types, Properties, Examples, Facts
Which of the following options represents all the factors of the number 10.
Factors of 10 are 1, 2, 5, and 10.
We can easily eliminate all other options in which factor 3 is present since the number 3 does not divide number 10 completely.
Which of the following options represents all factors of the number 27.
Factors of 27 are 1, 3, 9, and 27.
Note that we can easily eliminate other options since the numbers 4 and 5 are not factors of 27.
Which of the following options represents all the factors of 12?
Factors of 12 are 1, 2, 3, 4, 6, and 12.
These numbers divide 12 evenly.
Select the option with all the factors of the number 15?
There is no remainder left when 15 is divided by 1, 3, 5, and 15.
Frequently Asked Questions of Factorization
What are the factors in math?
A factor is a number that can be multiplied to create a specific number in math (for example, 5 and 8 are factors of 40).
How is factoring used in real life?
In real life, factoring is a valuable skill. Typical applications include dividing something into equal portions, exchanging money, comparing prices, understanding time, and making computations while traveling.
What is the importance of learning about prime factors?
Prime numbers are used in prime factorization to break down composite numbers into their prime factors, which is important in various mathematical computations and problem-solving. We can easily find LCM and GCD of two numbers using prime factorization. Prime numbers also have important applications in number theory, cryptography and the field of computer security.
How do you find the factor in math?
Here is a step-by-step guide to finding the factor of any number in math.
- Start by considering the smallest natural numbers like 2, 3, etc.
- Divide the number by the smallest natural number that it could be divided by.
- Continue dividing the number by the smallest possible natural number, which gives 0 as the remainder.
- Stop when the number is wholly divided to give 1 as the quotient.
- The numbers that you used for dividing the original number are the factors of the number.
What does factor mean in math?
The meaning of the term ‘factor’ in math can be explained as a number that divides the given number exactly with 0 remainder.
What is a factor in multiplication?
If we multiply two numbers to get a product, then each of the numbers being multiplied is considered as a factor of the product.
What are the factors of 24?
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.




































