What is Multiplicative Comparison?
A multiplicative comparison involves comparing two quantities such that when one is multiplied by a specified number, the other is produced.
For example, Sam has twice as many balloons as Sid.
 Sid has 3 balloons. |  Sam has twice as many balloons as Sid.So, the number of balloons with Sam = 2 × 3 = 6 |
Problems involving multiplicative comparison are generally word problems that can be solved by creating a multiplication equation.
A problem based on multiplicative comparison can have:
- A statement that compares two sets of items.
- It leads to a multiplication equation.
- The equation could have a symbol or a letter standing for the unknown quantity.
Example:
A building is 18 feet tall. The building is 3 times Jerry’s height. How tall is Jerry?
Let Jerry’s height be h feet.
The height of the building is 18 feet, which is 3 times Jerry’s height.
Therefore, 18 = 3 × h
(Think: What multiplied by 3 is 18?)
We know: 18 = 3 × 6
Therefore, the h, standing for Jerry’s height in the equation 18 = 3 × h, must be 6.
So, Jerry is 6 feet tall.
Problems involving multiplicative comparison usually have phrases like:
- Times as many (Jake has 5 times as many stamps as Ben.)
- Times as much (My sister earns 3 times as much as I do.)
- Times as long (A yard is 3 times as long as a foot.)
- Times the height (The building is 4 times the height of the tree.)
Here is an example of how to solve a multiplicative comparison word problem using comparison bar models.
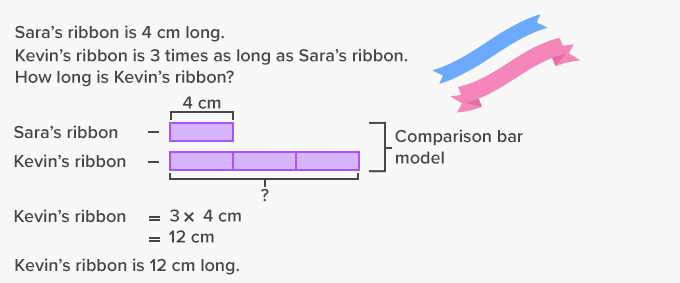
| Fun Facts 1. Bar models help us understand what operation (addition, subtraction, multiplication, division) should be used to solve the given problem. 2. Any two factors and their product can be read as a comparison statement (5 × 6 = 30: 30 is 5 times as much as 6).In a multiplicative comparison problem, one quantity is always smaller or larger than the other quantity. |
















