What Is a Thousand in Math?
In math, “thousand” refers to the four-digit natural number 1000, often written as “1,000” in numerical notation. The comma in “1,000” signifies the division between place values of digits.
The term “thousand” is used to represent a quantity or a value equivalent to 1,000, a number consisting of four digits.
- One thousand = 1,000
- Two thousand = 2,000
- Three thousand = 3,000
…and so on.
NOTE: Note that numbers with four or more digits, starting from 1,000, are written with a comma. This practice helps in understanding place values and periods, and thereby simplifying reading very large numbers. However, some American notations skip commas when writing four-digit numbers; they are typically used for numbers consisting of five digits or more. In some languages, the comma (,) is not used as a separator to prevent confusion with decimal placement.
Recommended Games
Thousand: Definition
A thousand (written as 1,000) is a natural number, which is a successor of the number 999 and the predecessor of the number 1,001.
In the decimal system, 1,000 holds a significant place, as it represents the power of 3, which can be expressed as 103. This means 1,000 is obtained by multiplying 10 by itself three times.
10 10 10 = 1,000
Recommended Worksheets
How to Write One Thousand in Different Ways
- Numerical notation: In numerical notation, the one thousand number is written as 1,000.
- Scientific notation: In scientific notation, a thousand is written as 1 × 103.
1,000 = 1 × 103
- Power of 10: 1,000 = 1 × 103
Why Is ‘1K’ Used to Represent One Thousand?
The letter “K” is frequently used to denote a thousand, especially in financial contexts or when writing large numbers. This convention comes from the Greek word “kilo,” which means a thousand.
So, what does K mean in math? In mathematics and numerical notations, the letter “K” represents a thousand. Thus, the “1K” is equivalent to 1,000. This simplifies reading and writing large numbers. For example, $10K stands for ten thousand dollars.
One Thousand vs. One Thousandths
Decimal fractions refer to the decimal form of fractions, whose denominator is 10 or higher powers of 10 such as 102 = 100, 103 = 1,000, 104 = 10,000, and so on. Decimal fractions with 1,000 as a denominator are also called thousandths.
- One thousandth = 0.001 $= \frac{1}{1000}$
- One thousand = 1,000
Thousands Period and Thousands Place in the International Place Value Chart
In the international place value system, there are three periods for the nine digits starting from the right: Ones, Thousands, and Millions
Three place values under the thousands period are thousands, ten thousands, and hundred thousands.
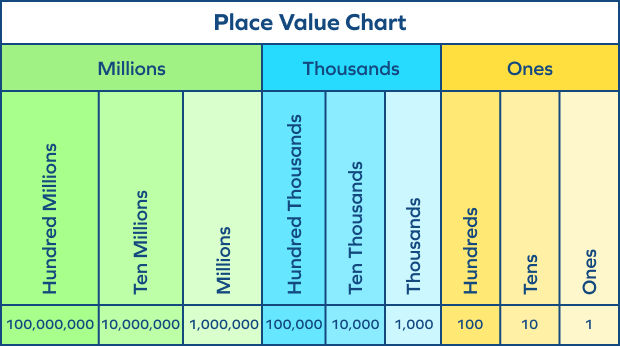
- Place Values of Digits in 1,000 (Bold)
In math, every digit in a number has a place value.
Place value can be defined as the value represented by a digit in a number on the basis of its position in the number. In the decimal system, place values of digits are represented by multiplying the digit by the corresponding powers of 10.
In the number 1,000, the three zeros belong to the ones period, each having the place value of 0. The digit 1 lies in the thousands period, at the thousands place. It has the place value of 1103= 1,000.
| Thousands | Hundreds | Tens | Ones |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 1 × 103 = 1,000 | 0 × 102 = 0 | 0 × 101 = 0 | 0 × 100 = 0 (100 = 1) |
- How to Represent Thousands Using Base Ten Blocks (Bold)
Base ten blocks are tools or manipulatives used to teach place values. For example, unit blocks (representing ones), rods (representing tens), flats (representing hundreds), and cubes (representing thousands).
A cube, also known as a thousand cube, is used to represent one thousand. It is constructed by assembling one thousand unit cubes together.

- Face Value of Digits in 1,000 (Bold)
Face value is the actual value of the digit in a number regardless of its position within the number.
Face value of 1 = 1
Face value of 0 = 0
Face value of 0 = 0
Face value of 0 = 0
Factors of 1,000
Factors of a thousand are the numbers that divide 1,000 exactly, without a remainder. The number 1,000 has 16 factors in total.
1,000 = 1 × 1,000
1,000 = 2 × 500
1,000 = 4 × 250
1,000 = 5 × 200
1,000 = 8 × 125
1,000 = 10 × 100
1,000 = 20 × 50
1,000 = 25 × 40
The factors of 1,000 are 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, and 1,000.
Facts about Thousand
- 1,000 millimeters = 1 meter
- 1,000 meters = 1 kilometer
- In finance and everyday language, the letter “K” is used as an abbreviation to represent a thousand. For example, $\$10K$ means ten thousand dollars.
- Thousand thousand (one followed by 6 zeros) equals one million.
- 1 million = 1000,000
Conclusion
In this article, we have learned about a thousand in math. The number 1,000 acts as a fundamental building block for comprehending our numerical system in the world of mathematics. Now, let’s solve some examples and practice problems to understand the concept better.
Solved Examples on Thousand
Example 1: Convert 3 km into meters.
Solution:
There are 1,000 meters in one kilometer.
To convert kilometers to meters, you can multiply the number of kilometers by 1,000.
3 kilometers = (3 × 1,000) meters = 3,000 meters
So, 3 kilometers is equivalent to 3,000 meters.
Example 2: Find the prime factorization of the number 1,000.
Solution:
To find the prime factorization of 1,000, we can start by dividing it by prime numbers.
1,000 = 2 × 500
1,000 = 2 × 2 × 250
1,000 = 2 × 2 × 2 × 125
1,000 = 2 × 2 × 2 × 5 × 25
1,000 = 2 × 2 × 2 × 5× 5 × 5
1,000 = 23 × 53
Example 3: Express the fraction $\frac{7}{1,000}$ as a decimal.
Solution:
To convert a fraction into a decimal, divide the numerator by the denominator.
7 ÷ 1,000 = 0.007
Thus, $\frac{7}{1,000} = 0.007$
Practice Problems on Thousand
Thousand (1,000) in Math - Definition, Facts, Examples, FAQs
How is 1,000 typically represented in scientific notation?
In scientific notation, 1,000 is expressed as $1 \times 10^{3}$.
Which metric prefix is used to represent 1,000 in the International System of Units (SI)?
In the SI system, kilo represents a factor of 1,000.
How many hundreds make one thousand?
There are 10 hundreds in one thousand.
$10 \times 100 = 1,000$.
What is the place value of digit 1 in 1,000?
In the number 1,000, the digit 1 is in the thousand's place, so its value is 1 multiplied by $10^{3}$(which is 1,000).
How many 0s are there in a thousand?
The word thousand denotes a quantity or value equal to 1,000. Thus, there are three 0 in a thousand
Frequently Asked Questions about Thousand
What is the value of 1,000 in the decimal system?
In the decimal system, 1,000 is equivalent to 103, which means it’s 10 raised to the power of 3, or 10 multiplied by itself three times, resulting in 1,000 (10 × 10 × 10 = 1,000).
What is the importance of “K” when used with numbers like 5K or 10K?
“K” is an abbreviation for thousand. So, when you see numbers like 5K or 10K, they represent 5,000 and 10,000, respectively.
Does K mean thousand?
Yes, in the context of numbers and units, the “K” is often used as an abbreviation for “thousand.” For example, when you see “$10k,” it represents ten thousand dollars, and when you see “5kW,” it represents five thousand watts.
How do you write one thousand in numbers?
A thousand can be written as 1,000. It is also written as 1000 in some notations, skipping the comma.
What is the face value of each digit in 1,000?
In the decimal system, the “face value” of a digit in a number refers to the actual value represented by that digit based on its position in the number. The face value of the digit “1” in the thousands place is 1. The face value of all the other digits (the three zeros) is 0.
What is the prime factorization of 1,000?
Prime factorization of a number is a way of writing a number as the product of its prime factors. The prime factorization of 1000 is 23 × 53.
Is it three thousand or three thousands?
The correct word form of 3,000 is three thousand. When “thousand” is used to indicate a specific number, it remains in its singular form.