Thousandths

Introduction: What Are Thousandths?

Decimal numbers have a whole number part and a fractional part (or a decimal part) separated by a decimal point. All digits to the right of the decimal point, which represent the fractional part, are decimal digits. The third place from the decimal point is the ‘thousandths’ place. 

For example, 123.456 is a decimal number in which 123 is the whole number and 4, 5, and 6 are decimal digits representing the fractional part. Based on the number of decimal digits, decimal numbers can be named easily. Thousandths are decimals with three decimal digits.

Thousandths Definition

The definition of thousandths can be given as: 

Thousandths is the third place after the decimal point. The decimals that have three decimal digits are also referred to as thousandths.

Examples of thousandths: 0.005, 1.345, 56.789

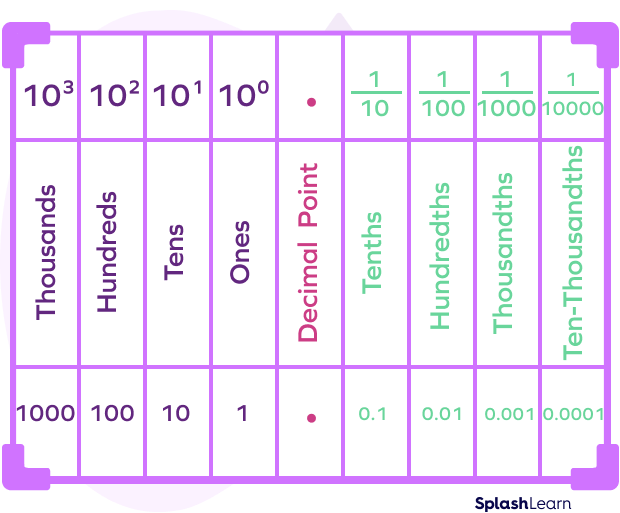
Decimals Place Value Chart

In decimal place values, the thousandths place refers to the third place after the decimal point. It is between the hundredths place and the ten-thousandths place, as shown in the place value chart below.

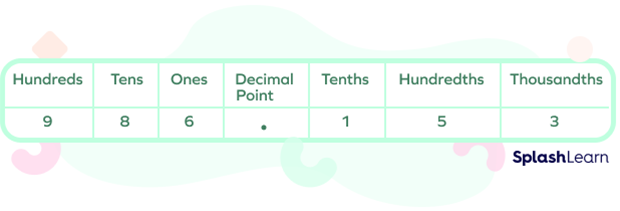
For example, the decimal number 986.153 in the place value system will be written as: 

Tenths, Hundredths, and Thousandths

To understand the thousandths better, let’s first explore tenths and hundredths.

Tenths

Tenths are decimals with one decimal digit, i.e., they have one digit after the decimal point. The decimal 0.5, equal to $\frac{5}{10}$, is pronounced as “five tenths” or “zero point five.”

Hundredths

Hundredths have two digits after the decimal point. The decimal 7.15, equal to $\frac{715}{100}$, is   pronounced as “Seven and fifteen hundredths” or “Seven point fifteen.”

Thousandths

By this time, you could have guessed the meaning of thousandths. It follows a similar pattern. Thousandths have three digits after the decimal point. The decimal, 8.123, equal to $\frac{8123}{1000}$, is pronounced as “Eight and one hundred twenty-three thousandths” or “Eight point one two three.”

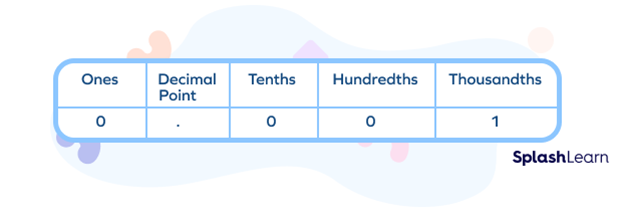
Visual Representation of One Thousandth

One thousandth means one part in a thousand equal parts. The decimal form is 0.001. The fraction form  is $\frac{1}{1000}$.  

Representing Thousandths using Base Ten Blocks

If a large cube is divided into 1000 equal cubes, each small cube will represent one-thousandth of the whole. 

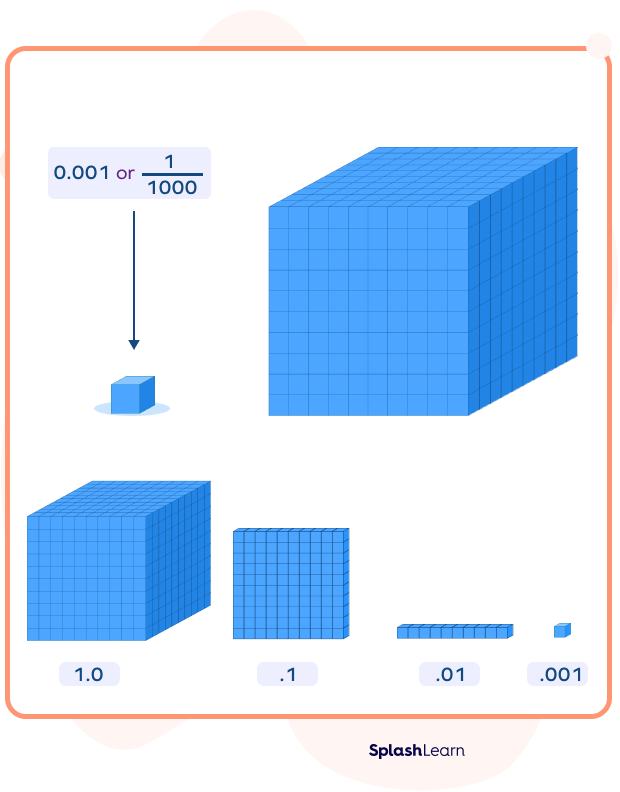
One thousandth $= \frac{1}{1000}$, which in decimal form is equal to 0.001

This image shows the tenth, hundredth, and thousandth part of the large cube. We can represent any decimal number using these parts.

For example: 2.364 has 2 wholes, 3 tenths, 6 hundredths, and 4 thousandths.

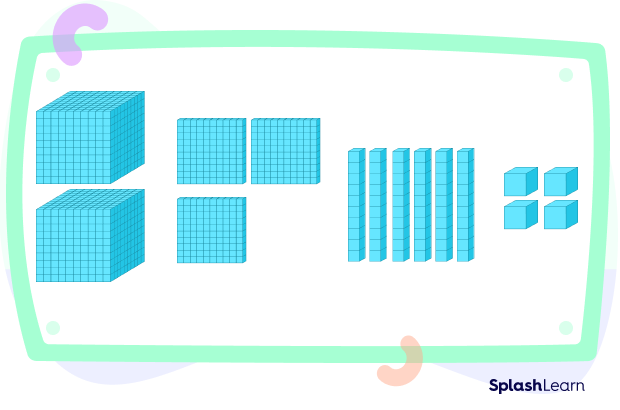
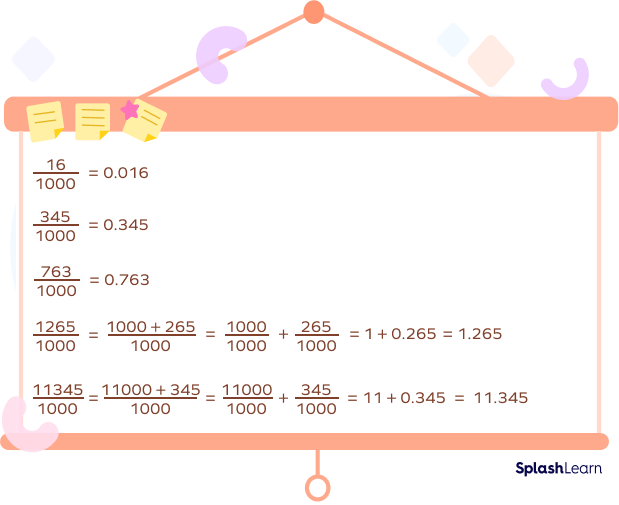
Fractions with 1000 as a Denominator

Fractions with 1000 as denominator can be easily expressed as thousandths. Few points must be considered while writing fractions as thousandths. Three rightmost digits are available to post the decimal point from a fraction of form Number $\frac{1}{1000}$. If we are short of digits, we add zeros at the left of the number.

For instance, $\frac{17}{1000}$ is written as 0.017. Refer to the image given below for similar cases.

Representing Thousandths on a Number Line

Number lines are the horizontal straight lines where the integers are placed in equal intervals.

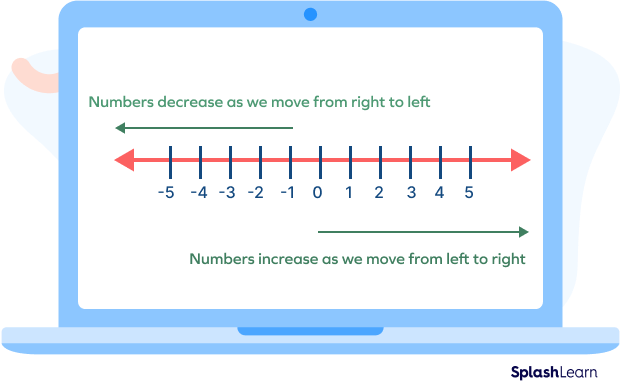
Let’s consider a few examples to understand how to represent decimals on a number line. To represent 7.4, we divide the distance between 7 and 8 into 10 equal parts and select the fourth marking. Each small part equals 0.1.

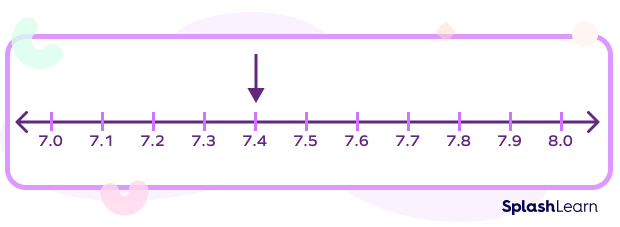
Similarly, to represent 7.45 on a number line, we divide the distance between 7.4 and 7.5 into 10 equal parts and choose the marking for the fifth part. Each small part equals 0.01.

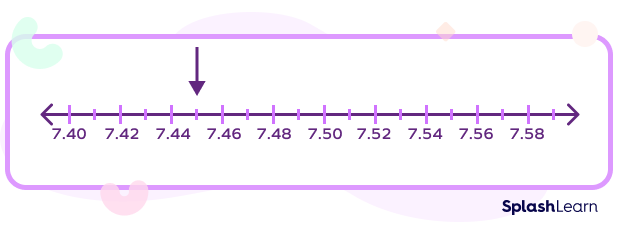
Similarly, to represent 7.456 on a number line, we first divide the distance between 7.45 and 7.46 into 10 equal parts and select the sixth marking. Each small part equals 0.001.

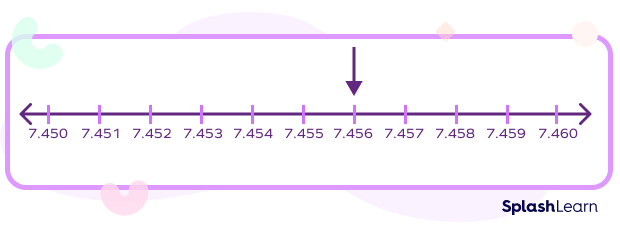
Following are the key points to represent thousandths on a number line.

• Dividing the distance between two whole numbers into 10 equal parts to represent tenths values. 
• Divide the distance between two-tenths again to represent the hundredths values.
• Divide the distance between two-hundredths into 10 equal parts to represent the thousandths values.

‘Thousandth’ as an Ordinal Number

An ordinal number is a number used to indicate an order or position in a list. Thousandth, as an ordinal number, is written as “1000th”. It’s an ordinal number since it also represents a position. 

Example: Suppose you are counting pages of a book. The page that comes after page number 999 will be the 1000th page.

Fun Facts

1. While writing the numbers 0 to 1000 in the word form, the letter “a” appears once in one thousand times!

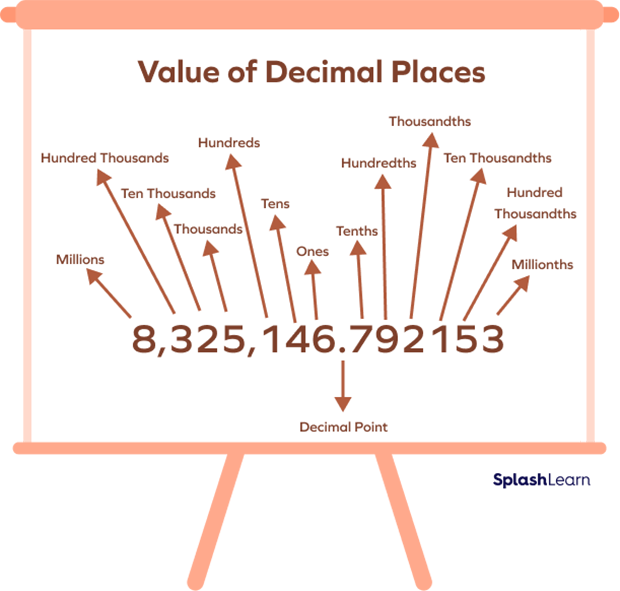
2) The image below will help you understand the place values of a large decimal number before and after the decimal point.

Solved Examples

1. Write 0.597 in words.

Solution: 0.597 is a decimal with three digits post the decimal point. Therefore, we must read the given decimal number until its thousandth part. “Zero point Five Nine Seven.”

Another way to read the given decimal number is “Five Hundred and Ninety-Seven Thousandth”.

2. Identify the digit at the thousandths place in $\frac{825}{1000}$. 

Solution:  $\frac{8}{10}+ \frac{2}{100}+\frac{5}{1000}= \frac{825}{1000}$

So, $\frac{825}{1000} = 0.825$ and the digit at the thousandth’s place comes three positions after the decimal point, which is 5.

3. Write the following as a decimal number. $\frac{2}{10}+ \frac{3}{100}+\frac{7}{1000}$

Solution: $\frac{2}{10}$ can be written as 0.2. 

$\frac{3}{100}$ can be written as 0.03.

Similarly, $\frac{7}{1000}$ can be written as 0.007.

Therefore, $0.2 + 0.03 + 0.007 = 0.237$

Practice Problems

Frequently Asked Questions