Properties of a Kite: Definition, Examples, Facts, FAQs

What Are the Properties of a Kite?

Properties of a kite are the distinct characteristics or features of the kite shape, its vertices, interior angles, sides, diagonals that makes it a unique shape. 

You’re probably familiar with a kite as a fun paper toy that soars high in the sky wherever the wind carries it. The kite is constructed based on a geometrical shape called a “kite.”  Let’s explore the definition of kite and its properties in geometry.

What Is a Kite Shape?

A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent (equal in length). Its diagonals meet at right angles. 

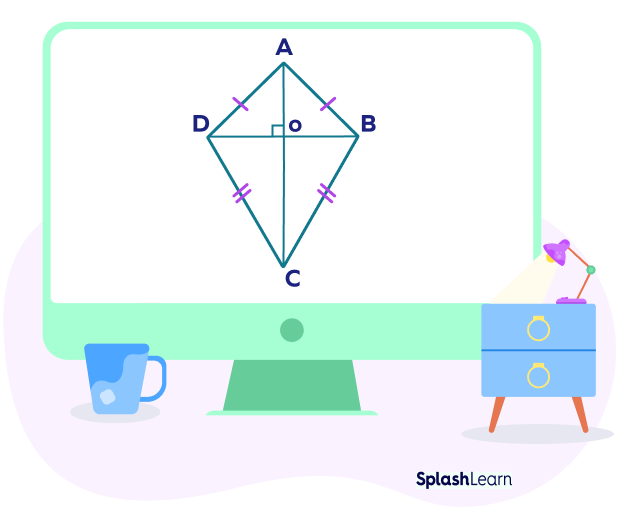
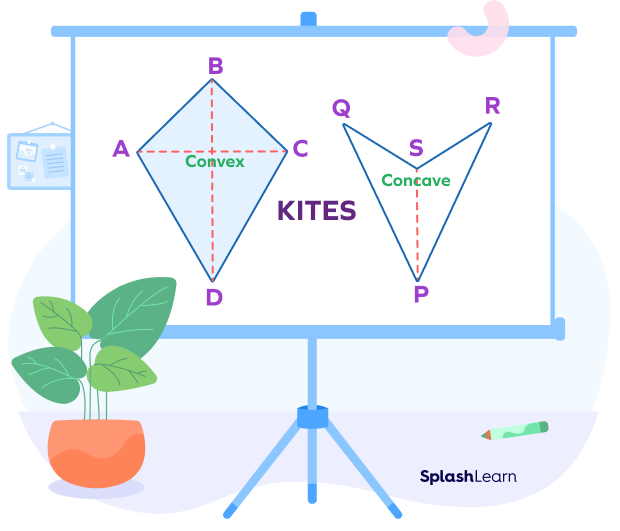
There are two types of kites.

Convex: Each interior angle measures less than $180^\circ$.

Concave: One interior angle is greater than $180^\circ$. A dart or an arrowhead is an example of a concave kite.

Properties of a Kite

Let’s learn the important properties of a kite in geometry using the following diagram. We will discuss side properties of a kite as well as diagonal properties of a kite.

Here, the longer diagonal RS is referred to as the main or primary diagonal.

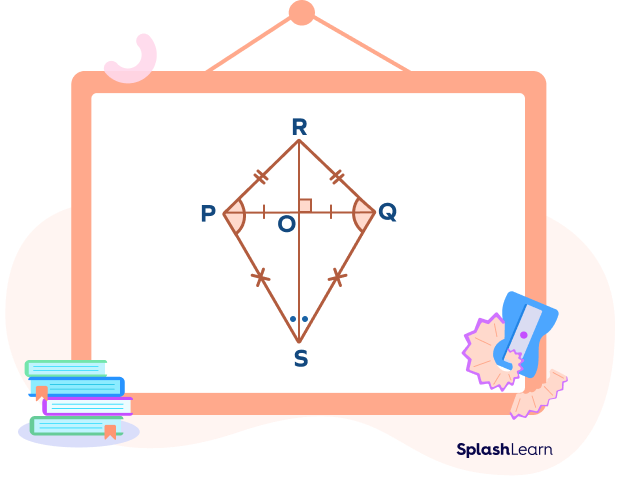
1. Two pairs of adjacent sides are equal. $\left[ PR = QR,\; PS = QS \right]$
2. Two diagonals intersect each other at right angles. $\left[ PQ \;\bot\; RS \right]$
3. The kite is symmetrical about the longer diagonal. 
4. The longer diagonal bisects the shorter diagonal. $\left[ OP = OQ \right]$
5. The angles opposite to the main diagonal are equal. $\left[\angle P = \angle Q\right]$
6. The kite is split into two isosceles triangles by the shorter diagonal.

$[\Delta PRQ \;and\; \Delta PSQ]$

7. The kite is divided into two congruent triangles by the longer diagonal.

$[\Delta PRS \;and\; Delta QRS]$

8. The longer diagonal bisects the pair of opposite angles. 

$\left[\angle PRS = \angle QRS, \;and\; \angle PSR = \angle QSR\right]$

9. The area of kite $= \frac{1}{2} \times d_1 \times d_2$, where $d_1,\; d_2$ are lengths of diagonals.
10. Perimeter of a kite with sides a and b is given by $2\left[a+b\right]$.
11. The sum of the interior angles of a kite $= 360^\circ$.

Properties of Diagonals of a Kite

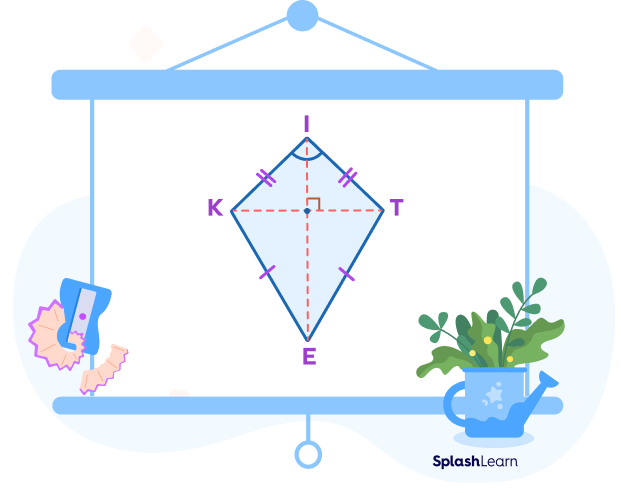
1. Two diagonals of the kite are perpendicular to each other. Thus, KT and IE intersect at right angles. 
2. They are not equal in length.  $\left[KT\; IE\right]$
3. The longer diagonal bisects the shorter diagonal. $\left[OK = OT\right]$
4. Angles opposite to the longer diagonal are congruent. $\left[\angle K = \angle T\right]$

Fun Facts About Properties of a Kite!

• When all the sides of a kite are congruent, it becomes a rhombus.
• Kite is referred to as a dart when it’s not convex. 
• When all sides are congruent and all interior angles measure 90 degrees, the kite becomes a square.
• A kite has all the properties of a cyclic quadrilateral. 
• The product of a kite’s diagonals is equal to half of its area. 

Conclusion

A kite is a quadrilateral form with two pairs of adjacent sides that are congruent. Let’s solve a few examples for better understanding.

Solved Examples on Properties of a Kite

1. Find the area of a kite whose diagonals are 6 and 18 inches long. 

Solution:

Area of a kite $= \frac{d_1\;d_2}{2}$

$= \frac{(6\times18)}{2}$

$= 54$ square inches. 

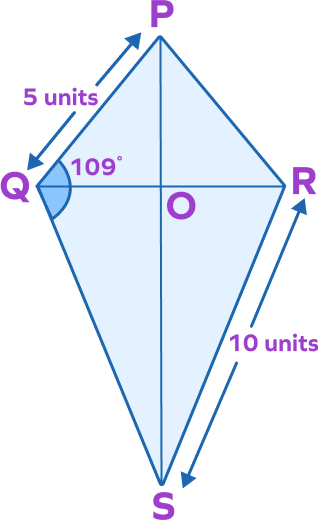
2. Find: 

a) PR 

b) RS 

c) $\angle C$

Solution:

1. Two pairs of adjacent sides of a kite are equal. In the kite PQRS, $PQ = PR \;and\; QS = RS$. 

Since $PQ = 5$ units, $PR = 5$ units.

2. Similarly, $RS = QS = 10$ units
3. Angles opposite to the main diagonal are equal. $\angle C = \angle B = 109^\circ$

3. Four friends are flying identical-sized kites at a park. Each kite has diagonals of 12 inches and 15 inches. Find the total area of four kites combined together. 

Solution:

Lengths of diagonals are:

$d_1 = 12$ in

$d_2 = 15$ in

The area of each kite is:

$A = \frac{1}{2} \times d_1 \times d_2$

    $= \frac{1}{2} \times 12 \times 15$

    $= 90 \;in^2$

Since each kite is the same size, their combined area is equal to $4\times90 = 360 \;in^2$. 

The four kites’ combined surface area is $360 \;in^2$. 

4. Mike wants to offer his pal a kite-shaped chocolate box. He plans to cover the box’s top with a photo of himself and his friend. Find the area of the box’s top if the lid’s diagonals are 9 in and 12 in. 

Solution:

d₁=9 in

d₂=12 in

The area of the box’s top is equal to since the box is shaped like a kite. 

$A = \frac{1}{2} \times d_1 \times d_2$

$A = \frac{1}{2} \times 9 \times 12$

Thus, the box’s top surface area is $54\;in^2$

5. Find the unknown angles of the given kite.

Given that:

$\angle JKL = 130^\circ$

$\angle JML = 50^\circ$

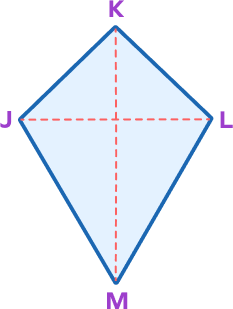
Angles opposite to the main diagonal are congruent.

$\angle KJM = \angle KLM$

Hence, $\angle KLM = 130^\circ$

The sum of all angles of the quadrilateral $= 360^\circ$.

$130^\circ + 130^\circ + 50^\circ + \angle JML = 360^\circ$

$\angle JML = 50$

Practice Problems on Properties of a Kite

Frequently Asked Questions on Properties of a Kite