What Is the Reciprocal Formula?
The reciprocal formula calculates the reciprocal of a given number. The reciprocal of a non-zero number “a” is “1 divided by a.” It is expressed as $\frac{1}{a}$ and represents the multiplicative inverse of the number. In other words, when a number and its reciprocal are multiplied together, the result is 1.
Reciprocal is defined as the multiplicative inverse of a number. If ‘n’ is any non-zero number, the reciprocal will be $\frac{1}{n}$. This means we have to convert the original number to the upside-down form. If the number is multiplied by its reciprocal, the product is equal to one.
Recommended Games
Reciprocal Formula
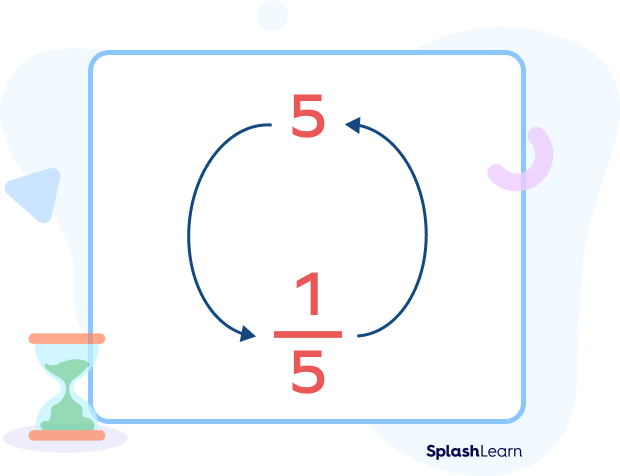
Reciprocal of a non-zero real number $= \frac{1}{Number}$
How to Find Reciprocal
To find the reciprocal of a number, just flip its fraction form.
Example 1: Find the reciprocal of 7.
The given number is 7. In fraction form, we can write it as $\frac{7}{1}$.
Flipping $\frac{7}{1}$ (interchanging the numerator and denominator), we get $\frac{1}{7}$.
Thus, the reciprocal of 7 will be $\frac{1}{7}$.
Similarly, the reciprocal of a fraction can be written by interchanging the values of the numerator and the denominator.
Example 2: Find the reciprocal of $\frac{5}{3}$.
To find the answers, follow the below steps:
Reciprocal formula: $x = \frac{1}{x}$
Here, $x = \frac{5}{3}$
Reciprocal of $\frac{5}{3} = \frac{1}{\frac{5}{3}} = \frac{3}{5}$.
Thus, the reciprocal of the fraction $\frac{5}{3} = \frac{3}{5}$.
Facts about the Reciprocal Formula
- Except zero, all the numbers have reciprocal.
- On multiplying a number and its reciprocal, the product is always one.
- In mathematics, the term “reciprocal” is often used to describe the multiplicative inverse of a number.
- The reciprocal of -1 is -1.
- The reciprocal of 1 is 1.
- Reciprocal of a proper fraction is an improper fraction, and vice-versa.
Conclusion
In this article, we explored the concept of reciprocals and how they are obtained by flipping the fraction form of a number. Understanding reciprocals is essential in various mathematical applications. To reinforce our understanding, let’s work through some examples and test our knowledge with practice MCQs.
Solved Examples on the Reciprocal Formula
Example 1: What is the reciprocal of 5 and 8?
Solution:
The given numbers are 5 and 8. To find the solution, we have to use reciprocal formula:
Reciprocal formula: Reciprocal of $x = \frac{1}{x}$.
Reciprocal of $5 = \frac{1}{5}$
Reciprocal of $8 = \frac{1}{8}$
Thus, the reciprocal of 5 is, $\frac{1}{5}$ and the reciprocal of 8 is $\frac{1}{8}$.
Example 2: What is the reciprocal of $\frac{7}{2}$?
Solution:
The given fraction is $\frac{7}{2}$ . To find the solution, we have to use the reciprocal formula:
Reciprocal formula: Reciprocal of $x = \frac{1}{x}$
Here, $x = \frac{7}{2}$
Reciprocal of $\frac{7}{2} = \frac{1}{\frac{7}{2}} = \frac{2}{7}$.
Thus, the reciprocal of the fraction $\frac{7}{2} = \frac{2}{7}$.
Example 3: Find the reciprocal of $-\;\frac{1}{3}$.
Solution:
The given fraction is $-\;\frac{1}{3}$ . To find the solution, we have to use the reciprocal formula:
Reciprocal formula: Reciprocal of $x = \frac{1}{x}$.
Here, $x = -\;\frac{1}{3}$
Reciprocal of $\frac{-\;1}{3} = \frac{1}{-\;\frac{1}{3}} = -\;\frac{3}{1}$
Thus, the reciprocal of the fraction $-\;\frac{1}{3}$ is $-\;3$.
Practice Problems on the Reciprocal Formula
Reciprocal Formula - Definition, Examples, Practice Problems, FAQs
What is the reciprocal of 6 and $\frac{1}{6}$?
Reciprocal of $6 = \frac{1}{6}$
Reciprocal of $\frac{1}{6} = 6$
What is the reciprocal of $\frac{5}{2}$?
The given fraction is $\frac{5}{2}$ . To find the solution, we have to use the reciprocal formula:
Reciprocal of $x = \frac{1}{x}$.
Here, $x = \frac{5}{2}$
Reciprocal of $\frac{5}{2} = \frac{1}{\frac{5}{2}} = \frac{2}{5}$
Find the reciprocal of $-\;\frac{1}{9}$.
Reciprocal formula: Reciprocal of $x = \frac{1}{x}$.
Here, $x = -\;\frac{1}{9}$
Reciprocal of $-\;\frac{1}{9} = \frac{1}{-\;\frac{1}{9}} = -\;\frac{9}{1} = -\;9$
Frequently Asked Questions about the Reciprocal Formula
How to find the reciprocal of a mixed fraction?
To find the reciprocal of a mixed fraction, convert it into an improper fraction. Then take the reciprocal of the improper fraction. For example: $4\frac{3}{2}$ is a mixed fraction. Converting it into an improper fraction will be $4\frac{3}{2} = \frac{11}{2}$. Now, find the reciprocal by interchanging the denominator and numerator $\frac{2}{11}$ . The reciprocal of $4\frac{3}{2}$ is $\frac{2}{11}$ .
What is finding unity?
If the reciprocal of the number is multiplied by itself, the value will result in unity which is one. For example, $2 \times \frac{1}{2} = 1$.
What is the reciprocal of a negative number?
The reciprocal of any negative number -x will be the inverse of the number along with the negative sign $-\frac{1}{x}$ . For example, the reciprocal of -5 will be $-\frac{1}{5}$ .

















