Reciprocal Identities in Trigonometry

What Are Trigonometric Reciprocal Identities? Introduction

The six trigonometric ratios are sine, cosine, tangent, cotangent, secant, cosecant, out of which the three standard trigonometric ratios are sine, cosine, and tangent. The six trigonometric ratios can be grouped in pairs as reciprocals. The reciprocal identities are the reciprocals of these six trigonometric ratios. Note that reciprocal identities are not the same as inverse trigonometric functions.

Reciprocal identities are the reciprocals of the six fundamental trigonometric functions (sine, cosine, tangent, secant, cosecant, and cotangent). 

We know that the reciprocal of a fraction $\frac{a}{b}$ is given by $\frac{b}{a}$. It is obtained by interchanging the values of numerator and denominator. Similarly, we can find the reciprocal of each trigonometric ratio using their definitions.

Example of reciprocal identity: The reciprocal of the sine ratio is cosecant. 

Reciprocal Identities Formulas

Reciprocal identities are used to simplify calculations in various trigonometry problems. The formulas for the six major reciprocal identities are as follows:

• sin x $= \frac{1}{cosec\; x}$
• cos x $= \frac{1}{sec\; x}$
• tan x $= \frac{1}{cot\; x}$
• cot x $= \frac{1}{tan\; x}$
• sec x $= \frac{1}{cos\; x}$
• cosec x $= \frac{1}{sin\; x}$

Proof of Reciprocal Identities

In geometry, trigonometry is a branch of mathematics that studies the relationship between the sides and angles of a right-angled triangle. Consider a right triangle.

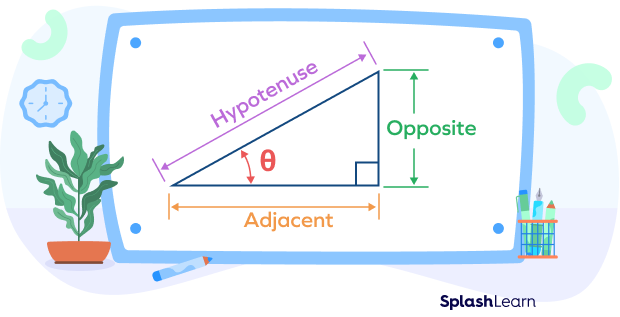
Let’s understand the definition of each trigonometric ratio.

• $sin\; \theta = \frac{Opposite\; Side}{Hypotenuse}$
  $cosec\; \theta = \frac{Hypotenuse}{Opposite\; Side}$
  sine and cosecant are reciprocals.
  Thus, $\frac{1}{sin\; \theta} = cosec\; \theta$  and $\frac{1}{cosec\; \theta} = sin\; \theta$

• $cos\; \theta = \frac{Adjacent\; Side}{Hypotenuse}$
  $sec\; \theta = \frac{Hypotenuse}{Adjacent\; Side}$
  cosine and secant are reciprocals.
  Thus, $\frac{1}{cos\; \theta} = sec\; \theta$  and $\frac{1}{sec\; \theta} = cos\; \theta$

• $tan\; \theta = \frac{Opposite\; Side}{Adjacent\; Side}$
  $cot\; \theta = \frac{Adjacent\; Side}{Opposite\; Side}$
  tangent and cotangent are reciprocals.
  Thus, $\frac{1}{tan\; \theta} = cot\; \theta$  and $\frac{1}{cot\; \theta} = tan\; \theta$

In summary:

• sin $\theta$ is the reciprocal of cosec $\theta$.
• cosec $\theta$ is the reciprocal of sin $\theta$.
• cos $\theta$ is the reciprocal of sec $\theta$.
• sec $\theta$ is the reciprocal of cos $\theta$.
• tan $\theta$ is the reciprocal of cot $\theta$.
• cot $\theta$ is the reciprocal of tan $\theta$.

Relationship between Reciprocal Identities

We know that any number multiplied with its reciprocal results in 1. Similarly, the product of a trigonometric ratio and its reciprocal is one. 

• $sin\; \theta \times csc\; \theta = 1$
• $cos\; \theta \times sec\; \theta = 1$
• $tan\; \theta \times cot\; \theta = 1$

Note:

 $tan\; \theta = \frac{sin\; \theta}{cos\; \theta}$

$cot\; \theta = \frac{cos\; \theta}{sin\; \theta}$

Conclusion

Reciprocal identities are the reciprocals of the six fundamental trigonometric functions (sine, cosine, tangent, secant, cosecant, and cotangent). In this article, we explored different reciprocal identities, their formulas, and proof. Let’s solve a few examples and practice problems.

Solved Examples on Reciprocal Identities

1. With the use of a reciprocal identity, determine the expression’s value.

$\frac{sin\; \theta}{cos\; \theta} \times sec\; \theta \times csc\; \theta$

Solution:

We know that,

$csc\; \theta = \frac{1}{sin\; \theta}$ and $sec\; \theta = \frac{1}{cos\; \theta}$

Substituting these values, 

$\frac{sin\;\theta}{cos\;\theta} \times sec\;\theta \times csc\;\theta = \frac{sin\;\theta}{cos\;\theta} \times \frac{1}{cos\;\theta} \times \frac{1}{sin\;\theta}$

$= \frac{1}{cos\;\theta} \times \frac{1}{cos\;\theta}$

$= \frac{1}{cos^{2}\theta}$

$= sec^{2}\theta$

2. If sin x $=\frac{1}{2}$ and cos x $= \frac{\sqrt{3}}{2}$, find all the other trigonometric ratios.

Solution:

sin x $= \frac{1}{2}$

cos x $= \frac{\sqrt{3}}{2}$

tan x $= \frac{sin\;\theta}{cos\;\theta} = \frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} = \frac{1}{\sqrt{3}}$

cosec x $= \frac{1}{sin\; x} = 2$

sec x $= \frac{1}{cos\; x} = \frac{2}{sqrt{3}}$

3. For $\theta = 90^{\circ}$, sin $\theta = 1$ and cos $\theta = 0$. Find cosec $\theta$ and sec $\theta$.

Solution:

$sin\; \theta = 1,\; cos\; \theta = 0$

$cosec\;\theta = \frac{1}{sin\;\theta}$ and$sec\;\theta = \frac{1}{cos\;\theta}$

$cosec\;\theta = \frac{1}{1}$ and $sec\;\theta = \frac{1}{0}$

$cosec\;\theta = 1$ and $sec\;\theta = Not\; defined$

Practice Problems on Reciprocal Identities

Frequently Asked Questions on Reciprocal Identities