What Is the Volume of a Rectangular Pyramid?
A rectangular pyramid is a three dimensional object with a rectangle as its base and triangular lateral faces. A rectangular pyramid is crowned at the top at a point known as the apex. Except for the base, all the faces connect at a vertex at the top called the apex.
Thus, a rectangular pyramid has these main parts: a rectangular base, four triangular faces, five vertices, and eight edges.
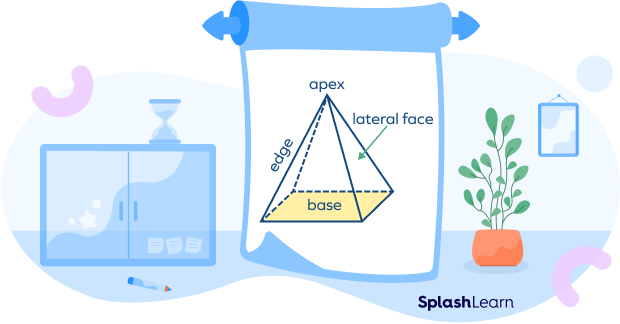
Depending on the position of the axis of the rectangular pyramid, it is classified into two types.
- Right rectangular pyramid: The apex is aligned with the center of the base.
- Oblique rectangular pyramid: The apex is not aligned with the center of the base. The perpendicular line drawn from the apex to the base of the pyramid determines the height of the oblique rectangular pyramid.
The amount of unit cubes that can fit within a rectangular pyramid is called its volume. The volume is measured in cubic units. For example, it can be expressed as $in^{3},\; ft^{3},\; unit^{3}$, etc., depending upon the given units. The general formula to calculate the volume of a pyramid is equal to one-third the product of the area of the base and the height of the pyramid.
Recommended Games
Volume of Rectangular Pyramid Formula
The volume of a rectangular pyramid depends on the area of the base and its height. It is measured in cubic units. The formula for the volume of the rectangular pyramid is as follows:
Volume $= \frac{1}{3}\times$ Base Area$\times$ Height
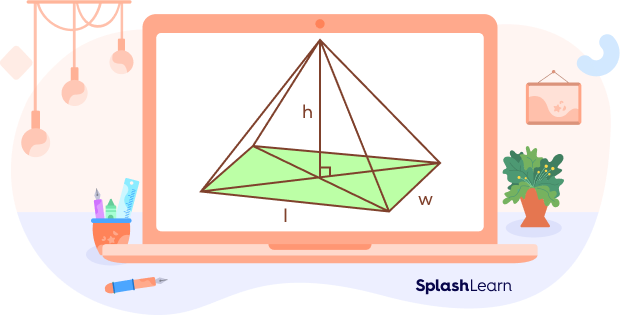
Here,
l $=$ length of the rectangular base
w $=$ width of the rectangular
h $=$ perpendicular height of rectangular pyramid
Base area of the rectangular pyramid $=$ Area of rectangle $=$ Length $\times$ Width $= l \times w$
Thus,
Volume of rectangular pyramid $= \frac{1}{3} \times $length $\times$width $\times$ height $= \frac{1}{3} \times$ l $\times$ w $\times$ h
Recommended Worksheets
How to Find the Volume of a Rectangular Pyramid
The volume of a rectangular pyramid is calculated using the formula:
Volume $= \frac{1}{3} \times$ Base Area $\times$ Height $= \frac{1}{3} \times$ l $\times$ w $\times$ h
Let’s look at the steps to find the volume of a rectangular pyramid.
Step 1: Find the area of the base of the pyramid using the formula of area of rectangle.
Area of the base $=$ Length $\times$ Breadth
Step 2: Find the volume using the formula: Volume $= \frac{1}{3} \times $ Base Area $\times$ Height
Step 3: The volume is expressed in cubic units, like $in^{3},\; ft^{3},\; unit^{3}$, etc.
Fun Facts!
- The rectangular pyramid is one of the most common pyramids we encounter the first time we learn about three-dimensional figures.
- A rectangular pyramid is a three-dimensional figure that has triangles as surfaces and a rectangle as its base.
- The volume of a rectangular pyramid is simply equal to the amount of space that can be occupied within the rectangular pyramid.
- The volume of a rectangular pyramid is a third of the corresponding rectangular prism.
- Three rectangular-based pyramids fill one rectangular cuboid (with the same size base and height).
Conclusion
In this article, we learned the definition, meaning, and formula of the volume of a rectangular pyramid. Let’s solve some examples to understand it better.
Solved Examples
1. Determine the volume of a rectangular pyramid shaped tank whose base area and height are $60\; ft^{2}$ and 10 ft respectively.
Solution:
Area of the rectangular base $= 60\; ft^{2}$
The height of the pyramid shaped tank $= 10\; ft$
We know that,
The volume of the rectangular pyramid (V) $= \frac{1}{3} \times$ Base Area $\times$ Height
$= \frac{1}{3} \times60 \times10$
$= 20 \times 10$
$= 200\; ft^{3}$
Hence, the volume of the given rectangular pyramid shaped tank is $200\; ft^{3}$.
2. Find the volume of a rectangular pyramid if the base length is 10 inches and the base width is 6 inches, and the height of the pyramid is 14 inches.
Solution:
Base length (l) $= 10$ inches
Base width (w) $= 6$ inches
The height of the pyramid (h) $= 14$ inches
We know that,
Base area of rectangular pyramid $=$ length $\times$ width
$= 10 \times 6$
$= 60\; in^{2}$
Now, The volume of the rectangular pyramid (V) $= \frac{1}{3} \times$ Base Area $\times$ Height
$= \frac{1}{3} \times 60 \times 14$
$= 13 \times 840$
$= 280\; in^{3}$
Hence, the volume of the given rectangular pyramid is $280\; in^{3}$.
3. Determine the height of a rectangular pyramid whose base area and volume are 120 $ft^{2}$ and 360 $ft^{3}$, respectively.
Solution:
Area of the rectangular base $= 120\; ft^{2}$
The volume of the rectangular pyramid $= 360\; ft^{3}$
We know that,
The volume of the rectangular pyramid (V) $= \frac{1}{3} \times$ Base Area $\times$ Height
$360 = \frac{1}{3} \times 120 \times$ Height
$360 = 40 \times$ h
h $= \frac{360}{40}$
$= 9$ ft.
Hence, the height of the given rectangular pyramid is 9 ft.
4. The base of rectangular pyramid has a dimension of $8\; ft \times 10\;ft$ and its height is 12 ft. What is the volume of the rectangular pyramid?
Solution:
h $= 12$ inches.
The base area $= 8 \times 10 = 80\; ft^{2}$.
The volume of the rectangular pyramid (V) $= \frac{1}{3} \times$ Base Area $\times$ Height
$= \frac{1}{3} \times (80) \times 12$
$= \frac{960}{3}$
$= 320\; ft^{3}$
Volume of the given rectangular pyramid $= 320\; ft^{3}$
Practice Problems on Volume of Rectangular Pyramid
Volume of Rectangular Pyramid: Formula, Examples
When the peak or the apex of a rectangular pyramid is not directly above the center of the base, the pyramid is said to be ___________ .
In the right rectangular pyramid, the apex is directly above the center of the base and in the oblique pyramid the apex is not directly above the center.
Which of the following is NOT the unit of measurement of volume?
Volume is expressed in cubic units (3), because it is measured in three dimensions (e.g. length$\times$width$\times$depth) and is expressed as $ft^{3},in^{3},yard^{3}$, etc.
The volume of a rectangular pyramid is found using the formula ___________ .
The formula for the volume of the rectangular pyramid is,
Volume $= \frac{1}{3} \times$ Base Area $\times$ Height
Here, base area of the rectangular pyramid $=$ Length $\times$ Width (as the base is a rectangle)
Thus,
Volume of rectangular pyramid $= \frac{1}{3} \times$ length $\times$ width $\times$ height.
What is the volume of a rectangular pyramid that has a base area of 18 square units and height 4 units?
Volume of rectangular pyramid $= \frac{1}{3} \times$ Base Area $\times$ Height
$= \frac{1}{3}\times18\times4$
$= 24\;unit^{3}$
Frequently Asked Questions on Volume of Rectangular Pyramid
Does the volume of the pyramid change if the type of pyramid changes?
The volume of the pyramid depends on the base area and the height of the pyramid. As the type of pyramid changes, the base of the pyramid changes, thereby changing the base area of the pyramid. Thus, change in the base area of the pyramid changes the volume of the pyramid.
What is the surface area of a rectangular pyramid?
A rectangular pyramid has two types of surface areas, i.e., the lateral surface area and the total surface area.
- The lateral surface area of a rectangular pyramid is equal to the sum of the areas of its four lateral faces, i.e., triangular faces. In a rectangular pyramid, the areas of the opposite triangular faces are the same.
The formula for the lateral surface area of the rectangular pyramid is
LSA $= l\; \sqrt{(\frac{w}{2})^{2} + h^{2}}\;+w\;\sqrt{(\frac{l}{2})^{2} + h^{2}}$
- Total Surface Area of a Rectangular Pyramid $=$ (Area of base) $+$ ( Area of 4 lateral faces)
Here, Area of base $=$ length $\times$ width $= ( l \times w )$, as it is a rectangle. Thus, the formula for total surface area of a rectangular pyramid is as follows:
TSA $= (lw) + l \sqrt{ [(\frac{w}{2})^{2} + h^{2}]} + w\sqrt{[(\frac{l}{2})^{2} + h^{2}]}$ square units.
Why is there a term $\frac{1}{3}$ in the formula for the volume of a pyramid?
A cube of unit length can be divided into three congruent pyramids. Also, it is possible to divide the cuboid into three pyramids of equal volume. It follows that the volume of each pyramid is one-third the volume of the cube/cuboid. Hence, in general, we have the term 13 in the volume of the pyramid.
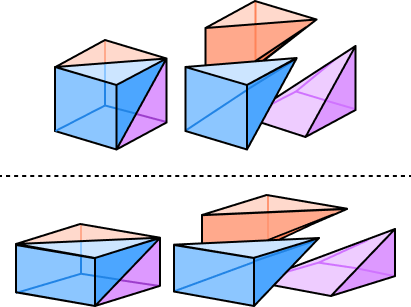
Do all pyramids have the same volume formula?
The volume of a pyramid depends upon its base.
We know that, volume of a pyramid $= \frac{1}{3} \times$ Base Area $\times$ Height.
In case of a rectangular pyramid, base area $=$ Length $\times$ Width
Thus, Volume $= \frac{1}{3}$ length $\times$ width $\times$ height.
In case of a square pyramid, base area $=$ side $\times$ side or $side^{2}$
Thus, Volume $= \frac{1}{3} \times side^{2}\; \times$ height.
Similar formulas can be derived for all the other pyramids.




























