Representation of Irrational Numbers on Number Line – Examples, FAQs

What Is Representation of Irrational Numbers on a Number Line?

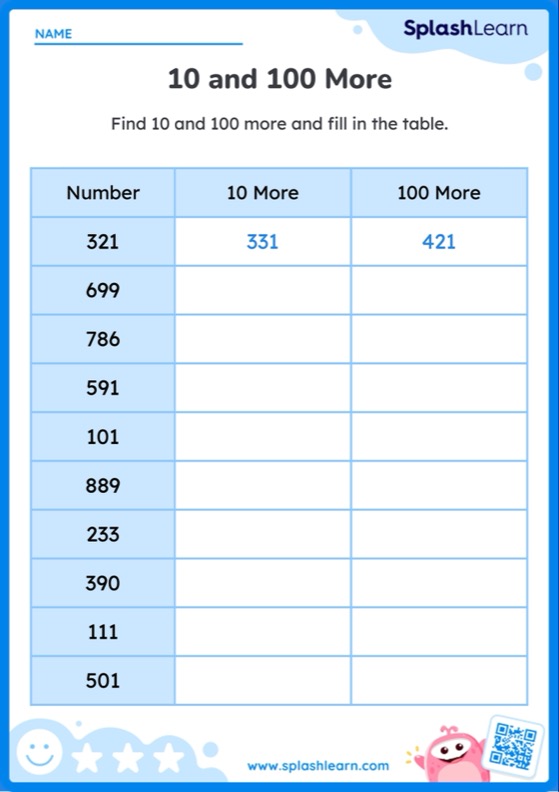
Representation of irrational numbers can be done by using the Pythagorean theorem. We break down the number inside the square root into two equal parts, where each part represents the side of the right triangle that we form. The hypotenuse of the right triangle represents the given irrational number. This length is used to mark the approximate location of the irrational number on the number line.

Alt tag: Irrational numbers on number line – understanding the basics

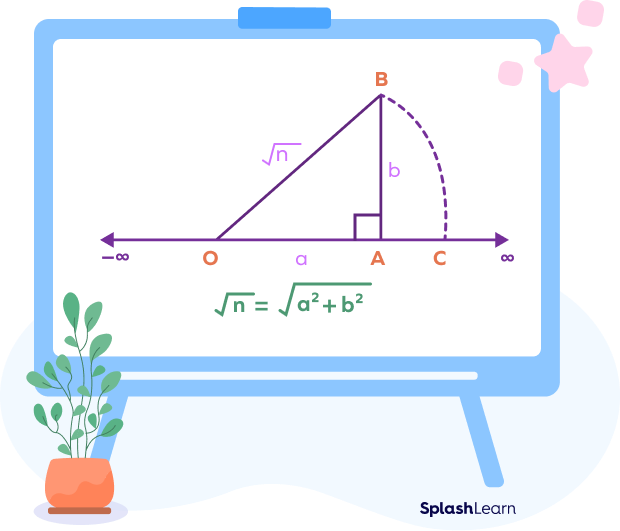
Each and every point on a number line represents a unique real number. We can represent each real number with the help of a unique point on the number line. Irrational numbers and rational numbers together form the set of real numbers.

What Are Irrational Numbers?

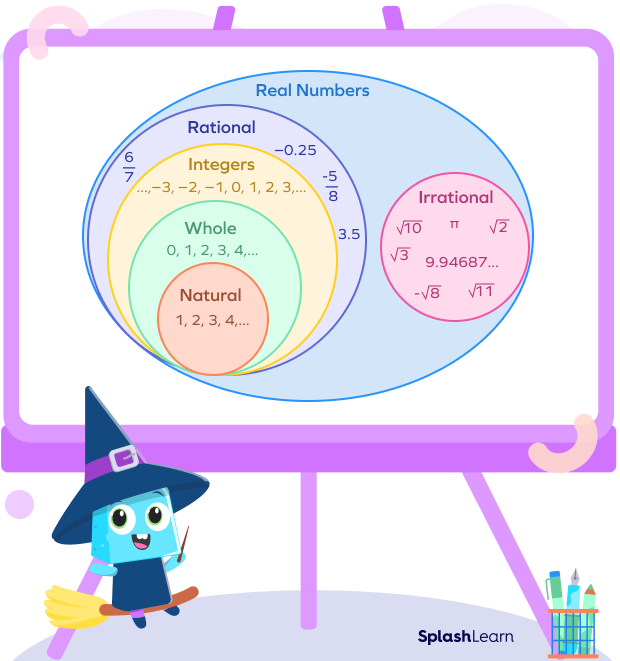
Irrational numbers are the real numbers that cannot be written in the form of a ratio (rational form) $\frac{p}{q}$, where p, q are integers and $q \neq 0$. 

In simple words, all the real numbers that are not rational numbers are irrational. These numbers include non-terminating, non-repeating decimals.

What Is a Number Line?

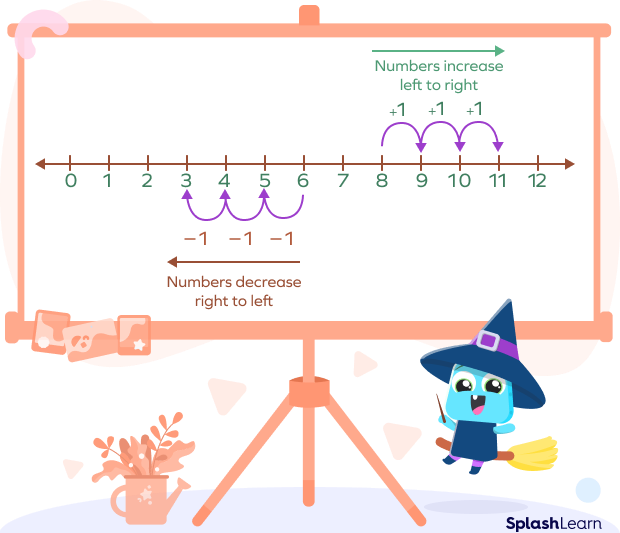
In math, a number line is a pictorial representation of numbers on a straight line (horizontally or vertically). 

• The numbers on a number line are placed sequentially at equal distances along its length. 
• It can be extended infinitely in both directions and is usually represented horizontally. 

• Writing numbers on the number line makes it easier to compare numbers or to perform arithmetic operations on them. 
• Numbers on the right side of 0 are positive. Numbers on the left side of 0 are negative.
• The numbers on a number line increase as one moves from left to right and decrease on moving from right to left. 

How to Represent Irrational Numbers on a Number Line

Irrational numbers in the form of $\sqrt{n}$, where n is a positive integer can be represented on a number line. Keep in mind that irrational numbers cannot be represented precisely on a number line due to their infinite and non-repeating decimal expansions, so we use approximations to visually represent them. 

Let’s see the steps to represent irrational numbers on a number line.

Steps Used to Represent Irrational Numbers on a Number Line

Let’s understand the steps with the help of an example.

Example: Represent $\sqrt{2}$ on a number line

Step 1: Draw a number line. Mark and label integers 0, 1, and -1 as shown below.

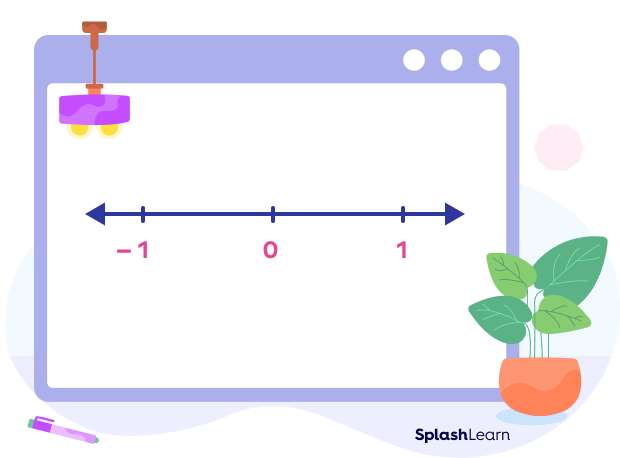
Step 2: We can express $\sqrt{2}$ as $\sqrt{2} = \sqrt{1 + 1}$.

Let the point representing zero be O. 

Let the point representing 1 be B.

Draw a line perpendicular at B such that l(AB)=1 unit.

Step 3: Construct a right-angled triangle OAB by joining OA. 

AB will be the height, OB will be the base, and OA will be the hypotenuse.

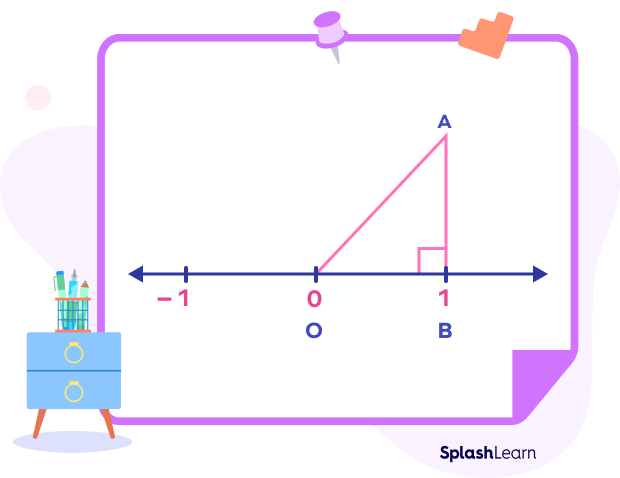
Step 4: Find the length of the hypotenuse by applying the Pythagorean Theorem

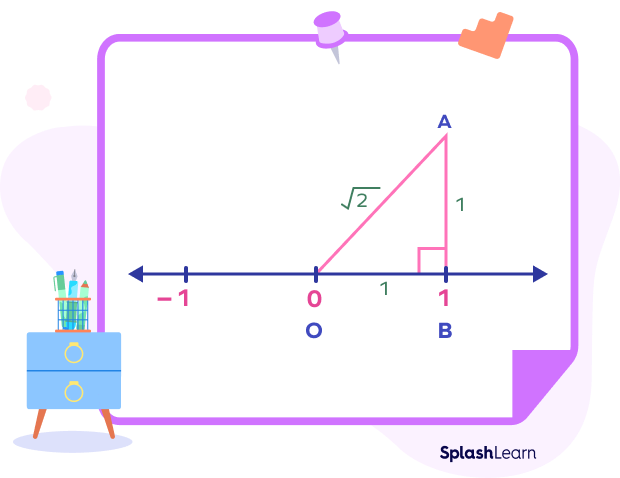
$(OA)^{2} = (AB)^{2} + (BC)^{2}$

$(OA)^{2} = (1)^{2} + (1)^{2}$

$(OA)^{2} =   2$

$OA  = \sqrt{2}$

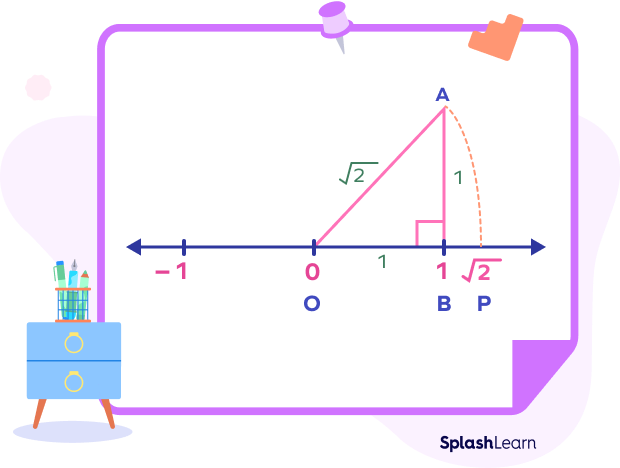
Step 5: Now, keeping OA as radius and O as the center, draw an arc on the number line and name the point as P. Now, the distance OP is equal to $\sqrt{2}$. The point P represents $\sqrt{2}$ on the number line.

Facts about Representation of Irrational Numbers on a Number Line

Conclusion

In this article, we have learned about irrational numbers and how they can be represented on the number line. Irrational numbers are special in a way that though they cannot be expressed fully as fractions, they can be visualized on a number line by using approximations. Now let’s solve some examples and practice problems to understand the concept in a better way!

Solved Examples on Representation of Irrational Numbers on a Number Line

Example 1: Represent 5 on the number line.

Step 1: Draw a number line and mark the points 0, 1, and -1.

Step 2: Draw a line perpendicular at the point 1 in such a way that the perpendicular line segment has a length of 2 units.

Step 3: Construct a right-angled triangle ABC as shown below. AB will be the height, BC will be the base, and AC will be the hypotenuse.

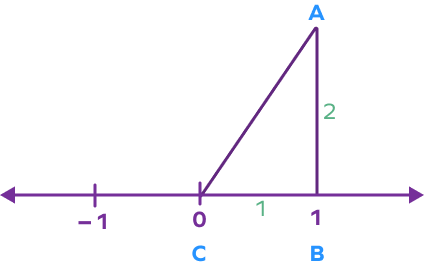
Step 4: Find the length of the hypotenuse by applying the Pythagorean Theorem

$(AC)^{2} = (AB)^{2} + (BC)^{2}$

$(AC)^{2} = (2)^{2} + (1)^{2}$

$(AC)^{2} =  4 + 1$

$AC = \sqrt{5}$

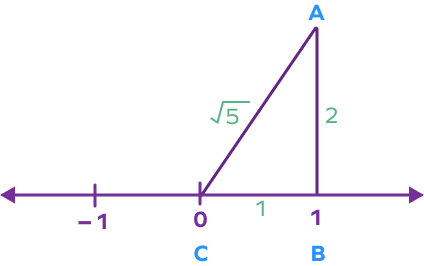
Step 5: Now with AC as radius and C as the center, draw an arc on the number line that cuts the number line at D. Here, CD will represent the distance $\sqrt{5}$.

Thus, the point D represents $\sqrt{5}$ on the number line.

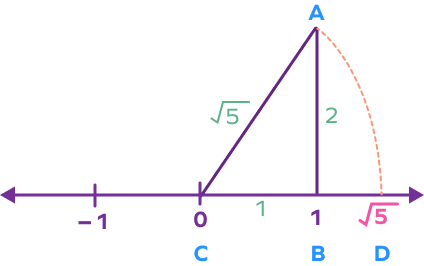
Example 2: Represent 3 on the number line.

Solution: 

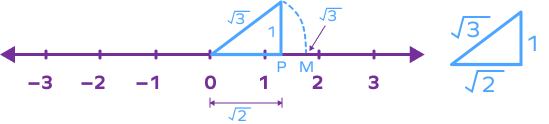
In order to represent $\sqrt{3}$ on the number line, we must first represent $\sqrt{2}$  on the number line. We have already discussed the steps for representing $\sqrt{2}$. Suppose, we mark $\sqrt{2}$ on the number line as shown below using point P.  

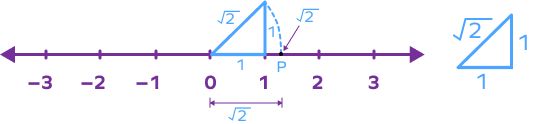
Now, we will use this point P to locate $\sqrt{3}$ on the number line. Take base $= OP = \sqrt{2}$ units. Draw a perpendicular at P of 1 unit length. Using pythagoras theorem, we get

Hypotenuse $= (\sqrt{2})^{2} + (1)^{2} = \sqrt{2 + 1} = \sqrt{3}$

Taking origin as center and hypotenuse as radius, draw an arc that meets the number line at point M. 

The point M represents the irrational number $\sqrt{3}$ on the number line.

Example 3: Represent $\sqrt{7}$ on the number line.

Solution: 

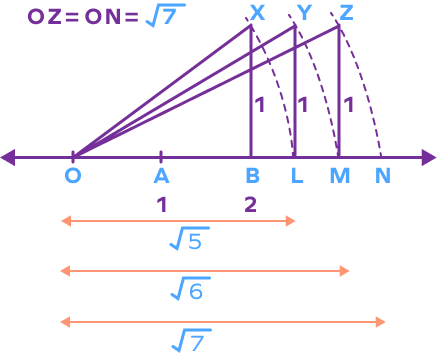
i) We can use $\sqrt{5}$ and $\sqrt{6}$ to represent $\sqrt{7}$ on the number line.

Here, $\sqrt{5} = \sqrt{2^{2} + 1^{1}}$ can be represented by applying Pythagoras theorem in a right triangle with base = 2 units and height 1 unit.

Suppose that the point L represents $\sqrt{5}$.

ii) Next, we can express $\sqrt{6} = \sqrt{(\sqrt{5})^{2} + 1^{1}}$.

To represent $\sqrt{6}$, choose base length $= OL = \sqrt{5}$ units and height = 1 unit. Let point M represent $\sqrt{6}$ on the number line.

iii) Similarly, we can write $\sqrt{7} = \sqrt{(\sqrt{6})^{2} + 1^{1}}$. 

To represent $\sqrt{7}$, choose base = OM = 6 units and height = 1 unit. Draw an arc keeping 0 as center and hypotenuse OZ as radius. Suppose it meets the number line at point N.

Here, OZ = ON = $\sqrt{7}$.

The point N represents $\sqrt{7}$.

Practice Problems on Representation of Irrational Numbers on a Number Line

Frequently Asked Questions about Representation of Irrational Numbers on a Number Line