RHS Congruence Rule – Statement, Proof, Examples, Facts, FAQs

What Is the RHS Congruence Rule in Geometry?

RHS (Right angle-Hypotenuse-Side) congruence criterion is used to prove the congruence of two right-angled triangles. It states that if the hypotenuse and one side (leg) of one right triangle are congruent to the hypotenuse and the corresponding side of the other right triangle, then the two right triangles are congruent.

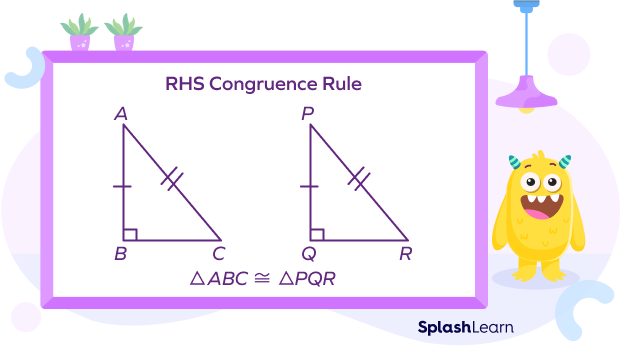
In the diagram shown below, there are two right triangles ▵ABC &  ▵PQR such that 

hypotenuse AC = hypotenuse PR

Side AB = Side PQ

Thus, by RHS congruence criterion, ▵ABC ≅  ▵PQR

The RHS congruence rule is also known as the HL (Hypotenuse-Leg) congruence rule. Note that this theorem is only applicable to the right-angled triangles.

The RHS rule is based on the Pythagoras theorem. In a right triangle, if we know the length of any two sides, we can find the length of the missing side using the Pythagoras theorem, which states that 

Hypotenuse² = Base² + Perpendicular²

Thus, if the hypotenuse and one side of one right triangle are congruent to the hypotenuse and corresponding side of another right triangle, the remaining sides will automatically be equal.

RHS Congruence Rule Statement

The RHS (Right Angle-Hypotenuse-Side) congruence rule states that if the hypotenuse and one side of one right triangle is equal to the hypotenuse and corresponding side of the other right triangle, then the two given right triangles are congruent.

Proof of RHS Congruence Theorem

Given: Two right-angled triangles ABC and  DEF where ∠B=90°  and ∠E=90°.

Hypotenuses are equal. (AC = DF)

One pair of corresponding sides is equal. (BC = EF)

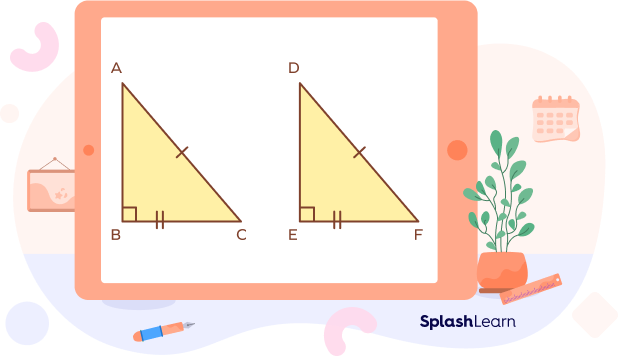
To prove: ΔABC ≅ ΔDEF

Proof:

Statement	Reason
$AC^{2} = AB^{2} + BC^{2}$ $\Rightarrow AB^{2} = AC^{2} – BC^{2}$                           …(1)	Pythagoras theorem in right triangle ABC
$DF^{2} = DE^{2} + EF^{2}$ $\Rightarrow DE^{2} = DF^{2} – EF^{2}$                              …(2)	Pythagoras theorem in right triangle DEF
AC = DF and BC = EF                            …(3)	Given
$AB^{2} = DF^{2} – EF^{2}$                                 …(4)	From (1) and (3)
$AB^{2} = DE^{2}$ $\Rightarrow AB = DE$	From (2) and (4)
In ΔABC and  ΔDEF, AB = DE BC = EF AC = DF	From (3) and (4)
ΔABC ≅ ΔDEF	SSS Congruence Criterion

Conclusion

In this article, we learned about the Right Hand Side (RHS) Congruence Rule and how it is applied. By understanding this rule, we can determine the congruence of two right triangles based on the congruence of their hypotenuse and one corresponding leg. Let’s solidify our understanding by working through examples and practicing MCQs for better comprehension.

Facts about RHS Congruence Rule

Solved Examples on RHS Congruence Theorem

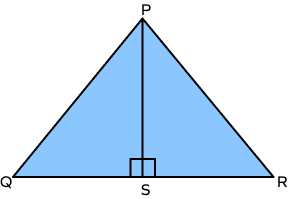
Example 1: In the given figure PQ = PR, ∠PSQ=∠PSR=90°. Prove that  ΔPSQ ≅ ΔPSR

Solution: 

In ΔPSQ and ΔPSR,

PQ = PR (given)

PS = PS (common side)

∠QSP=∠RSP (both right angles)

Hypotenuse and one side of ΔPSQ is congruent to the hypotenuse and the corresponding side of  ΔPSR.

Thus, by RHS rule, ΔPSQ ≅ ΔPSR. Hence proved. 

Example 2: Are the two right triangles ΔABC and ΔPQR congruent by RHS rule?

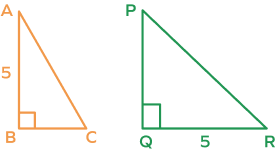
Solution:

To prove that two right triangles ΔABC and ΔPQR are congruent by RHS congruence criterion, the hypotenuse and one side of ΔABC must be congruent to the hypotenuse and the corresponding side of ΔPQR.

Here, it is given that AB = QR and ∠ABC=∠PQR=90. 

However, it is not mentioned that the hypotenuses are equal.

Thus, we cannot say that the two triangles are congruent by RHS congruence rule. The information is not sufficient.

Example 3: Prove the given triangles are congruent.

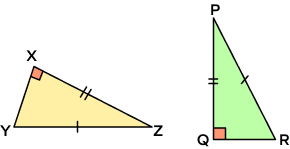
Solution:

In the given triangles, ΔYXZ and ΔPQR,

side XZ = side PQ (given)

Hypotenuse YZ = Hypotenuse PR  (given)

∠YXZ=∠PQR =90° (given)

Hypotenuse and one side of ΔYXZ is congruent to the hypotenuse and the corresponding side of  ΔPQR.

Thus, by RHS theorem, ΔYXZ ≅ ΔPQR. 

Practice Problems on RHS Congruence Theorem

Frequently Asked Questions about RHS Congruence Theorem