Sector of a Circle: Definition, Formula, Area, Perimeter, Examples

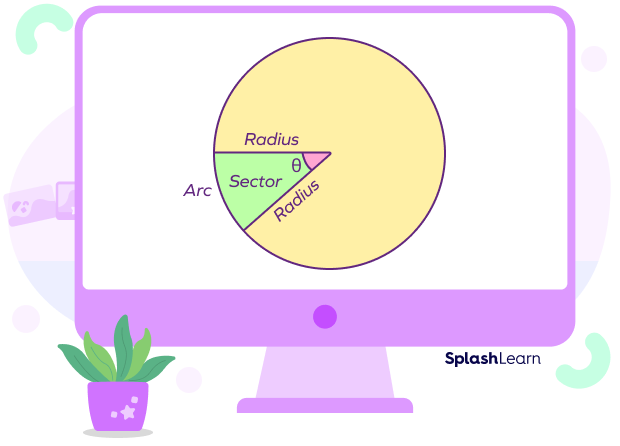
What Is a Sector of a Circle?

A sector of a circle is a portion or part of a circle that is composed of an arc and its two radii. You can compare the sector of a circle to the shape of a pizza slice. A sector is formed when two radii of the circle meet at both ends of the arc. An arc is simply a portion of the circumference of the circle.

Sector of a Circle Definition

The definition of the sector of a circle in geometry can be given as the part of the circle enclosed by two radii and an arc of the circle. The arc of the circle is a part of the boundary/circumference of the circle.

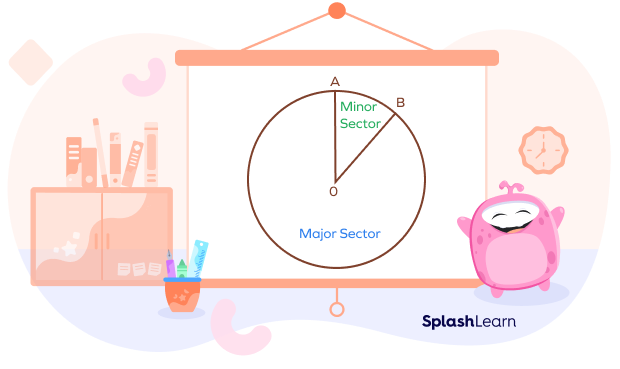
Two radii meet at the center of the circle to form two sectors. 

• Minor sector
• Major sector

Minor Sector

A sector of a circle is called the minor sector if the minor arc of the circle is a part of its boundary. It is the sector with a smaller area. The angle of a minor sector is less than 180 degrees.

Major Sector

A sector is called the major sector if the major arc of the circle is a part of its boundary.

It is the sector with the greater area. The angle of a major sector is greater than 180 degrees.

Sector of a Circle Formulas

Let’s learn how to find the area of a sector of a circle. The formula for determining the area of a sector is given in two ways, with an angle and without an angle. 

Area of a Sector Formula: When Angle Is Given

If the radius of a circle is given as “r” and the angle of the sector is given as . This angle is made by the two radii at the center.

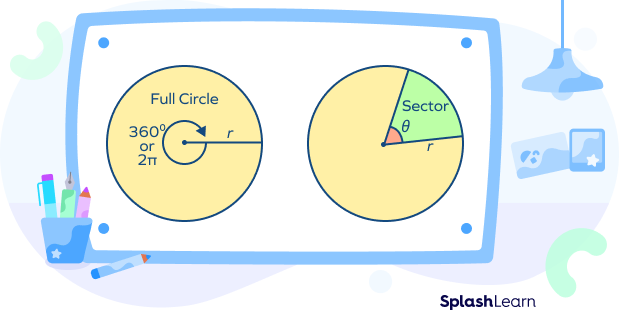
As we know, for a complete circle, the angle made at the center is equal to 2 or $360^\circ$.

• If is measured in degrees, then “the area of a sector of a circle formula” is given by

Area of sector $= \frac{\theta}{360^\circ} \times \pi r^2$

• If is measured in radians, then “the area of a sector of a circle formula” is given by

Area of sector $= \frac{1}{2} \times \theta \times r^2$

• Perimeter of sector $=2r + \frac{\theta}{360} \times 2\pi r$

Area of Sector Formula: When Angle Is Not Given

How can we find the area of a sector of a circle when the central angle is not given? Let’s find out. 

If l is the length of the arc, r is the radius of the circle and θ is the angle subtended at the center, then the angle is expressed in terms of l and r as

$\theta = \frac{l}{r}$, where is in radians.

If the angle of the sector $=2\pi$, the area of the sector (full circle) is $r^2$.

Similarly, for the angle $= 1$, the area of the sector $= \frac{\pi r^2}{2\pi} = \frac{r^2}{2}$

Thus, for the angle , area of the sector $\theta = \frac{r^2}{2} = \frac{l}{r}\times\frac{r^2}{2} = \frac{lr}{2}$

• Area of the sector without an angle $= \frac{lr}{2}$.

• Perimeter of sector $= 2r + l$

Arc Length of a Sector Formula

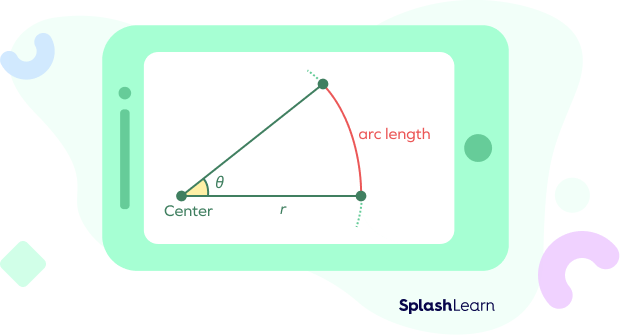
The length of the arc “l” of the sector with angle is given by:

$l = \frac{\theta}{360}\times2\pi r$  …when $\theta$ is given in degrees

$l = \theta r$ …when$\theta$ is given in radians

Facts about Sector of a Circle

• A section or part of a circle involved by two radii with a central angle $90^\circ$ is called a quadrant.

• A section or part of a circle involved by two radii with a central angle of $180^\circ$ is called a semicircle.

• The combination of any two hands (minute hands and hour hands or hour hands and second hands or minute hands and second hands) of a circular analog clock form sectors.

Conclusion

In this article, we learned about the sector of a circle, minor and major sector, the sector formula for area, perimeter and arc length with and without angle. Now, let us look at some solved examples and practice questions.

Solved Examples On Sector of a Circle

1. Calculate the area of the sector.

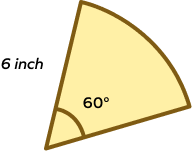
Solution:

The radius of sector $= r = 6$ inches

Angle of sector $= \theta = 60^\circ$

The area of sector $= \frac{\theta}{360^\circ}\times\pi r^2 = \frac{60^\circ}{360^\circ}\times3.14\times6^2 = 18.84$ sq. in.

2. Find the area of a sector of a circular region whose central angle is 3 radians with a radius of 5 feet.

Solution:

The radius of sector $= r = 5$ feet

Angle of sector $= \theta = 3$ radians

If is measured in radians, then

The area of the sector $= \frac{\theta}{2}\times r^2 = \frac{3}{2}\times5^2 =37.5$ sq. feet.

3. Find the central angle of a sector (in degrees) which has a 25 sq. yard area and a radius of 4 yards. Use $\pi = 3.14$.

Solution:

Radius of sector $= r = 4$ yards

Area of sector $= 25$ sq. yards

If is measured in degrees, then

Area of the sector $= \frac{\theta}{360^\circ} \times \pi r^2$

$25 = \frac{\theta}{360^\circ}\times3.14\times4^2$

$\theta = \frac{25\times360}{3.14\times4^2} = 179.14^0$

4. Find the perimeter of the sector shown below.

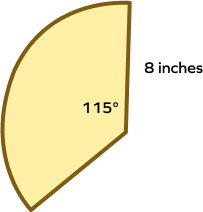
Solution:

The radius of sector $= r = 8$ inches

Angle of sector $= \theta = 115^\circ$

The perimeter of sector $= 2r + \frac{\theta}{360}\times2\pi r$

     $=(2\times8) + \frac{115^\circ}{360^\circ}\times(2\times3.14\times8)$

     $=16 + (\frac{1}{4}\times23.14\times8)$

     $=16 + 12.56$ 

     $=28.56$ in

5. Find the area and perimeter of a sector with a radius of 10 feet and an arc length of 12.56 feet.

Solution:

The radius of sector $= r = 10$ feet

Arc length $= l = 12.56$ feet

Area of the sector without an angle $= \frac{lr}{2} = \frac{12.56\times10}{2}=62.8$ sq. feet

Perimeter of sector $= 2r + l = 2(10) + 12.56 = 32.56$ feet.

6. Find the arc length of a sector having a radius of 5 feet and a central angle of $120^\circ$.

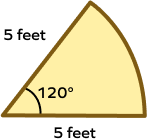
Solution:

The radius of sector $= r = 5$ feet

Angle of sector $= \theta = 120^\circ$ 

The length of the arc “l” of the sector with angle is given by;

$l = \frac{\theta \pi r}{180} = \frac{120\times3.14\times5}{180} = 10.47$ feet

Practice Problems On Sector of a Circle

Frequently Asked Questions On Sector of a Circle