Singleton Set: Definition, Formula, Properties, Examples, FAQs

What Is a Singleton Set in Math?

A singleton set is a set containing a single element. A singleton set is also called a unit set since there’s only one element present in the set. 

In math, a set is a collection of well-defined objects. A singleton set P having only one element p is written as $P = \left\{p\right\}$.

The cardinal number is one, and In sets, cardinality is the total number of elements in a set. Before moving on further, let us first consider the definition of the singleton set.

Singleton Set: Definition

A singleton set can be defined as a set containing only one element. A set is a singleton set if and only if it has only one object. 

Cardinality of Singleton Set

The number of elements in a set is called the cardinality of the set. Thus, the cardinality of a singleton set is 1.

Power Set of a Singleton Set

The power set of a set is the set of all subsets of the given set. The number of subsets of a singleton set is two. One subset is the empty set (∅), and the other is the set itself. Thus, the power set of any singleton set always contains only 2 elements.

Example: Write the powerset of the set $A = \left\{5\right\}$.

Powerset of $A = \left\{5\right\} = P(A) = \left\{∅, \left\{5\right\}\right\}$ 

Properties of the Singleton Set

• A singleton set is a finite set since it has exactly one element.
• A singleton set has a cardinality of 1 since the number of elements in the set is one.
• Since a singleton set has one element, it becomes a subset of any set that has the same element in it. 
• A singleton set containing an element “a” and any set not containing the element “a” are always disjoint sets. 
• Empty set ∅ is a subset of every set. Thus, it is also a subset of a singleton set.
• Empty set and the set itself are the only two subsets of the singleton set.
• The cardinality of the powerset of any singleton set is 2.

Singleton Set: Examples

Let’s look at a few examples of singleton sets.

Example 1: $A = \left\{\text{x : x is a natural number less than} 2.\right\}$

There’s only one natural number less than 2, which is 1.

Thus, A is a singleton set given by $A = \left\{1\right\}$.

Example 2: B is the set of vowels in the word MATH.

In the word MATH, there’s only one vowel, which is “A.”

Thus, $B = \left\{A\right\}$ is a singleton set.

Example 3: P is a set of even prime numbers

2 is the only even prime number.

Thus, $P = \left\{2\right\}$ is a singleton set.

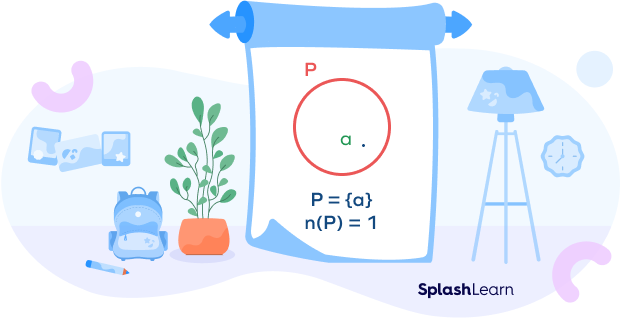
Venn Diagram of a Singleton Set

The Venn diagram of a singleton set is a circle with only one element inside.

Singleton Set vs. Empty Set

Singleton Set	Empty Set
A singleton set contains only one element.	An empty set has no elements.
A singleton set with element x is denoted by $\left\{x\right\}$.	An empty set is denoted by the symbol ∅. It is also expressed as $\left\{\right\}$.
If $A = \left\{a\right\}$, then $n(A) = 1$.	$n(∅) = 0$
Other names are unit set, one-point set.	Other names are null set, void set.
Empty set is always a subset of a singleton set.	Empty set is the only subset of itself.

Is the Zero Set {0} a Singleton Set?

The zero set {0} is a set with “0” as the only element. Thus, it is a singleton set. 

Note that the singleton set {0} is not to be confused with an empty set. An empty set is a set that has no element. It is completely null or void.

{0} ∅

Facts about Singleton Set

Conclusion

In this article, we learned about singleton sets, notation, examples, and their important properties. Let’s solve a few examples and practice problems for better understanding.

Solved Singleton Set Examples

1. Define the set of even perfect squares less than 10. Is it a singleton set?

Solution:

Let E be the set of even perfect squares less than 10.

Perfect squares less than 10 are 1, 4, 9.

The only even perfect square less than 10 is 4.

Thus, $E = \left\{4\right\}$ is a singleton set.

2. How many elements does the set $\left\{x : \text{x is an integer such that 998} \lt x \lt 1000\right\}$ have?

Solution:

The only integer between 998 and 1000 is 999.

$\left\{x : \text{x is an integer such that} 998 \lt x \lt 1000\right\} = \left\{999\right\}$

Thus, the given set has only one element. It is a singleton set.

3. What is the power set of $A = \left\{t\right\}$?

Solution:

$A = \left\{t\right\}$

The power set of the set A or P(A) will be the set of all subsets of A.

The subsets of $A = \left\{t\right\}$ are the empty set and the set itself.

The power set of A will be written as

$P(A) = \left\{∅, \left\{t \right\}\right\}$

4. Is the set $K =  \left\{x : \text{x is a real number such that} x = 9 \right\}$ a singleton set?

Solution:

3 and -3 are the two square roots of 9.

Thus, $K = \left\{3,\; \;-\;3\right\}$ 

K is not a singleton set.

Practice Problems on Singleton Set

Frequently Asked Questions on Singleton Set