SSS (Side Side Side): Definition, Theorem, Similarity, Examples

What Is SSS Theorem (Side-Side-Side Theorem) in Geometry?

The SSS theorem is called the Side-Side-Side theorem. It is a criterion used to prove triangle congruence as well as triangle similarity. However, the terms of the SSS criterion in both the cases are different. 

Congruent Triangles: Two triangles are congruent when they have the same shape and the same size. Corresponding angles and corresponding sides of two congruent triangles are also congruent. We denote the triangle congruence using the symbol ≅.

Similar Triangles: Two triangles are similar when they have the same shape but may differ in size. Corresponding angles of similar triangles are congruent. Corresponding sides of two similar triangles are proportional. We denote the triangle similarity using the symbol .

The SSS theorem helps us to prove the triangle congruence or similarity just using the lengths of the three sides. Other dimensions are not required.

SSS Definition

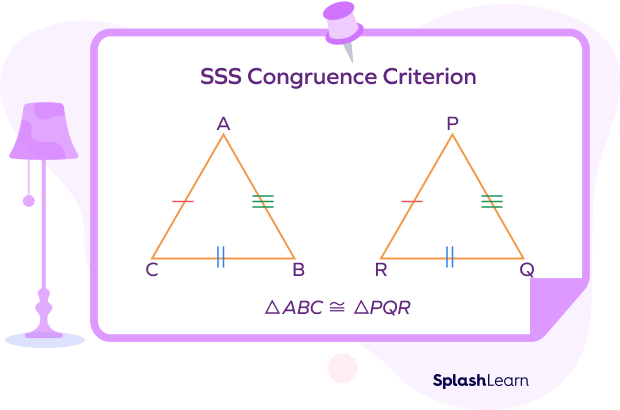
SSS Congruence Theorem: To prove triangle congruence, we use the SSS congruence theorem, which states that when all three sides of a triangle are equal to the corresponding sides of another triangle, and the two triangles are congruent. 

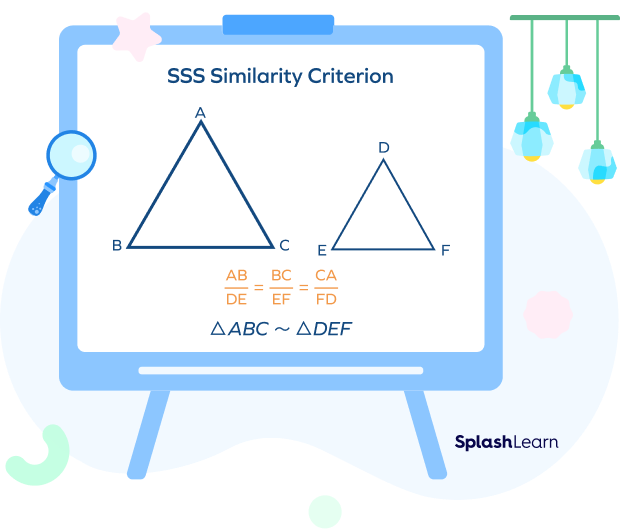
SSS Similarity Theorem: To prove that two triangles are similar, we use SSS similarity criterion, which states that if the ratio of the corresponding sides of two triangles is equal, then two triangles are similar.

SSS Congruence Theorem (SSS Congruence Rule)

Example: Are the two triangles congruent?

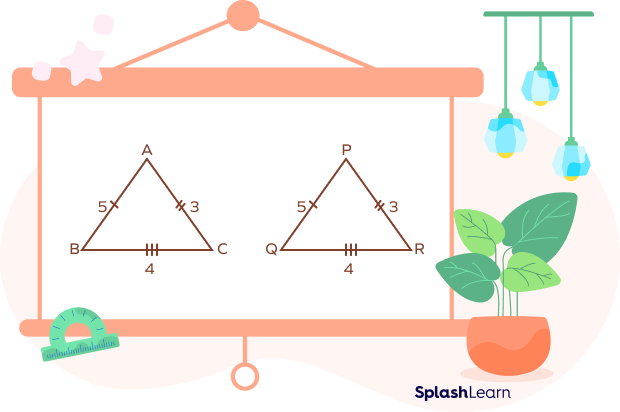
Given:

AB = PQ = 5 units

BC = QR = 4 units

AC = PR = 3 units

Thus, ▵ABC $\sim$ ▵PQR By SSS congruence theorem

SSS Similarity Rule

Example: Are the given two triangles similar by SSS similarity rule?

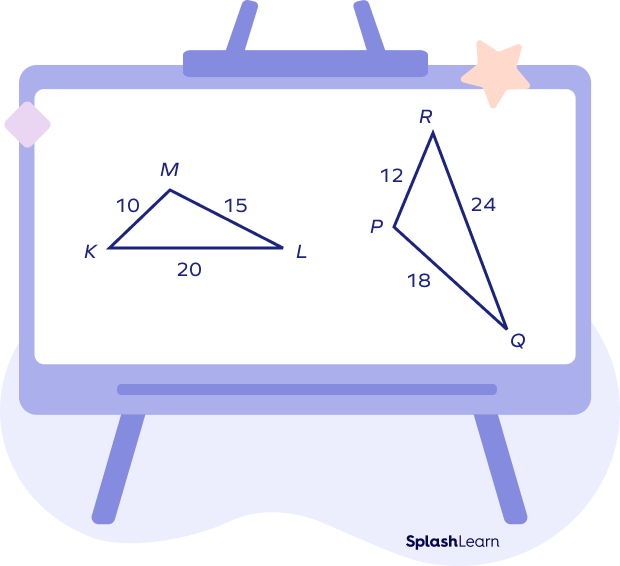
Here,

$\frac{MK}{PR} = \frac{10}{12} = \frac{5}{6}$

$\frac{KL}{RQ} = \frac{20}{24} = \frac{5}{6}$

$\frac{LM}{PQ} = \frac{15}{18} = \frac{5}{6}$

Thus, \frac{KL}{QR} = \frac{MK}{PR} = \frac{ML}{PQ} = \frac{5}{6}$

The corresponding sides are proportional.

Thus, ▵MKL $\sim$ ▵PRQ

SSS Formulas

SSS Congruence Rule: If the three sides of ΔABC are congruent to the corresponding sides of ΔXYZ, then ΔABC ≅ ΔXYZ.

If AB = XY, BC = YZ, and AC = XZ, then ΔABC ≅ ΔXYZ.

SSS Similarity Rule: If the ratio of the corresponding sides of ΔABC and  ΔXYZ is equal, then the  ΔABC ~ ΔXYZ.

If $\frac{AB}{XY} = \frac{BC}{YZ} = \frac{AC}{ZX}$, then ΔABC $\sim$ ΔXYZ.

(Note that when we write the congruence or similarity notation, the order of the vertices is important to identify the corresponding parts.)

Facts about SSS Theorem

Conclusion

In this article, we have learned about the SSS theorem, congruence rule and similarity rule with SSS rule examples. Now, let us practice solving problems on the SAS Theorem.

Solved Examples on  SSS Theorem

1. Prove that ∆ABC and ∆ADC are congruent.

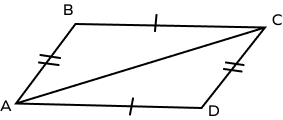
Solution:

In a ΔABC and  ΔADC, 

AB = CD  (given)

BC = AD (given)

AC = AC (Common side)

Thus, by SSS congruence theorem, ΔABC ≅  ΔADC.

2. Are the given two triangles similar?

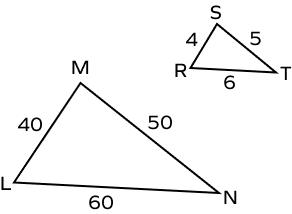
Solution:

Let’s find the ratio of the corresponding sides.

$\frac{LM}{RS} = \frac{40}{4} = 10 : 1$

$\frac{MN}{ST} = \frac{50}{5} = 10 : 1$

$\frac{LN}{RT} = \frac{60}{6} = 10 : 1$

The ratio of corresponding sides is constant.

Thus, the two triangles are similar by SSS similarity rule.

3. Prove that ∆ABC ≅ ∆PQR.

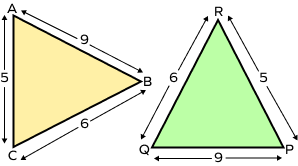
Solution:

AB = PQ = 9

BC = QR = 6

AC = PR = 5

Thus, ∆ABC ≅ ∆PQR by side-side-side congruence theorem.

Practice Problems on SSS Theorem

Frequently Asked Questions about SSS Theorem