Surface Area of Pyramid: Definition, Formula, Examples

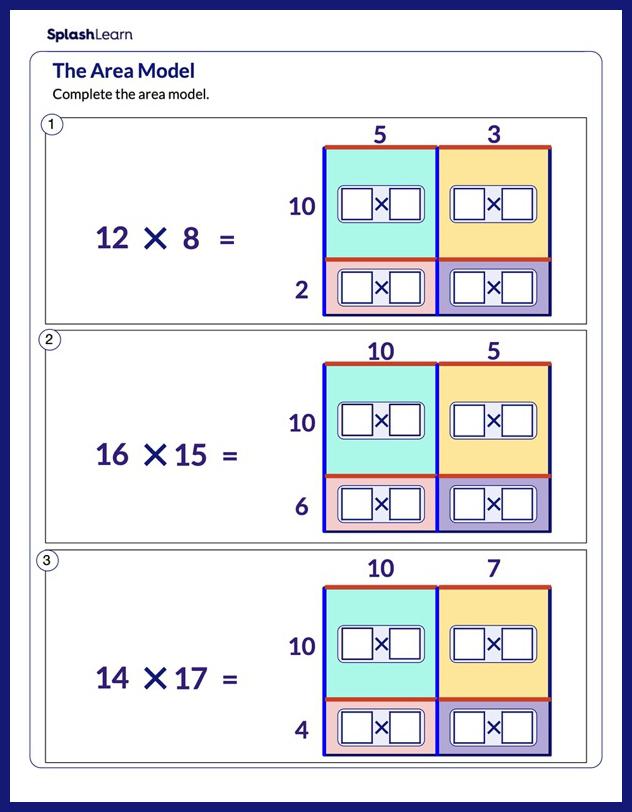
A pyramid is a three-dimensional structure having a polygon as its base and triangular lateral faces. Surface area of a pyramid is simply the sum of all its faces. The pyramids are named after the polygon at its base.

Here’s an image showing a rectangular pyramid and a triangular pyramid.

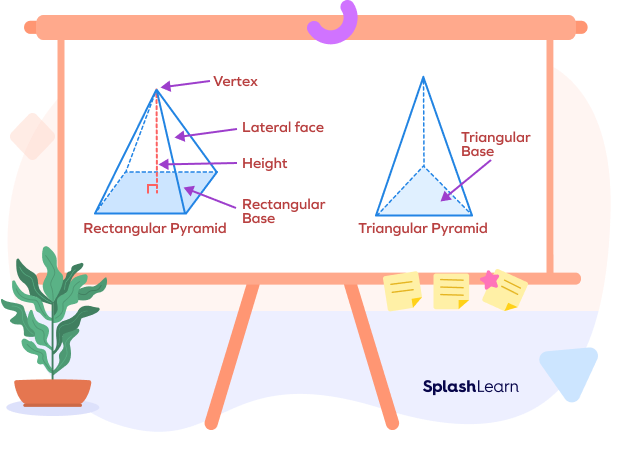
What Is the Surface Area of a Pyramid?

The surface area of a pyramid is the sum of the areas of all faces of the pyramid. Surface area is measured in squared units such as cm², m², in², etc.

Since, all the faces of a pyramid are triangles except for the base, the surface area is calculated by finding the area of the triangular faces along with the area of the base.

Example: If you open up the square pyramid, its net and individual faces will look like this:

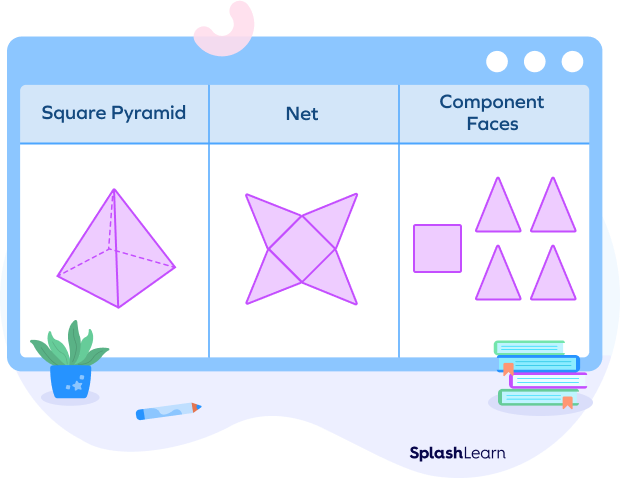
In order to find its surface area, we will add up the areas of four triangular faces and the area of the square at its base.

Surface Area of a Pyramid Formula

There are two types of surface areas.

Total Surface Area (TSA): It refers to the area of all the faces of a pyramid.

The Total Surface area of any pyramid = Area of base + Area of each of the lateral faces

Lateral Surface Area (LSA): It refers to the area of the lateral faces

The Lateral Surface Area of pyramid (LSA) = Area of the triangular lateral faces

Important Note:

The surface area of a regular pyramid $=$ Base Area $+ \frac{1}{2} Ps$

Where, P: Perimeter of the base and s: slant height

Let’s take a look at the formulas for the surface area of different pyramids.

Triangular Pyramid

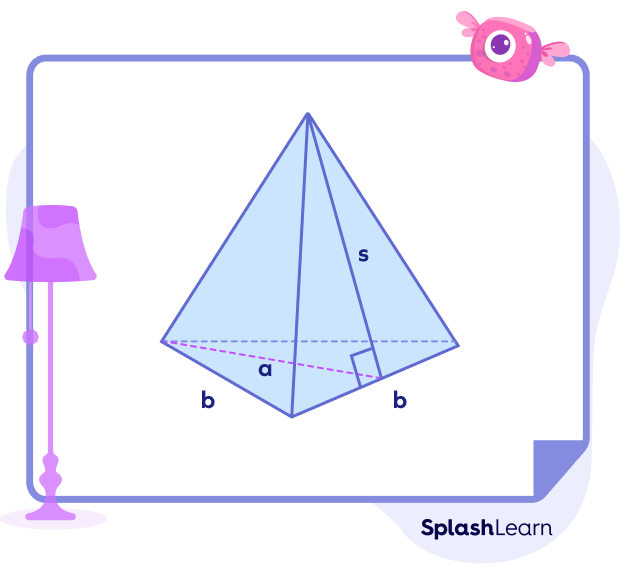
Surface area of triangular pyramid $=$ Base area $+ LSA = \frac{1}{2} ab + \frac{3}{2}bs$

Here, b: side of the base triangle

a: height of the base triangle

s: slant height

Square Pyramid

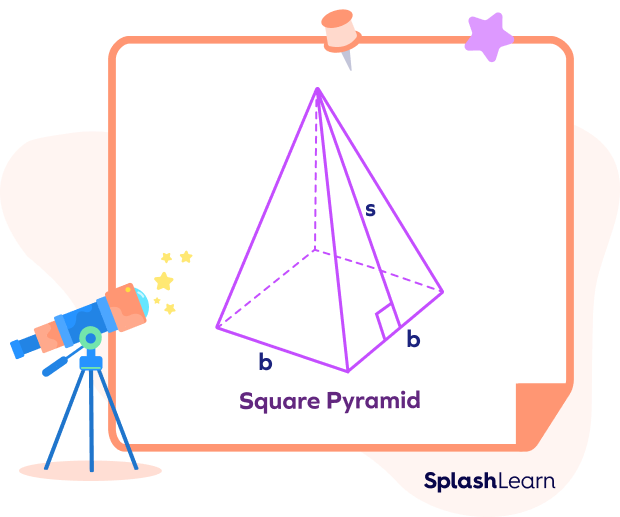
Surface area of a square pyramid $=$ Area of the base $+ LSA = b^2 + 2bs$

Here, b: side of the base-square

s: slant height

Proof of Surface Area of Pyramid Formula

Let us look at the net of a square pyramid. 

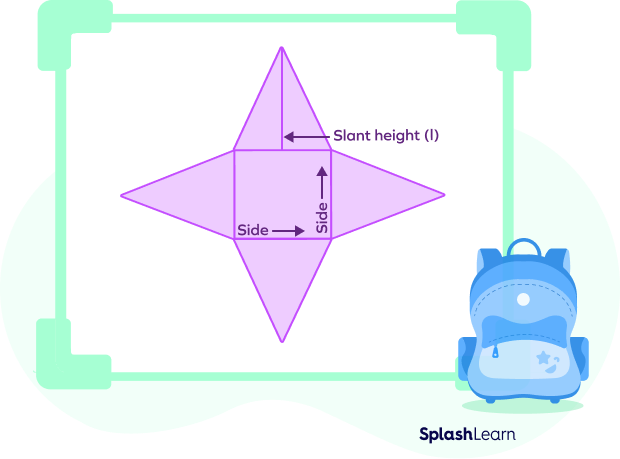
The area of the square at the center (base of the pyramid $= (side)^2 = s^2$

The area of one lateral face $=$ area of a triangle $= 12 \times base \times height

Here, base = side of the square = s and height = slant height (l)

Area of triangle $= \frac{1}{2} \times side \times l$

The area of 4 of these triangles $= 4 \times \frac{1}{2} \times s \times l = 2 \times side \times l$

Total surface area $= 2 \times side \times l +(side)^2$

Hence, the formula for the surface area of a square pyramid is $2\; sl + s^2$.

$s =$ side of the base

$l =$ slant height

Hence, proved.

How to Find the Surface Area of a Pyramid

Step 1: First of all find the measurement of the base. If it is a rectangle, then we find the length and width. If it is a square, then we find the length of the side. 

Step 2: Find the area of the base. This area is known as “A.”

Step 3: Then we measure the slant height. This distance is known as “l.”

Step 4: Now we put the values in the surface area of a pyramid formula. 

Surface Area of a Pyramid with Altitude

The surface area of the pyramid can also be calculated if the altitude base length is given. 

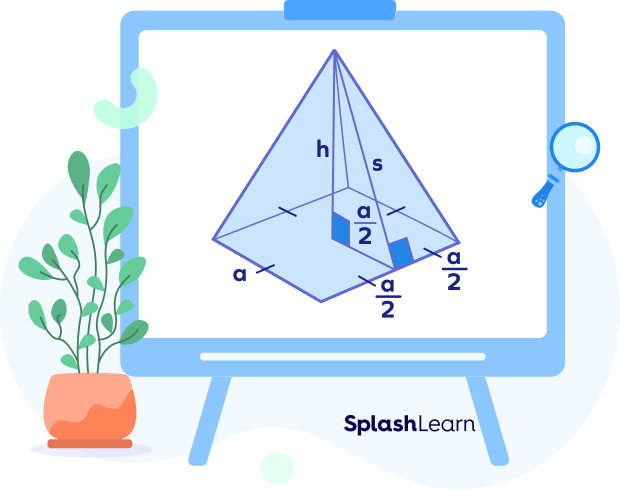
The slant height can be calculated using the Pythagoras theorem as

$(slant\; height)^2 = (\frac{a}{2})^2 + (Altitude)^2$

$s^2 = (\frac{a}{2})^2 + h^2$

Using this value, the surface area of the pyramid can be calculated.

Conclusion

In this article, we learned about the surface area of square pyramids. We saw the formula and ways to calculate the surface area of square pyramids. Let’s now solve a few examples on the surface area of a pyramid and do some practice problems to understand it better. 

Solved Examples on Surface Area of Pyramid

1. A square pyramid has base dimensions of $75\; ft \times 75\; ft$ and its slant height is around 500 ft. Calculate its surface area.

Solution:

Base Area $= 75 \times 75 = 562,5$ square feet.

The slant height of the pyramid is $l = 50\; ft$.

Surface area of pyramid $= (2 \times s \times l) + s^2$

$=(2 \times 75 \times 50) + 5625$

$= 7500 + 5625$

$=13125\; sq.\; ft$

2. The base of a square pyramid has dimensions $10\; units \times 10\; units$ and the slant height is 4 units. What is the area of the canvas she will require to build the tent?

Solution:

The base area $=$ Area of a square $= A = 10 \times 5 = 50$ square units.

The slant height of the tent is $l = 4$ units.

The area of canvas to build the tent using the surface area of pyramid formula is,

Surface area of pyramid $= 2 \times s \times l + Base Area$

$= (2 \times 10 \times 4) + 50$

$= 80 + 100$

$= 180\; sq.\; units$

3. For the triangular pyramid, the side length of the base is 7 cm and height of the base is 6 cm. Find its surface area if the slant height of the pyramid is 16 cm.

Solution:

Given the side length of the base $= 7\; cm,\; height = 6\; cm$

Slant height $l = 16\; cm$

Surface area of pyramid $= \frac{1}{2} \times b \times h + \frac{3}{2} \times b \times l$

Where, s = side of the base

$l =$ slant height,

$b =$ base length,

$h =$ height of the base

So, surface area of pyramid $= (\frac{1}{2} \times 7 \times 6) + (\frac{3}{2} \times 7 \times 16)$

$= 21\; cm^2 + 168\; cm^2$

$= 189\; cm^2$ 

The surface area of the given pyramid is $189\; cm^2$.

4. What is the slant height of a pyramid if the surface area is $560\; in^2$ and side length is 14 inches.

Solution:

Surface area of a pyramid $= 560\; in^2$ 

Side length $s = 14$ inches

Surface area of pyramid $= (2 \times s \times l) + s^2$

$\Rightarrow 560 = 2 \times 14 \times l + 14^2$

$\Rightarrow 560 = 28\;l + 196$

$\Rightarrow 28\;l = 560\;-\;196$

$\Rightarrow l = 364/28$

$\Rightarrow l = 13$

The slant height of the given pyramid is 13 inches.

Practice Problems on Surface Area of Pyramid

Frequently Asked Questions on Surface Area of Pyramid